УРАВНЕНИЯ ПРОСТРАНСТВЕННОГО ДВИЖЕНИЯ САМОЛЕТА В БЕЗРАЗМЕРНОМ ВИДЕ

В том случае, когда необходимо рассматривать управля­емое движение самолета при полете с относительно малыми углами атаки, которое может сопровождаться развитием больших угловых скоростей, в уравнениях движения необходимо сохранить не­линейные члены, содержащие произведения угловых скоростей. При рассмотрении уравнений движения, записанных относи­тельно главных осей инерции, необходимо учитывать, что угол атаки (а), в функции которого определяются аэродинамические характеристики самолета, обычно отсчитывается от оси стро­ительной горизонтали самолета. В связи с этим при определении величины Vy но формуле (1.5) необходимо в качестве угла атаки рассматривать величину

% = a — J — фг, (2.1)

где фг — угол между строительной горизонталью самолета, от которой отсчитывается аэродинамический угол атаки, и главной осью инерции ОХ (фг > 0, когда для совмещения положительной полуоси ОХ со строительной горизонталью ее необходимо повер­нуть по часовой стрелке относительно оси 0Z).

Подставляя соотношения (1.5) в уравнения движения (1.3) И (1.11) с учетом выражений (1.13) и производя необходимые преобразования, для общего случая горизонтального полета с пе­ременной скоростью V и малых величин аир, получим следующую систему дифференциальных уравнений:

— a — j — со2 — рсо*—— (фг а) = Y0 + Yaа Кфф———————— — cos ft cos у;

(Ьг + AtojOy = Мг0 + Мг а + Мг°Ч + Aff а + Л??<р; (2.2)

Р а>у -] у — р (£>х (фг + а) = Z? р — j — Z6la8H — ф- -у — cos О sin у;

~~ Ba>xi! dz = Мур — f — Муу(ду — f — Мух(дх -[- Му11бн -{- Муэ8э;

(Ьх 4- Со)у(о2 = Мхр 4~ Мххсох 4~ МхуЫу 4~ Мхнбн 4~ Мхэ83; (2.3) У = — (Сха—СрУ^ — ё Sin 0-

В системе уравнений (2.2) и (2.3) точкой обозначено дифференци­рование по времени, а аэродинамические силы и моменты пред­ставлены основными линейными членами разложения в ряд по параметрам движения самолета. При этом приняты следующие обозначения:

CyoqS ш mV	mzGqSl. /г ’
-О).
м2г =

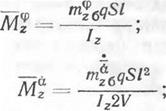
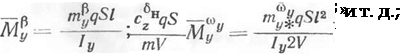(2.4)

	rnxqSl ~ ІХ ’	1! 1^	mx£qSi2 1х 2V	И т. д.;
м1п	mfysi ~ 1у ’	мУ =	tn^zqSl "	и т. д.;
_ V	71х : В-	lz—-	; C =	^2 — ^

X

Для получения большей общности результатов, особенно при аналитических оценках, в ряде случаев уравнения движения самолета целесообразно преобразовать к безразмерному виду. Для приведения уравнений к безразмерному виду введем следу­ющие переменные:

масштаб времени тт;

безразмерные угловые скорости со*, сор, (о2; безразмерные моменты инерции самолета iX9 iyj iz

(2.5)

Отметим, что параметры тт, pt и коэффициент / 2V, используемый

при вычислении (0(*, Z), совпадают с аналогичными параметрами,

используемыми при приведении уравнений бокового движения к безразмерному виду. При преобразовании уравнений продоль­ного движения к безразмерному виду значения р и со2 обычно вы­числяются с использованием величины средней аэродинамической хорды (ЬА) в качестве характерного размера, что следует иметь в виду при анализе полной системы уравнений движения. По этой же причине необходимо производные аэродинамических коэффи-

СС й 1

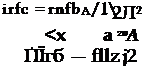циентов т2б, tnzб и т. д. определять с помощью следующих фор­мул:

Используя соотношения (2.5), преобразуем уравнения (2.2) к безразмерному виду для полета самолета на постоянной высоте (р = const). Изменение скорости полета при горизонтальном полете, когда sin 0 ~ 0, описывается уравнением (2.3), в котором величину (сха — сР) для упрощения анализа примем постоянной. Введем безразмерное время т с помощью следующего дифферен­циального соотношения:

где величина тт является переменной вследствие изменения ско­рости полета V. При проведении преобразований необходимо учитывать следующее правило дифференцирования:

(2.8)

ГДЄ COj — C)(x, y,z)‘

В результате простых преобразований с учетом соотношений (2.7) и (2.8) получим уравнения движения самолета в безразмер­ном виде:

«’ — = [ ~~Г+ 2 "] + Ф +

2gx? L

-j-— cos # cosy;

^ — f AiunxWy = m?6a + + °* 2 °p jex, + /га«б~- + m\

(2.9)

+ + габн8 + тбэб —

1 Г/* X * у н * і/ э*

«і + Сцс^о* = + (т“| + со* +

где X =

В дальнейшем нижний индекс (*) у производных га**, ту% и т. д. будет опускаться для сокращения записи. В системе урав­нений (2.9) приняты следующие обозначения:

Удобство безразмерной формы уравнений состоит, в частности, в том, что, не решая уравнений, можно сделать некоторые общие выводы о свойствах их решений. В частности, единственным параметром в системе уравнений (2.9) после отбрасывания грави-

27

тационных членов, зависящим от режима полета, является вели­чина (її. Величина р определяется высотой и не зависит от скорости полета. Отсюда следует вывод о том, что качественная картина движения самолета при действии возмущений и при управлении зависит только от высоты полета и не зависит от скорости. Основ­ное влияние скорости полета выражается в изменении масштаба времени. Например, при аГвП = const, от скорости полета за­висят частота колебаний и время затухания, но не зависят устой­чивость движения, величина декремента затухания, количество и вид особых точек системы уравнений движения и т. д. (все это справедливо с единственной оговоркой о том, что в окрестности рассматриваемых режимов полета аэродинамические коэффици­енты мало зависят от скорости и числа М полета). Уравнения (2.9) после отбрасывания гравитационных членов являются нелиней­ными уравнениями с постоянными коэффициентами даже для слу­чая движения самолета с переменной скоростью (если сха — сР = = const). При этом переменность скорости проявляется в изме­нении демпфирования благодаря наличию коэффициента (сха — сР) и в изменении масштаба времени. При переходе к размерному времени необходимо пользоваться следующей зависимостью t от т:

<2">

О о

Для получения зависимости между t и т в явном виде преобразуем уравнение (2.3) к новой переменной т:

= (2.12)

Проинтегрировав уравнение (2.12) при сх — сР = const, получим

V = У0ехр (— т. (2.13)

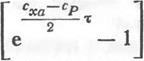И, наконец, подставляя (2.13) в (2.11) и производя интегрирование, получаем формулу для зависимости t от т:

Легко проверить, что при (сха — сР) -> 0 это выражение в пределе переходит в тождество t = ттт0. Из системы уравнений (2.9) непосредственно видно, что разгон самолета (полет при сР > сх) увеличивает демпфирование, т. е. действует стабилизирующе, а торможение (сР < сха) — дестабилизирующе, т. е. при полете

с уменьшающейся скоростью эффективное демпфирование умень­шается.

Ввиду того, что в дальнейшем будут анализироваться уравне­ния движения в безразмерном виде при постоянной скорости полета, когда сха = сР, перепишем их еще раз, учитывая сделан­ные ранее замечания и опустив гравитационные члены:

а’ — [ш2 + ироц. =——- j — а — Асу

^а’

СОг — f — АШ>х(Х>у — /Яг(-СС -|- /ЙгбСОг -( — tt’ -j — ІПгСіЧ

г

_ ср

Р’ — И®^ — И®.< (а + ф) = -f — Р + Асг; (2.14)

o)j, — В(і(охшг = /га^р -(- т’уиЫу + ту<ох

(0Х + сШу(0г = т9х Р + тхх(йх + тхуа>у + А тх.