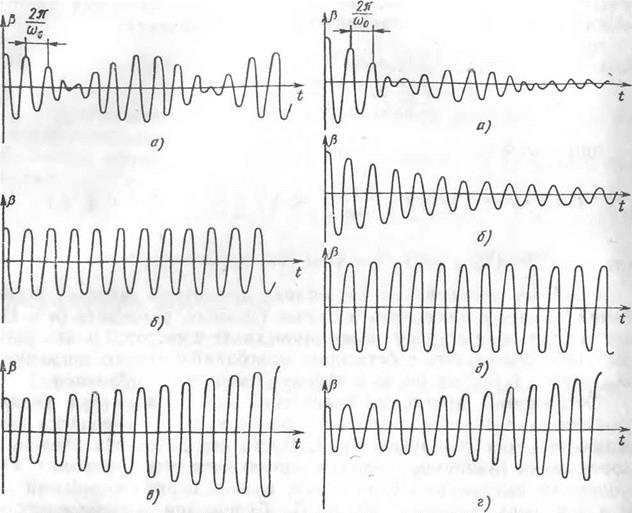
ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС ПРОДОЛЬНЫХ Й БОКОВЫХ КОЛЕБАНИЙ

Как известно [13], основные характеристики бокового движения, такие как частота колебаний и декремент затухания, могут зависеть от величины угла атаки самолета, однако малые вариации угла атаки оказывают несущественное влияние на боко­вое движение самолета так же, как малые вариации параметров бокового движения не влияют на угол атаки. Картина существенно изменяется, если выполняются определенные соотношения между собственными частотами продольных и боковых колебаний. В этом случае энергия продольных колебаний передается боковым ко­лебаниям и может реализоваться параметрический резонанс [29, 48]. При этом роль переменного параметра играет угол атаки, который изменяется с частотой продольных колебаний, а пере­менной, колебания которой при этом возбуждаются, является угол скольжения самолета. При слабом демпфировании движения, что может быть при полете самолета на большой высоте, вслед­ствие параметрического резонанса возможно интенсивное нара­стание амплитуды боковых колебаний, т. е. практическая потеря устойчивости движения самолета.

В работе [29] рассмотрены условия реализации параметри­ческого резонанса такого типа и влияние аэродинамических характеристик самолета и условий полета на возможность его возникновения.

Анализ строится на рассмотрении упрощенных уравнений короткопериодического продольного и бокового движений, ис­пользуемых при анализе быстрых составляющих возмущенного движения.

Рассматривая движение в полусвязанной системе осей коорди­нат, можно определить в этой системе координат угловую ско­рость £2^, Qy летательного аппарата и производные аэродинами­ческих моментов. При преобразовании уравнений возмущенного движения будем пользоваться обозначениями, приведенными в табл. 7.1. С учетом этих обозначений боковое движение само­лета будет описываться уравнениями

Р = Qq cos Да + Qy sin Да + Zp|3;

S2V = 0VP + + M^QV.

Таблица 7.1 Формулы для вычисления параметров бокового движения самолета в полусвязанной системе координат
Угловые скорости вращения относительно полусвязанной системы координат	Эффективные коэффициенты аэродинамической устойчивости в полусвязанной системе координат
— (ду cos а{) — f — сох sin а0 Qy ~ (Dx cos а0 — (Оу sin а0	Gp — М^ cos a0 + М ^ sin a0 ду = Лї£ cos a0 — МР sin a0
Демпфирующие моменты относительно связанной системы координат, возникающие при вращении самолета относительно полусвязанной системы координат
—Q і — со —го МуФ = Му У cos а0 — f Му у sin а0 М^У = МСуХ cos а0 — М^у sin а0	Мх$ = Мхх sin а0 + М™у cos a0 М^У = Мхх cos a0 — М™у sin а0
Эффективные демпфирующие моменты в полусвязанной системе координат
cos а0 + мУ sin а0 — Q —й — Q = МуУ cos aG МХУ sin а0	Му^ = МХУ cos a0 — Му^ sin ос0 — Q ——— Q —————— Q МуУ = МХУ cos a0 — МуУ sin aQ

Изменение угла атаки самолета сказывается на колебательной составляющей бокового движения. Наиболее благоприятные усло­вия для возникновения резонанса имеют место в случае малого демпфирования движений. При малом демпфировании бокового движения приближенно выполняется соотношение между состав­ляющими Qv, угловой скорости:

"ЦТ ^ "fy = Ипр (а°) = const — (7-2)

Введем обозначения:

—орК); (7.3)

ар (а) = —(оро (1 + Да),

где сор0 — приближенное выражение для частоты боковых ко­лебаний;

— приближенное значение коэффициента демпфирования бо­ковых колебаний.

С учетом обозначений (7.2)—(7.5) уравнения (7.1) приводятся к виду

Р — (1 ~Ь ^пр Д°0 2^fi; (7.6)

6* = —©|(1 + К Аа) р — Ц. (2?р — f Zp).

Введем новую переменную

u{t) = (l + Хпр Аа)~1/2 р (/). (7.7)

Переменная и (t) приближенно будет определяться как ре­шение уравнения

Если считать демпфирование продольных колебаний пренебре­жимо малым, то уравнение продольного движения можно запи­сать в виде

Да + соао Да = 0. (7.9)

Амплитуда боковых колебаний может или нарастать, или оставаться ограниченной — в зависимости от соотношения между частотами боковых (сор0) и продольных (соа0) колебаний.

При h = 0 и Аа Дашах cos сoa0t уравнение, описывающее боковое движение, принимает вид

й -j — со| (1 + a cos о)(хо0 и •— 0, (7.10)

где

О = (к + хпр ^np ‘ 2^2 j ^ашах — (7-Н)

Резонансные значения частот, соответствующие неустойчивым решениям уравнения (7.10), могут быть определены с помощью диаграмм устойчивости и неустойчивости решений уравнения

55

Матье (рис. 7. 1). В случае а | 1 области резонансных частот

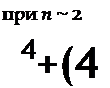можно определить из приближенных соотношений: при п Ж 1

где п =

Наиболее интенсивное нарастание амплитуды боковых коле­баний может происходить в случае главного резонанса (п = 1), когда колебания по углу атаки происходят с частотой в два раза большей, чем частота собственных колебаний бокового движения: ша0 = 2сор0. С ростом числа п эффект резонанса ослабляется.

Остановимся кратко на физических причинах потери устой­чивости самолета при развитии параметрического резонанса для наиболее простого случая п= 1. Пусть под действием внешнего возмущения (например, порыва ветра) начались колебания са­молета по рысканию и углу атаки, причем период колебаний по а в два раза меньше, чем по р. Будем для определенности рассматривать случай, когда степень устойчивости самолета по рысканию убывает при возрастании угла атаки. Тогда при оп­ределенном соотношении фаз колебаний по а и р максималь­ные значения Да(Да>0) будут совпадать с максимумами и минимумами р, т. е. в моменты, когда р приближается к своим экстремальным значениям, степень устойчивости убывает, что и приводит к возрастанию ампли­туды колебаний.

Можно показать, что ширина полосы резонансных частот, а сле­довательно, и вероятность реализа­ции резонанса, с ростом п сущест­венно уменьшается. Таким образом, в случае | а ] <С 1 имеет смысл рас­сматривать только первые области неустойчивости (п — 1,2).

На рис. 7.2 показан качествен­ный характер изменения р в случае

Рис. 7.1. Приближенные области устойчи­вости решений уравнений Матье

Рис. 7.2. Зависимость вида движения от соотношения параметров при отсут­ствии демпфирования продольных и боковых колебаний:

 

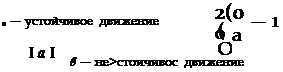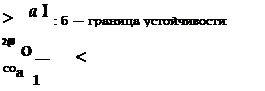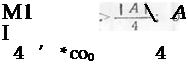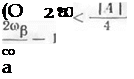Рис. 7.3. Зависимость вида движения от параметров при наличии демпфирования боковых колебаний:

главного резонанса в зависимости от того, попадает соотноше­ние частот боковых и продольных колебаний в резонансную область или нет.

Демпфирование боковых колебаний приводит к тому, что часть энергии колебаний по углу атаки, которая передается бо­ковому движению, рассеивается. Если демпфирование достаточ­
но эффективно, то параметрического резонанса вообще не будет.

Можно показать также [29], что демпфирование сужает по­лосу резонансных частот. В частности, при выполнении нера­венства или, что то^же самое

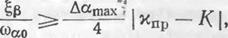(7.13)

области неустойчивости исчезают.

Таким образом, неравенство (7.13) может служить достаточ­ным условием отсутствия параметрического резонанса продоль­ных и боковых колебаний самолета. Качественный характер изменения р (t) при наличии демпфирования в случае главного резонанса [показан на рис. 7.3.

Так как величина |р/(оа0 зависит от условий полета и опре­деляется главным образом плотностью атмосферы, то с помощью соотношения (7.13) можно оценить высоту полета, ниже кото­рой параметрический резонанс в движении самолета не мо­жет быть реализован. Отношение Ысоа0 можно представить в виде

I Р

где зависит только от аэродинамических характеристик са­молета.

Если выполняется неравенство

(7.14)

то движение самолета [устойчиво. Для типичных характе­ристик современного маневренного самолета из этого условия следует, что параметрический резонанс возможен только на высотах полета Н > 15 км, т. е. практически маловероя­тен.

Если продольное движение самолета демпфируется, то коле­бания по углу атаки с течением времени затухают:

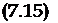Да = Датахе la‘ cos юа0і.

ЁзакмоДейстьие продольного и бокового движений

Характер боковых колебаний будет определяться уравнениями вида (7.8) или (7.10), только в этих уравнениях а — функция вре­мени.

Очевидно, что условия возникновения резонанса с некото­рым приближением будут аналогичны условиям, полученным ранее. Характер бокового движения при малых £а представляется следующим образом.

Амплитуда боковых колебаний нарастает до тех пор, пока выполняется резонансное соотношение между частотами. В не­который момент времени (поскольку а (t) убывает) резонансное соотношение нарушается. Начиная с этого момента, амплитуда боковых колебаний перестает нарастать. Если боковые колеба­ния демпфируются, то амплитуда колебаний по р убывает. Если в начальный момент времени резонансное соотношение между частотами не выполняется, то колебания по углу атаки прак­тически не сказываются на боковом движении. Более подробно особенности движения самолета при резонансных соотношениях собственных частот продольных и боковых колебаний излагаются в работе [29]. Приведенные материалы показывают, что реали­зация параметрического резонанса на практике маловероятна, поскольку требуется одновременно вполне определенное соотно­шение частот и пренебрежимо малое демпфирование продольных и боковых колебаний.