НЕКОТОРЫЕ СООБРАЖЕНИЯ О МЕТОДАХ ПОНИЖЕНИЯ ПОРЯДКА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОСТРАНСТВЕННОГО ДВИЖЕНИЯ САМОЛЕТА

Одним из наиболее распространенных и эффективных методов приближенного анализа задач динамики полета является использование таких упрощающих допущений, которые позво­ляют свести задачу к анализу дифференциальных уравнений не высокого порядка. Понижение порядка системы дифференциаль­ных уравнений, описывающих движение самолета, основывается на одном из двух приемов:

— разделение движений системы на медленные и быстрые;

— разделение уравнений на подсистемы в связи с малой взаим­ной зависимостью параметров, входящих в каждую из подсистем.

Иллюстрацией использования первого приема понижения порядка дифференциальных уравнений является разделение урав­нений продольного движения на уравнения длиннопериодического и короткопериодического движения [13]. В качестве примера второго способа можно назвать разделение уравнений простран­ственного движения на уравнения продольного и бокового дви­жений.

В настоящей книге широко будут использоваться при прибли­женном анализе приемы понижения порядка исследуемых уравне­ний. В связи с этим рассмотрим соображения, лежащие в основе таких приемов.

Метод разделения движений на медленные и быстрые изложен в целом ряде работ [9, 18, 16, 45 и др. ] и заключается в следу­ющем [18]. Пусть движение исследуемой автономной системы описывается системой нелинейных уравнений, записываемой в виде

99

где Ті — постоянные, имеющие размерность времени, сокращенно называемые постоянными времени.

Возможность разделения движений системы на быстрые и медленные возникает тогда, когда в системе (12.1) постоянные времени имеют различный порядок. Например, если таких групп постоянных времени две, то система записывается в виде

Ті (Л-1( . . хъ уъ. . уч); і = 1, . — к (12.2)

nTj = gj (*i, . . *ь У к • • •. yvY, / = 1, • • v. (12.3)

где h + v = п Ті, Tj — величины одного и того же порядка; е — малое отвлеченное число.

При этом предполагается, что правые части уравнений (12.2) и (12.3) не зависят от є и средние значения |/* | и | gj | имеют один и тот же порядок.

Из уравнений (12.2) и (12.3) видно, что переменные xt изменя­ются медленнее, чему* (так как производныеdxjdt—малы). Рассма­тривая быстрые изменения у и будем считать величины Хі постоян­ными, т. е. будем их рассматривать как параметры. Состояния равновесия быстрых движений будут решениями системы урав­нений

gj(xl9 . . ХЪ уъ. . ., у%) = 0, (12.4)

т. е. Уз = УЛхъ • хК). (12.5)

В рассматриваемых задачах, функции (12.5) однозначны. Состоя­ния равновесия (12.5) будут устойчивы, если все корни харак­теристического уравнения быстрых движений, линеаризирован­ных относительно этих состояний равновесия, имеют отрицатель­ные действительные части. Если это условие выполняется при всех yjy определяемых (12.5), то уравнения (12.3) можно заменить уравнениями (12.4), т. е. можно пренебречь малыми постоянными времени eTj.

Исследование получающейся упрощенной системы

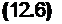Ті ^ /х (-^і * • • •» > Уі» • • • > У) у

Q == gj (-Vi» • * •» Уі» • • •» У)

дает правильный ответ на вопрос об устойчивости исходной си­стемы (разумеется при достаточно малом в), но, во-первых, только по отношению к возмущениям, совместимым с системой (12.6), т. е. таким, при которых изображающая точка в начальный мо­мент лежит на гиперплоскости, определяемой уравнениями (12.5), и во-вторых, если система (12.6) есть грубая система.

Рассмотрим теперь вопрос об устойчивости исходной системы но отношению к возмущениям совместимым с системой (12.2, 12.3), т. е. таким, при которых изображающая точка в начальный момент времени не лежит на гиперповерхности (12.4). Другими словами, рассмотрим устойчивость быстрых координат «в боль­шом», предполагая, что условие их устойчивости «в малом» вы­полнено. Исследовав устойчивость по координатам yjt считая xt постоянными, получим область устойчивости в пространстве ко­ординат ylt yv (вопрос о практическом построении этой области не затрагиваем), которая будет изменяться при измене­нии координат которые играют в данном случае роль пара­метров. Следовательно, можно построить область устойчивости в п-мерном пространстве параметров и координат

xi, —» » У» • • • yv» (12.7)

которую обозначим через Gy.

Аналогично, рассматривая уравнения медленных движений и считая, что для быстрых движений удовлетворяются уравнения установившихся движений, т. е. рассматривая уравнения (12.6), можно построить область устойчивости Gv по координатам

хъ …, х%. (12.8)

Пусть теперь

— суть начальные возмущения координат. Обозначим через А1/у Av начальные положения изображающей точки в пространствах

(12.7) и (12.8), соответственно, определяемые начальными коорди­натами из строки (12.9). Система будет устойчива по отношению к возмущениям (12.9), если точки Ауу Ах будут находиться соот­ветственно в областях Gy и и неустойчива, если хоть одна из этих точек будет находиться вне соответствующей области. Если, например, точка А не лежит в области GXi то неустойчивость проявится в первую очередь в изменении координат хІУ а потом распространится на другие координаты, а если Ау окажется вне Gyy то неустойчивость начнет проявляться с изменения коорди­нат Уі. Пусть точки Ау, Ах находятся соответственно в обла­стях Gyy Gx. Тогда изображающая точка, начав свое движение из Ау за малое время zt попадает в малую окрестность гиперпо­верхности (12.4) вследствие быстрого изменения координат у$. Переменные Хі за это время изменятся мало, после чего начнется ее медленное движение к состоянию равновесия (изменение пере­менных Хі).

Все предыдущие рассуждения верны при достаточно малых є. Этим значениям є соответствуют определенная топологическая структура фазового пространства, которая будет сохраняться при

увеличении е, пока эта величина не достигнет некоторого значе­ния е1э при котором произойдут первые изменения топологии фа­зового пространства, например, изменение типа какого-нибудь из состояний равновесия. Число ех называется первым бифурка­ционным значением в. Очевидно, что изложенные ранее построе­ния будут давать качественно верные результаты, если є < elf и заведомо неверные, если 8 > е±. Однако вопрос о малости пара­метра 8 и при выполнении условия 8 єх не может быть решен только из общих математических соображений: существенную роль здесь играют требования, диктуемые конкретной задачей. Из сказанного вытекает некоторая условность понятия малого параметра, который численно может быть совсем не мал, если в рассматриваемой задаче єх не есть малая величина, а условия задачи позволяют довольствоваться только качественной карти­ной фазового пространства. В настоящей книге последние сообра­жения будут широко использоваться для получения качествен­ного представления о фазовом пространстве, сведения о котором при необходимости могут быть уточнены численными расчетами.

Рассмотрим второй случай,^ когда разделение уравнений на подсистемы возможно в связи с малой взаимной зависимостью параметров, входящих в каждую из подсистем. Этот случай широко распространенного в практике исследования возмущен­ного и управляемого движения самолета с использованием урав­нений изолированного продольного и бокового движений. Такое разделение уравнений является приближенным и область его применения нуждается в обосновании. Материалы, приведенные в настоящей книге, позволяют сформулировать некоторые оценки допустимости таких упрощений.

Нетрудно показать [13], что выделение уравнений продоль­ного движения из общих уравнений пространственного движения при исходном горизонтальном полете самолета, является строгим, т. е. выполняется точно независимо от амплитуд изменения пара­метров продольного движения. В то же время, выделение уравне­ний бокового движения в тех же условиях является приближен­ным и справедливость такого упрощения необходимо обосновы­вать. Кроме этого, в ряде случаев возникает задача исследования продольного движения самолета в процессе более сложного исход­ного движения, например заключающегося во вращении самолета по крену. В этом случае весьма заманчиво исследовать движение, рассматривая значительно более простые, чем в общем случае, уравнения продольного движения.

Во всех перечисленных случаях упрощение исследований до­стигается путем перехода к приближенным уравнениям и, следо­вательно, приводит к появлению определенных ошибок в расче­тах. Перекрестные связи уравнений продольного и бокового дви­жений могут иметь либо линейный, либо нелинейный характер.

Примерами линейного взаимодействия являются влияние гироско­пического момента двигателя, некоторые зависимости аэродина­мических характеристик от параметров движения. Нелинейными перекрестными связями являются, например, связи через инер­ционные моменты, степень воздействия которых на движение самолета нелинейно зависит от амплитуды движения.

При решении вопроса о разделении уравнений на уравнения продольного и бокового движения не всегда необходимо, чтобы параметры выделяемых уравнений не зависели от изменения параметров, описываемых остальными уравнениями. Когда такая зависимость имеет односторонний характер, т. е., например, параметры уравнений бокового движения зависят от парамет­ров продольного движения (а), а обратной зависимости нет, то и в этом случае для ряда задач уравнения могут быть успешно разделены. При этом, если уравнения бокового дви­жения имеют устойчивые решения при величинах а в диапазоне

(%i < а < ос2,

то решения сохраняют устойчивость практически при любых изме­нениях а из этого диапазона. Исключение может составить дви­жение, когда a (t) является периодическим незатухающим про­цессом. В этом случае при некоторых значениях параметров само­лета возможна потеря устойчивости бокового движения вследствие параметрического резонанса. Примеры таких решений были приведены в гл. 2.

Перекрестные связи типа гироскопического момента двигателя являются линейными и их относительный эффект постоянен не­зависимо от амплитуды движения; при малых амплитудах он мал, а при больших — велик. В связи с этим, необходимость учета таких связей решается в зависимости от конкретной задачи. Иной характер влияния у нелинейных связей, например, у инерцион­ных перекрестных связей. Их влияние изменяется пропорцио­нально квадрату амплитуды, поэтому они могут быть несуще­ственны при малых амплитудах движения, но могут оказывать определяющее влияние при увеличении амплитуды. Приближенно можно считать, что удельный вес перекрестных инерционных связей уравнений определяется соотношением величин угловой скорости крена и меньшей из частот собственных продольных либо боковых колебаний. При этом влияние инерционных момен­тов сказывается, в первую очередь, на движении с меньшей соб­ственной частотой колебаний и выражается как в изхменении ампли­туды, так и частоты колебаний получаемого решения. Такие изменения приближенно могут быть оценены на основе анализа параметров установившегося движения. Соответствующие зави­симости могут быть рассчитаны с использованием формул, которые приводятся в табл. 9.1. Полученные значения для установившихся величин параметров движения достаточно полно характеризуют

103

свойства движения и по ним можно оценить возможность разде­ления уравнений. Такое разделение возможно в том случае, когда сохраняется линейность зависимостей от со* по всем параметрам движения в окрестности соЛ — — 0. Как только эта зависимость становится нелинейной, это является признаком существенного влияния нелинейного взаимодействия движений. Однако такой путь в общем случае достаточно громоздок, в связи с чем далее формулируется более простой, но грубый способ оценки. Можно показать, что частота (о*) и амплитуда (ф*) решения для про­дольного или бокового движения, соответствующего меньшей собственной частоте колебаний (со0), изменятся по сравнению с результатами, получаемыми при исследовании изолированных движений, пропорционально следующим выражениям:

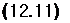ф* 1

фо J /

С00

где фо, со0 -— соответственно амплитуда и собственная частота движения при сох = 0 (т. е. при изолированном движении). В табл. 12.1 приведены результаты приближенных оценок ошибок в амплитуде и частоте колебаний, которые могут иметь место при анализе движений летательного аппарата с кренением, в зависи­мости от соотношения величин угловой скорости крена и меньшей критической скорости крена при рассматриваемом маневре.

В табл. 12.1 в качестве min (со0) следует рассматривать мень­шую из величин соа или со^. При определении меньшей из вели­чин соа и g)£ необходимо рассматривать следующие выражения. Для продольного движения соа следует оценивать по формуле

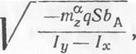(12.12)

Приближенные оценки ошибок в амплитуде и частоте колебаний Таблица 12.1 Ошибки Величина соотношения “ос min (“о) 0.3 0,45 0,55 0,71 Максимальная ошибка по частоте Максимальная ошибка по амплитуде ю % 10 % 20 °о 25 °о 30 °0 45 % N С О о о О О LO О

либо, в случае нелинейной зависимости продольного момента от угла атаки тг (а), по фЬрмуле (18.25), которая может быть за­писана в виде

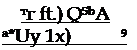
(12.13)

где угол атаки а* определяется из алгебраического уравнения (18.19).

Для Гокового движения в качестве со^ следует брать меньшую из величин:

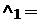
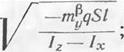
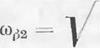(12.14)

(12.15)

ГЛАВА 4