ОБЩИЕ ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ СИСТЕМ

Во втором и третьем параграфе данной главы показано, что Движение самолета в неспокойном воздухе во многих случаях описывается системой линейных дифференциальных уравнений С постоянными коэффициентами. Для любой координаты возмущен* з*

L + ai-^ + .. dtn 1 dtn-* 1

ного движения самолета система линейных уравнений всегда может быть сведена к одному уравнению вида

где x — возмущающее воздействие, известная функция вре­мени;

у — координата движения самолета (реакция на возму­щение), искомая функция;

йі, Ьі — постоянные коэффициенты, зависящие от парамет­ров самолета.

Заметим что для реальных систем всегда справедливо соот­ношение ri^m.

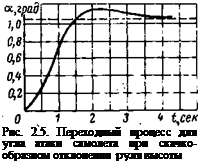Динамические свойства любой системы, описываемой уравне­нием вида (2.31), очень нагляд­но характеризуются переход­ной функции H(t), которая представляет собой реакцию системы или выходную величи­ну при воздействии на систему возмущения в виде единичном функции (единичного скачка). При этом не важно, может лм быть создано в реальных усло­виях возмущающее воздейст­вие в виде единичной функции. Если известно аналитическое выражение для переходной функции, то реакция системы на возмущение практически любой формы может быть найдена с помощью интеграла Дюамеля (интеграла свертки).

В качестве примера на рис. 2.5 изображена реакция самолета по углу атаки при скачкообразном изменении положения руля высоты.

• Если возмущающее воздействие описывается импульсной или б-функцией, то реакция системы называется импульсной переход­ной (весовой) функцией К (()■ Переходная и импульсная пере­ходные функции связаны между собой соотношением

При исследовании динамических систем очень широко исполь­зуется также так называемая передаточная функция. Для полу­чения передадочной функции системы, описываемой уравнением (2.31), введем в рассмотрение оператор дифференцирования

p=d/dt, который преобразует функцию времени в производную этой функции. Производным второго и более высоких порядков соответствуют положительные степени оператора р, т. е. pi=d2ldt2, p3=d3/dt3 и т. д.

Преобразование функции в кратные интегралы осуществляет­ся с помощью отрицательных степеней оператора р, т. е. /7-x=j(. • .)dt, р~2 = jj(…)dt2 и т. д.

Заменяя в уравнении (2.31) производные оператором р в со­ответствующей степени, получим

(аоРп ~Ь а Рп~х ~Ь • • • + an—iP ап) у=

=(ЬоРт + ЬіРт-ї+ ■ • • +bm-ip + bm)x, (2.33)

или

N (р)у=М (р)х. (2.34)

В выражении (2.34) N(p) и М(р) являются рациональными функциями оператора р, т. е. также операторами, но более слож­ными.

Из (2.34) получаем

У=-щ%-х=ЧГуі*(Р)х — (2.35)

Оператор Wylx(p), который, как это вытекает из (2.35), пре­образует возмущающее воздействие в реакцию данной системы, называется передаточной функцией этой системы.

Из (2.35) можно получить и другое часто встречающееся вы­ражение для передаточной функции

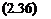Wylx(p)=^.

Для систем, описываемых уравнением вида (2.31), передаточ­ная функция есть дробно-рациональная функция оператора р:

Ь0рт + Ьх рт~1 4- … 4- Ьт-1 р + Ьт

<h ра + Л|рл—1 + … + а„_і р + ап

Рассмотрим некоторые свойства передаточной функции для случая, когда возмущающее воздействие является единичной функцией.

Значение выходной величины в установившемся режиме (/=оо) при воздействии вида единичной функции можно полу­чить непосредственно из уравнения (2.31), если положить рав­ными нулю все входящие в него производные: У=Ьт1ап. Это же значение может быть получено из выражений для передаточной функции (2.35) и (2:37), если положить р=0. Таким образом,

my{t)=mWy:x{p). (2.38

t-*0O р-*- О

Можно также показать, хотя и более сложным путем, что начальное значение выходной величины (t — 0) при воздействии

вида единичной функции определяется значением передаточной функции при р=ОО, т. е.

limy(/)=lim^y/,(/>). (2.39)

t ->0 р-+ ОО

Рассмотрим также используемое ниже понятие частотной ха­рактеристики системы, описываемой дифференциальным уравне­нием (2.31).

Пусть возмущающее воздействие x(t) изменяется по синусоидальному закону, т. е.

л(/)=Лж81п(ш<+и (2.40)

где ф* — начальная фаза возмущаю­щего воздействия.

В этом случае выходная величи­на или реакция системы в устано­вившемся режиме также будет яв­ляться синусоидальной функцией времени:

y(/)=i4ysin(a>*-Hy), (2.41)

где фу — начальная фаза выходной величины.

Представляя синусоидальные величины (2.40) и (2.41) в комп­лексной форме, получаем

х (/«*)=(2.42)

где Лх=Ахе^х — комплексная амплитуда возмущающего воз­действия;

у (/W)=АуеНш‘+V = Луеы, (2.43)

где Лу=Ау^у—комплексная амплитуда выходной величины.

Частотной или амплитудно-фазовой характеристикой системы или комплексной передаточной функцией называется отношение комплексных амплитуд выходной величины и возмущающего воз­действия.

Ь0 (/о>Г + Ьх (У<д)ст * + …+ *т—і У» + b, п й0 ( /<■>)" 4- Ді ( У®)"-1 + • •. + ап-1 У<° + ап

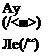Подставляя значения x(jatt) и y(jfat) в уравнение (2.31), на­ходим частотную характеристику системы

Сравнивая (2.44) и (2.37), устанавливаем, что частотная ха­рактеристика может быть получена из передаточной функции путем замены оператора р на оператор /’©. Следовательно,

‘117,„(/»)= 4^-= 4і Л"**’ =»V (“)«*. (2.45)

где Wyix(}»)=Ay! Ах—модуль или амплитудная характеристи­ка;

(p=argU^j,/^(yo>)—аргумент или фазовая характеристика.

Амплитудная характеристика выражает зависимость ампли­туды выходной величины от частоты возмущающего воздействия. Аналогичную зависимость для фазы выходной величины дает фа­зовая характеристика.

В качестве примера на рис. 2.6 приведены амплитудная и фазовая характеристики для угла атаки при синусоидальном дви­жении руля высоты.