ДИНАМИКА ВРАЩАЮЩЕГОСЯ САМОЛЕТА ПРИ ДЕЙСТВИИ НА НЕГО УПРАВЛЯЮЩИХ МОМЕНТОВ

Практически во всех случаях полета самолет сбаланси­рован на отличном от нуля угле атаки, т. е. на пего кроме момента крена действует продольный момент, а иногда и момент рыскания. Наличие несимметрии у самолета в виде момента т0 делает уравне­ния движения неоднородными в связи с чем дополнительно необ­ходимо рассматривать частное решение, которое при т{) — const записывается в виде

Действительная часть выражения (14.1) дает частное решение для угла атаки, представляющее собой установившееся движение, если решение устойчиво, а мнимая часть — решение для угла скольжения. Получить соответствующие решения для аи(3 можно, если умножить числитель и знаменатель выражения (14.1) на комплексно-сопряженное знаменателю выражение. После выде-

113

ления действительной и мнимой частей, получим формулы для установившихся (статических) решений:

mz0 тФ — [AQ — — — my0[xQ ~

(—В«г«р — (iMQ2 — У + f-i-Q2 (Л-J— гпы у2

Отуо (— тф — цЛй — — ~-Щ~) + ~Y “ т<")

(-Р*Ф — рМQ* — ^-)2 + p2Q2 (Л ^ — ти)2

Выражения (14.2), (14.3) явтяются частным случаем соотношений, приведенных в табл. 9.1, которые были получены для общего вида характеристик самолета.

Рассмотрим изменение угловых скоростей сост самолета при приложении управляющего момента. Величина установившейся угловой скорости связана с решением для <р соотношением

РСОст :— ^~9““ f ч ст>

(14.5)

(14.6)

<>у ст — —— Re А, А ‘2^’1г" Ап

 

определим зависимости со2СТ и оо//ст от управляющих моментов:

 

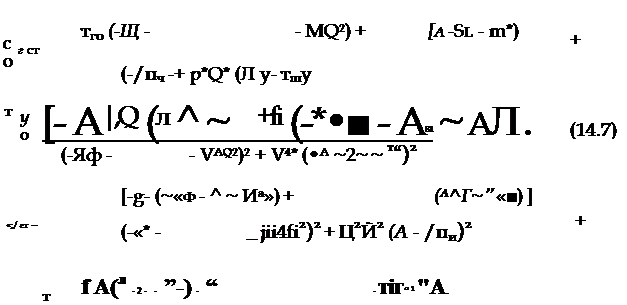(—яї<р — — рЛЙ*)2 + !*^2 (Л ^ — "г«У

Из соотношений (14.2), (14.3), (14.7), (14.8) следует, что:

1) наличие любого из управляющих моментов thz0 либо тт приводит к изменению одновременно как а, так и Р;

2) при приближении величины Q к критическому значению реакция самолета на воздействие управляющего момента сущест­венно возрастает и при отсутствии демпфирования аст и рст стремятся к бесконечно большим значениям;

3) воздействие моментов т20 (ту0) на параметры движения а (Р) при Q > йф изменяет знак на обратный по сравнению с пло­ским движением при Q ~ 0, а знак перекрестного воздействия mzi) (туо) на р (а) от величины Q не зависит и постоянен;

4) реакция самолета по угловой скорости 6)ZCT (со^ст) при приложении управляющего момента mzQ (ту0) сохраняет неизмен­ный знак при всех величинах Q. При этом, перекрестная реакция со* == / (tfiyo) и со у = f2 (m20) при увеличении £2 > Пф изменяет знак на обратный.

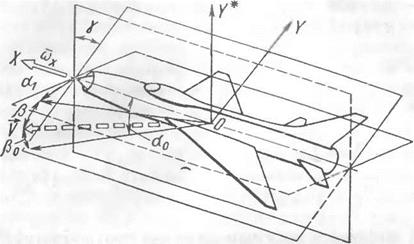
Для более наглядного объяснения полученных свойств целесо­образно рассмотреть движение самолета, взяв в качестве системы осей координат оси 0X*F*Z*, которые колеблются вместе с само­летом по ос и р, но не вращаются по крену. Соотношение между системами осей координат видно из рис. 14.1. Невращающаяся система координат удобна тем, что позволяет проследить траекто­рию движения носика фюзеляжа самолета вокруг вектора скорости.

Для вывода уравнений движения самолета в осях OX*F*Z* можно воспользоваться уравнением (13.7) и преобразованием

ф-= фе~‘^1т, (14.9)

которое ставит в соответствие угол ф во вращающейся системе координат углу ф в невращающейся системе. Подставляя в урав­нение (13.7) соотношение (14.9), получим уравнение для ф:

Ф" + [-£- — /П» + фШх] ф’ +

Угол ф представляет собой пространственный угол атаки фюзеляжа самолета относительно невращающейся системы осей координат. При записи уравнений движения относительно такой системы координат в правых частях уравнений движения появ­лялся периодически меняющийся член, величина которого про­порциональна /н. г. Наличие такого возмущающего члена в правой части делает уравнения неоднородными и приводит к появлению в решении члена Л3е~ *QpT. При наличии периодического возму­щения в случае, если характеристическое уравнение системы имеет колебательные корни, можно ожидать резонансные явления. Реше­ние для ф наиболее просто получить, произведя замену перемен­ных (14.9) в решении (13.8) для угла ф:

ф = т + Л2е(^-1’ЭД * ~ Л3е-Шит. (14.11)

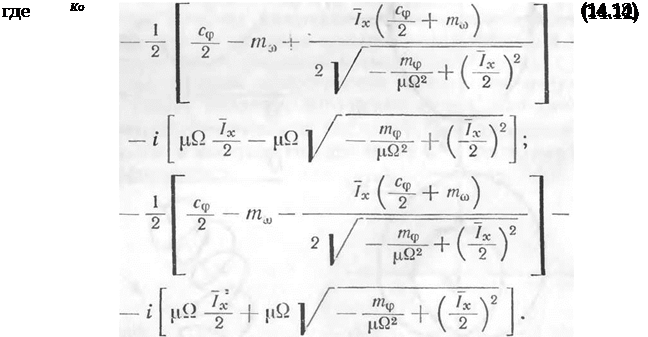Вводя новые обозначения для корней характеристического урав­нения, получим

Для получения более наглядных приближенных оценок зави­симости корней от Q рассмотрим самолет, у которого Iх /, так,

что можно приближенно принять Iх 0. Выражения для корней

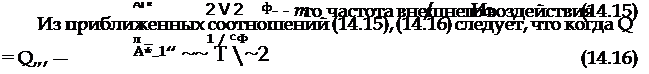в этом случае существенно упростятся:

совпадает с частотой собственных колебаний. В этом случае в системе имеет место резонанс, и амплитуда колебаний увеличи­вается, достигая значений, определяемых величиной демпфирова­ния самолета. При увеличении частоты возмущения до величины, превышающей резонансную, реакция самолета по углу атаки и

скольжения отстает по фазе от возмущения на 180 , что соответ­ствует изменению знака вынужденной составляющей решения. Это выражается в обращении знака связи между а и mz0 (р и ту0) при вращении самолета cfi > £Зф. Аналогично обстоит дело и в общем

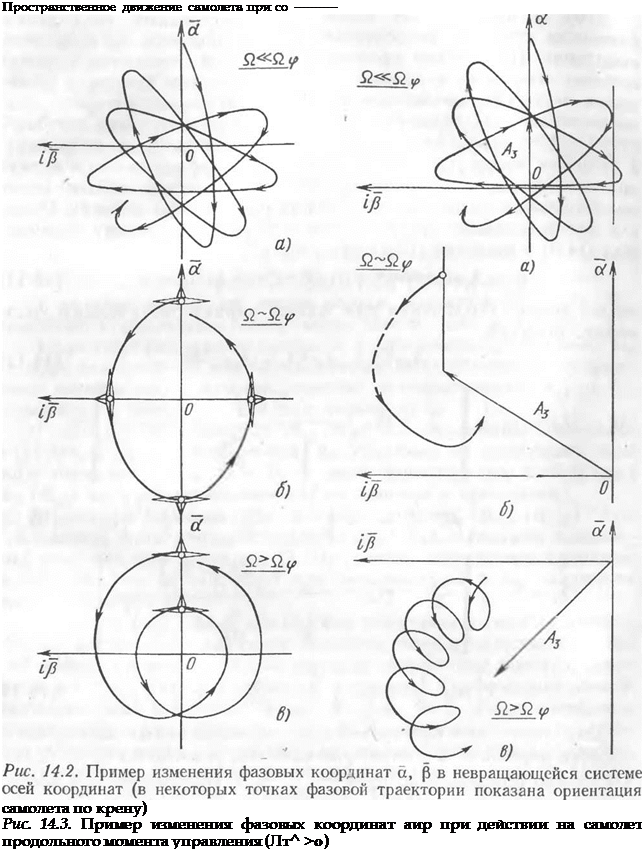
случае, когда /Л Ф 0. Используя представление решения для ф в виде (14.12), можно рассматривать изменение параметров движе­ния на фазовой плоскости для переменных а, р (ф = а + *Р). На рис. 14.2 представлены примеры изменений параметров движе­ния для случая Q < £>ф (я), Q ~ Пф (б) и Q > йф (в). На этих рисунках показана также ориентация самолета по крену в различ­ных фазах движения.

Аналогично могут быть получены фазовые траектории для параметров движения, определяемых в связанных с самолетом осях координат, т. е. для обычных углов атаки и скольжения. Для этого необходимо воспользоваться представлением решения в виде

(13.8) и учесть выражение (14.9) для определения Ая. Примеры фазовых траекторий для управления т21) приведены на рис. 14.3 для значений Q < Пф, Q ~ Qfp и Q > Пф.

Полученные свойства движения самолета при продольном и путевом управлении в процессе вращения сохраняются и в общем случае, который будет рассматриваться в последующих главах. Наиболее существенным ограничением применения результатов, полученных ранее, является допущение о том, что самолет не

имеет поперечной устойчивости (ГПх = 0). Это допущение позво­лило считать, что в возмущенном движении Q = const, что в общем случае не выполняется.