ПРЕОБРАЗОВАНИЕ УРАВНЕНИЙ И АНАЛИЗ УСТОЙЧИВОСТИ ДВИЖЕНИЯ

При сделанных ранее допущениях о симметричных характеристиках самолета по углу атаки и скольжения в случае,

когда момент поперечной устойчивости nix равен пулю, целый ряд задач может быть исследован значительно более полно, чем это было возможно в общем случае.

Рассмотрим устойчивость и особенности движения самолета при установившемся вращении относительно продольной оси с со, = Q — const, характеристики которого удовлетворяют сформулированным ранее условиям. В этом случае уравнения движения в безразмерном виде, записанные относительно главных осей инерции, имеют вид

(0; + А[)мхЫу — т%а + т&<йг + тг0;

Преобразование уравнений для анализа устойчивости 107

со у — В\ыхы2 = га[$ + тууійу + туо

СО* = ГПхХW + т*0 • (13.2)

Произведем преобразование уравнений (13.1) и (13.2) к виду, удобному для исследований. В силу принятой нами аэродинамиче­ской и инерционной симметрии самолета можно ввести следующие обозначения:

Су = Сг = Ctlz(j : — til у = /Нф,

/и®* — т®» = т0,; Л-В — 1 —7,,

где /* = /.//; 1 = 1У = /2.

Входящие в правые части уравнений (13.1) и (13.2) слагае­мые тА0, т^о и т20 представляют собой моменты управления.

Из уравнений (13.1) и (13.2) видно, что в рассматриваемом слу­чае при тх0 = const угловая скорость крена соА. постоянна по величине. Отсюда, в частности, следует, что уравнения (13.1) можно рассматривать отдельно от уравнения (13.2) и считать, что о) = Q = const. Симметричный вид уравнений движения (13.1) позволяет несколько упростить их запись благодаря переходу к комплексным переменным — углу атаки и угловой скорости с помощью соотношений

ср = а + ф;

ю = 0>г + (Гда 1 — V — 1 )•

Произведя преобразования, получим

ф’ — м“ — ф;

со’ — iAlQСО = /ПфГр -{- /77^СО /770,

где /770 = /7720 + Іту0.

Систему уравнений (13.4) удобно привести к одному уравнению, описывающему изменение комплексного угла атаки самолета ср. Из первого уравнения системы (13.4) получим

= у [ф* + ф’];	(13.5)
	(13.6)

Подставляя выражения (13.5) и (13.6) во второе уравнение системы

(13.4) и группируя члены при соответствующих производных угла Ф, получим

ф" + [-J- — т<* — *MQ (! + А)] ф’ +

+ [-fun* — цМО» — — 1|«о ( л — /пл)] ф = тоМ. (13.7)

Уравнение (13.7) является линейным неоднородным уравне­нием с постоянными комплексными коэффициентами. Для его ре­шения можно использовать методы, аналогичные методам решений линейных уравнений с действительными коэффициентами. Решение уравнения (13.7) может быть записано в виде

Ф= і41еЛ‘т + і42є**х+ А3у (13.8)

где коэффициенты Аъ /1-2, А3 являются комплексными постоян­ными, зависящими от начальных условий. Первые два члена выражения (13.8) описывают общее решение однородного уравне­ния (13.7), а коэффициент А:$ —частное решение неоднородного уравнения

А,=—————— ————— ^—————————— г-. (13.9)

—fW”tp——— ~ V2AQ2 — гцQ — Л m^j

Корни и Х.2 определяются из выражения

^1, 2 =Y ————- т:о (1 “Г ^)j zb

zb — у f ГП. Л i[iQ (1 + A)J —

— 4 [~ртф — — р2/Ш2 — ipQ (л — т,0)] . (13.10)

Из выражения (13.10) видно, что корни?4j2 в общем случае являются различными комплексными корнями и решение (12.8) состоит из колебаний двух различных частот. С учетом того, что квадратный корень в выражении (13.10) представляет собой комплексное число, выражения для корней характеристического уравнения можно переписать в виде

71,2 — —(Rex ± Re.) + і (Im! A Im2), (13.11)

где —Rex, Іш! и —Re2, їгп>—действительные и мнимые части соответственно первого и второго слагаемых в соотношении (13.10).

Преобразование уравнений для анализа устойчивости

Для устойчивости движения необходимо выполнение условий

Re, > 0, (13.12)

Rei>|Re2|. (13.13)

Остановимся на анализе этих неравенств. Учитывая, что

Rei = т (-у — — т°)’ ИЗ. 14)

получим, что условие (13.12) всегда выполняется для аэродинами­чески устойчивого летательного аппарата, поэтому необходимо анализировать только условие (13.13). Считая демпфирование малым, на основании соотношения (13.13) выведем приближенное условие устойчивости. В подкоренном выражении формулы (13.10) в случае малого демпфирования коэффициент при мнимой части существенно меньше по величине, чем действительная часть, поэтому при извлечении корня можно сохранить только первые два члена его разложения в ряд Тейлора. Выполняя эту операцию, получим приближенное выражение для корней и а2:

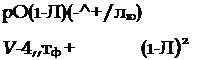+ /| —4ртф + p2Q2 (1 — Л)2 ’.

(13.15)

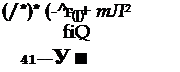Используя выражение (13.15), условие устойчивости (13.13) можно представить в виде

Неравенство (13.16) получено в предположении, что выражение под радикалом в формуле (13.15) положительно. Иными словами, дополнительно предполагается, что выполняется неравенство

m, t < A ^ Clxf. (13.17)

Неравенство (13.17) является приближенным условием апериоди­ческой устойчивости движения вращающегося самолета. Это нера­венство всегда выполняется для статически устойчивого самолета и фактически является условием допустимой неустойчивости, кото­рая может быть скомпенсирована гипроскопической устойчивостью при вращении. Из сравнения условий (13.16) и (13.17) видно, что условие устойчивости (13.16) является более сильным и его выпол­нение заведомо влечет за собой выполнение условия (13.17).

Действительно, условие (13.16) можно переписать в следующем виде:

тф<^н^г(А)2К. (13.18)

Величина /С, как это следует из выражения (13.19), положи­тельна и лежит в диапазоне между нулем и единицей:

1^/С^О. (13.20)

Когда К = 1, получаем приближенные условия апериодической устойчивости (13.17), с другой стороны, если К = 0, то динами­чески устойчивым может быть только статически устойчивый само­лет. На практике величина К отлична от нуля и единицы и при­нимает некоторые средние значения.

Рассмотрим зависимость корней (13.15) от величины угловой скорости вращения самолета по крену. Из выражения (13.15) следует, что при вариации величины Q основному изменению под­вержены мнимые части корней. Это особенно наглядно видно, если рассматривать предельный случай инерционных характеристик самолета, когда для моментов инерции выполняется условие 1Х « /, т. е. /1 ^ 1,0. При этом условии выражения для корней дополнительно упрощаются и приводятся к виду

” 2 ~ т&)) ~ j *» (13.21)

= — тЛ) + т(о-|/ —22-). (13.22)

При изменении величины Q происходит изменение мнимых частей корней, которые при ії Ф 0 становятся различными. Это свиде­тельствует о существовании в возмущенном движении самолета двухчастотных колебаний. У одной из составляющих решения частота возрастает по мере увеличения Q, а у второй сначала

убывает по модулю, обращаясь в нуль при Пф =

(рис. 13.1), а затем изменяет знак и начинает возрастать.

приближенно равна собственной частоте колебаний, а более точно совпадает с определением критической скорости крена, введенной в гл. 2. Путем анализа общего вида решения для <р при т0 — 0 можно представить вид фазовых траекторий иа пло­скости координата, ф. Движение происходит относительно особой точки в начале системы осей координат. Поскольку характеристи­ческое уравнение имеет две пары комплексных корней с отрица-

Преобразование уравнений дли анализа устойчивости

тельной действительной частью, то особая точка является устой­чивым фокусом. Следует отметить, что фазовые траектории имеют пространственный характер и зависят от четырех фазовых пере­менных. При их изображении в виде проекции на плоскость (а, Р) получим картину, при которой фазовые траектории могут пере­секаться, так как остальные фазовые переменные (со^, coz) на этих иллюстрациях не изображены.

В решении (13.8) коэффициенты А1 и Л.2 являются постоянными комплексными числами, зависящими от начальных условий, которые на фазовой плоскости а, ф могут быть представлены

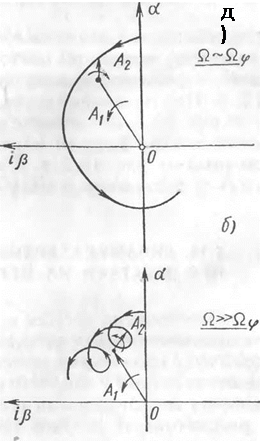
в виде векторов. При изменении аргумента т эти векторы, из-за наличия множителей вида ехр (пуг) (где т) = Im ХЬ2), начнут пово­рачиваться, причем, если і] > 0, то вращение происходит от поло­жительного направления действительной оси к положительному направлению мнимой оси, а если ц < 0, то к отрицательному на­правлению мнимой оси. При этом векторы Aj ехр (^т), Ло ехр (А2т) благодаря множителю е^т, будут дополнительно изменяться по модулю. Эти качественные соображения позволяют представить вид фазовой траектории движения на плоскости (а, ф). На рис. 13.2, а приведены соответствующие примеры изменения фазовых координата, р при вращении самолета с малой величиной Q £2ф. Для этого случая мнимые части корней имеют разные знаки и векторы А і ехр (^Тт) и А 2 ехр (^2т) вращаются в разные сто­роны.

При приближении величины Q к критическому значению Q = = Йф скорость вращения вектора А2 уменьшается (стремится к нулевой) и фазовая картина принимает вид, изображенный на рис. 13.2, б. При дальнейшем увеличении Q так, что Q > Пф, как следует из рис. 13.1, обе мнимые части комплексных корней имеют одинаковые знаки, фазовая картина меняется и принимает вид, изображенный на рис. 13.2, в. В этом случае векторы Аг ехр (Ajt) и А2 ехр (А2т) вращаются в одну сторону.