ПРИБЛИЖЕННЫЕ НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ПРИ со* < юр < соа И АНАЛИЗ ИХ СВОЙСТВ В СЛУЧАЕ МАЛОГО ДЕМПФИРОВАНИЯ

Будем рассматривать пространственное движение само­лета для тех случаев, когда | cov | coa и критические скорости крена существенно различны, причем

C0fl<CDa. (15.1)

При выполнении приведенных условий можно приближенно счи­тать, что угол атаки самолета в возмущенном боковом движении не изменяется, а ~ а’ ~ 0. В этом случае из уравнения для а’ получим приближенное соотношение для определения угловой скорости о)г, вызванной боковым движением самолета:

to2 = Pav (15.2)

Подставив это соотношение в уравнения пространственного движе­ния (3.13), получим систему нелинейных уравнений, приближенно описывающих боковое движение самолета:

Р/ Р0^ — f — pto^oco -|—2~ р;

соу = ту р + tnyl<)y + бросцР + А ту

СО* — Шхр -{- ГПхХ®х + A/77jc.

119

Таким образом, уравнения пространственного движения самолета разделяются на две группы уравнений, отличающиеся темпом изменения параметров: на систему уравнений (15.3), описывающих медленно меняющиеся параметры, и уравнения, описывающие квазиустановившиеся движени я:

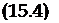со2 = (5сог, ос = ос0,

выполняющиеся для параметров движения, при быстром затухании возмущений. Как отмечалось в § 12, такое разделение уравнений возможно при условии, что решения для быстрых переменных являются устойчивыми при любых значениях медленно изменяю­щихся переменных, т. е. величин р, G)*, (by. Это требование при сформулированных в начале параграфа ограничениях на величину со* для уравнений продольного движения выполняется. Более того, в рассматриваемом случае могут быть сделаны некоторые оценки точности выполнения соотношений (15.4).

Оценим величину отношения критических скоростей крена для движений тангажа и рыскания соа сор, при которых равенство (15.2) выполняется с достаточной для практических целей точностью. Рассмотрим сначала, при каких соотношениях между о)а и сор выполняется соотношение (15.2) в установившихся режимах дви­жения. Воспользовавшись формулами для статических решений (табл. 9.1) и считая демпфирование малым (£ ^ 0), получим

4

оуІ 2 т^у а у

~2

2 trfiy

а у

Если потребовать приближенного выполнения соотношения (15.2) для всех значений о>* из диапазона 0 < | со* | < сор, то получим условие

С0£	Вс
= е«1
(15.6)

 

(Для выполнения соотношения (15.2) с ошибкой не более 10 % необходимо принять, ЧТО 8 =0,1.)

Рассмотрим второе условие, при котором выделялись уравнения бокового движения, а именно неизменность угла атаки (Да ~ 0). Из формулы для статических решений (табл. 9.1) следует:

До^ст

а0

1

 

www. vokb-la. spb. ru — Самолёт своими руками?!
Демпфировании
<g; toa ирії малом	121
120
Пространственное движение
щениях. При сор соа < 0,3 движение близко к изолированному боковому, которое реализуется в случае, когда сор соа -> 0. Рас­четы по формулам (15.6) и (15.7) показывают, что соотношение (о f(ba ^ 0,3 можно считать условием практической применимости приближенных уравнений бокового движения (15.3). Приступим к анализу свойств полученной системы нелинейных уравнений (15.3), описывающих боковое движение самолета. Из сравнения уравнений (15.3) с обычными линейными уравнениями бокового движения следует, что в уравнениях (15.3) опущены гра­витационные члены, и, следовательно, они неточно описывают медленные движения типа спирального, однако учтены инерцион­ные моменты, что позволяет с их помощью исследовать управляе­мые движения, сопровождающиеся большими угловыми скоро­стями крена. Изучение качественных свойств нелинейного бокового движе­ния самолета начнем с модельного случая, когда предполагается, что самолет не обладает демпфированием. Уравнения движения в этом случае преобразуются к виду Р’ -•= мо</ + и«о«л-; сну — + £|Шд Р; (15.9) — Р- Приравнивая производные нулю, получим выражения для коор­динат особых точек: Р —0; (Dy = 0; о).= 0. (15.10) Кроме этой особой точки, которая сохраняется и при наличии демпфирования, имеется особая прямая, которая сплошь состоит из особых точек и существует только при отсутствии демпфиро­вания: > (3 = 0; со,,——а0соА. (15.11) Система уравнений (15.9) может быть проинтегрирована, что позволяет найти решения для фазовых траекторий в конечном виде. Из второго и третьего уравнений системы (15.9), получаем Уравнение
Чтобы величина Да ^ Даст не превосходила значение Да ^ ~ 0,laj, необходимо выполнение условия ^ о,3. <*>сс Качественный характер влияния величины сэр соа на боковое движение самолета виден из рис. 15.1, на котором приведены ре­зультаты моделирования движения самолета при больших возму­
toy
d(0y Гпх + В^х с! ых т& из которого после интегрирования следует:
(15.12)
=0,6
Вх
—з Ых,
Рис. 15.1. Примеры движения на фазовых плоскостях Р, (o;v и сод — для раз­личных соотношений величин критических скоростей крена по рысканию сор И тангажу
(15.13)
Ыу + Сі =—	tox—

ҐТространственное движение самолета при

где С,—произвольная постоянная, значение которой определяется начальными условиями для переменных (0) и (0). В частном случае нулевых начальных условий соЛ (0) = (0) = 0 постоян­

ная Сг = 0.

выражение (15.13) представляет из себя уравнение цилиндри­ческой поверхности с образующей, параллельной оси 0(5. Отметим, что из выражения (15.13), следует, что Сг может принимать любые как положительные, так и отрицательные значения в зави­симости от начальных условий.

Поделив уравнение для (5′ на последнее уравнение системы

(15.9) , с учетом выражения (15.13) получим уравнение для фазовых траекторий

d р d(ox

(15.14)

Проинтегрировав (15.14), получим уравнение фазовых траекторий в явном виде:

 

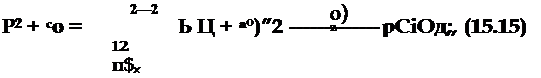где С0 — вторая произвольная постоянная, определяемая началь­ными условиями для Р (0) И со* (0).

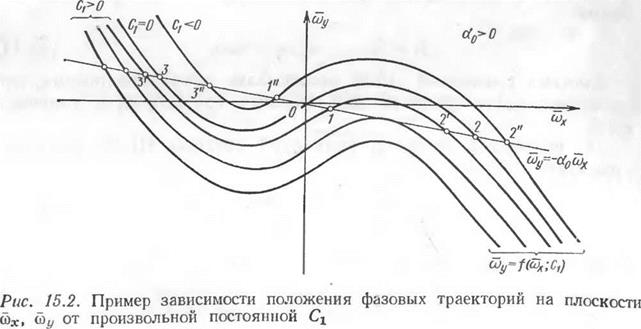
Рассматриваемая нами система уравнений (15.9) не является грубой, что привело к появлению бесконечного числа особых точек, определяемых прямой (15.11). Если какая-либо фазовая траекто­рия пересечет прямую (15.11), то соответствующая точка пересече­ния является особой точкой для рассматриваемого движения (рис. 15.2). Отсюда следует, что каждой комбинации начальных

Рис. 15.3. График зависимости pCi (со*), используемый для определения зна­чений со* в особых точках

 

условий по переменным со* и <ЬУ соответствуют свои особые точки на прямой (15.11).

Координаты особых точек могут быть получены из одновремен­ного решения уравнений (15.11) и (15.13), которые приводятся к одному нелинейному уравнению для определения значений координаты со*:

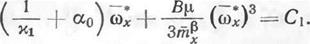(15.16)

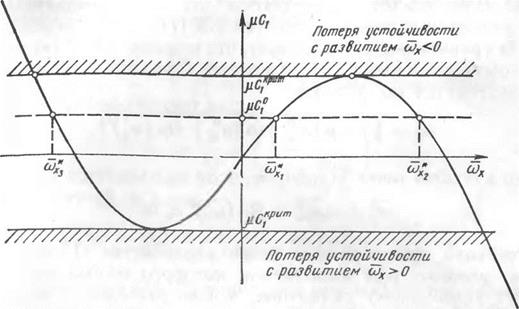
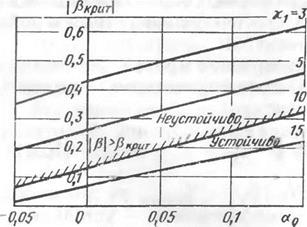
Величины со£ удобно находить графически, строя зависимости от со* левой части равенства (15.16) (рис. 15.3). Значения остальных координат в особой точке определяются из соотношений

Рассмотрим устойчивость движения в окрестности особых точек, определяемых величиной й*х. Уравнения (15.9) в вариациях относительно параметров движения в особой точке будут иметь вид:

Р’ = рсоу + ра0со*;

со ‘у = [ml + В1 (со;)2] Р;

‘ Ро со* = т р.

Продифференцировав первое уравнение по т и подставив выраже­ния ДЛЯ Ыу и coi из второго и третьего уравнений, получим

Из уравнения (15.18) определяются два корня характеристиче­ского уравнения системы уравнений (15.17), третий корень равен нулю. Из уравнения (15.18) следует, что решение для (3 (т) в окрест­ности особой точки имеет колебательный характер. Частота колеба­ний определяется по формуле

0)0 = ~j/~-—Р (/л!) “Ь &оМх “Ь — Вр (со*) ). (15.19)

Решение в особой точке устойчиво, если выполняется неравенство

ту + йот* + Bf. i (о>х)2< 0, (15.20)

и неустойчиво при обратном знаке неравенства (15.20). Таким образом, условие, при выполнении которого особая точка соот­ветствует устойчивому движению, можно записать в виде

|-;|<|/ЕВрЛ = -кг+^ (15.21)

Из рис. 15.2 и 15.3 следует, что при некоторой величине Сг — Cf, т. е. при некоторых начальных условиях, одна из неустойчивых особых точек (Аг° 2 или 3) сливается с устойчивой особой точкой (№ 1). Это произойдет при значении постоянной Cf, определяемой по формуле

СГ = ^-(1+а0х,)3/2-^-. (15.22)

Такое значение Cf соответствует величине угловой скорости в особой точке:

СО* крит — C’)f3 / 1 "І — •

Учитывая выведенные ранее условия устойчивости и неустойчи­вости решений в особых точках (15.21), получим, что все особые ТОЧКИ, ДЛЯ которых угловая скорость меньше Ш* крит ЯВЛЯЮТСЯ

устойчивыми, а для которых | со* | > со*кр1ТТ соответствуют седло­вым особым точкам.

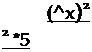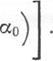Следует отметить, что через особую точку пройдет фазовая траектория, удовлетворяющая вполне определенным начальным условиям, которым соответствует некоторое значение постоянной С0. Это значение С0 находится из условия прохождения фазовой траектории, описываемой уравнением (15.15), через особую точку с координатами |3 = 0; (Ьх = со*. Отсюда получаем

125

Рассмотрим частный случай начальных условий, соответствующих воздействию на самолет порыва ветра:

Р(0) = Р«; ю,(0) = (0) = 0. (15.25)

В этом случае Сг = 0 и уравнение фазовых траекторий на пло­скости (<1>/у, со*) приобретает вид

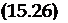— 1 — ( (х>1

а на плоскости (В, со,) вид

Из соотношения (15.27) видно, что при достаточно малых угло­вых скоростях крена, когда можно опустить член с со*, фазовыми траекториями будут либо эллипсы, если выполняется условие

rrfij -f ct0m* <0, (15.28)

либо при невыполнении этого условия — гиперболы. В последнем случае движение неустойчиво. Критерий устойчивости (15.28) совпадает с обычным приближенным условием устойчивости для линейных уравнений бокового движения [13].

Для рассматриваемого случая имеются три особые точки с координатами:

	1) р = 0, 2)13 = 0,	3) р = о,
	— —* со* = со*>	* <0* = —со*,
	со* = и>у = 0, со у = —а0со*х,	* (0у :=: (Х, ф)х*	(15.29)
где	®:==cop/ З(1+Кіа0)-		(15.30)

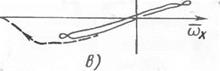
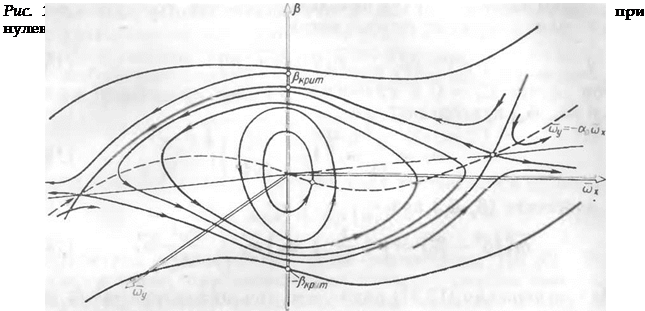
Можно показать, что особые точки 2 и 3 являются седловыми особыми точками и через них проходят сепаратрисные кривые, разделяющие области устойчивого движения в окрестности особой точки У, от области неустойчивого движения, сопровождающегося неограниченным возрастанием <ЬХ. Характер фазовых траекторий системы уравнений (15.9) виден из рис. 15.4.

Для нахождения уравнения сепаратрисной кривой, определим величину ро = Ркрит» ПРИ которой фазовая траектория проходит через точку р = 0, со* = со*. Получим:

о ____ 1 + Ка0 “I f 3

Ркрит Kl у 2В ‘

Если при ступенчатом порыве ветра | ро | < Ркрит» то движение самолета ограничено (при наличии демпфирования —устойчиво).

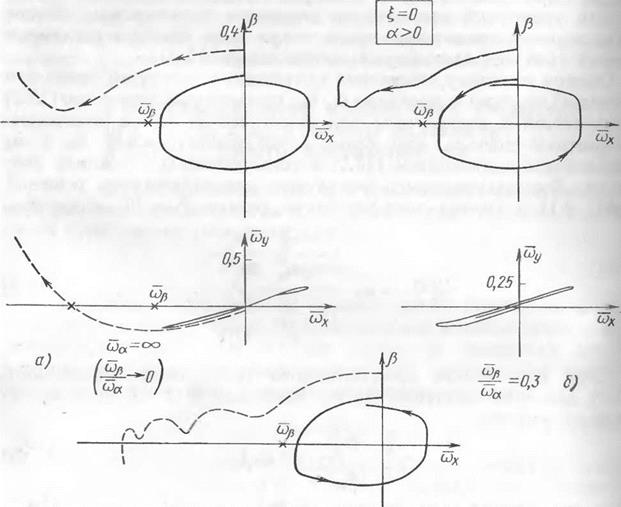
При | ри | > ркрит движение апериодически неустойчиво. Таким образом, при анализе устойчивости возмущенного движения само­лета в дополнение к условию (15.28) необходимо учитывать условие рI < Рк] ит* На рис. 15.5 приведены примеры зависимости Ркрит от величин щ и а0 Характер движения самолета при поры­вах ветра, полученный путем моделирования на АВМ при х0 > О, виден из рис. 15.6, а, Моделирование проводилось с использова­нием практически точных уравнений движения. Фазовые траекто­рии на рис. 15.6 соответствуют случаю относитечьно малого демп­фирования. Влияние степени демпфирования на величину критического возмущения может быть оценено с помощью рис. 15.7, на котором построена зависимость ркрит от 1/^ат> где п ат — количество колебаний до практического затуха­ния (п ат 0,48п 5). Эга величина варьировалась измене­нием производных ™-{уУ и в Одинаковое число раз

относительно номинального зна­чения.

Как было получено ранее, в общем случае начальных усло­вий положение особых точек и вид фазовой картины движения определяются постоянной Clt

Рис. 15.5. Пример зависимости от ос0 ве­личины возмущения от ветра | Ркрит |» приводящей к потере устойчивости движения

12?

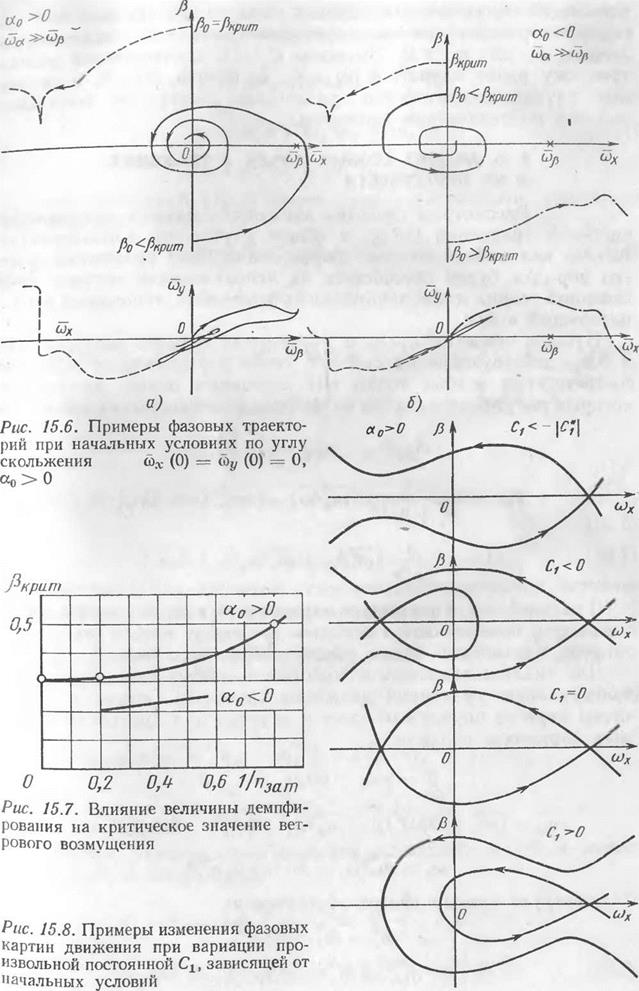
зависящей or начальных условий по cov и cov. На рис. 15.8 по­строены примеры изменения фазовых картин при вариации ве­личины С-, для а0 > 0. Значение С. = 0 соответствует рассмо­тренному ранее случаю (3(0) =ро, соА. (0) = со7 (0) = 0, а осталь­ные случаи соответствуют различным сочетаниям начальных условий по параметрам движения.