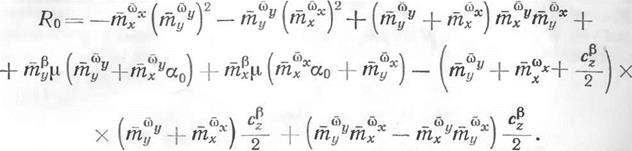АНАЛИЗ ОСОБЫХ ТОЧЕК И ДВИЖЕНИЯ В ИХ ОКРЕСТНОСТИ

Рассмотрим свойства движений самолета, описываемых системой уравнений (15.3), в общем случае его характеристик. Анализ нелинейной системы дифференциальных уравнений треть­его порядка будем основывать на использовании методов каче­ственной теории дифференциальных уравнений, описанной в гл. 3 настоящий книги.

Пусть с помощью органов управления созданы моменты ДтА и Дrhy, действующие на самолет. Этим управляющим моментам соответствуют особые точки или состояния покоя, координаты которых могут быть найдены из системы алгебраических уравнений

4

от ^0““ Г 2ц Рст’

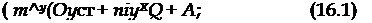
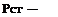т& + jBpQ2

Q =———— і — (m^PcT + тУыу ст + А тЛ.

ГУ! ^

В дальнейшем, в настоящем параграфе, в качестве независимого параметра, описывающего исходное движение, вместо отклонений органов управления будем рассматривать величины Рст и Q.

Для анализа движения в окрестности особых точек произведем линеаризацию уравнений движения самолета. Сохранив только члены первого порядка малости и опуская для краткости записи знак вариации, получим

4

Р’ = + ~2~- Р;

ы’у = {ml + B. iiQ2) р — rtiyV(Oy -f [щх — j — 2Вррст) со*; (16.2)

‘ і ^*7/ і (Зр

со* = тх со* + тхуа>у + т*р.

Сгруппируем члены и введем обозначения:

inI — ml л — Q2;

тУ ■— т’ух -j-2BpQpC[.

www. vokb-Ia. spb. ru — Самолёт своими

иализ особых точек и движения в их окрестности

С учетом этих обозначений уравнения преобразуются к виду, совпадающему с видом линейных уравнений бокового движения:

Р* — [.ІОСдСдх -|- ~2~ pi

(Оу = /72^Р — f — Шу *4 -(- Шу’ (i>xj ‘ І І бо

to* = т/(0Х + іпх уи>у ті Р-

Система уравнений (16.3) имеет характеристическое уравнение 3-го порядка

Ра + В2р2 + BlP + Во = 0, (16.4)

В = tnyunixx — ра 0т% — цпіу — тУіщ/ — f- ~ — j — (16.5)

, _ б л/ b)_. w В ■ — 63#. _ R — m R

0 = —mxwiy — іа0тхупґу — j — тууіа0т’х + mxmvy —

Так как B2 > 0, то условия устойчивости имеют вид:

Во > 0: (16.6)

R = В2ВХ — В0 > 0. (16.7)

Неравенство (15.6) является условием апериодической устойчи­вости и может быть преобразовано к виду

(

Р

rhl-~ тУ) + pBQ2 — /п*»а0) > О,

(16.8)

где

Boo = trixl1 [ту! «о — nhxj + tnlx — 0) —

, — — сг ( — & и — to — _ _ о)„

~2 [іПуУтхх — mxvmy у

Аналогично, условие колебательной устойчивости (16.7) может быть преобразовано к виду

R = Яо + + ^Г"«о + Ц іXів& +

+ 2рВйрст [ [туу + т“х) inxy -1- рт£] >0, (16.9)

5 Бюшгенс Г. С.

где

Рассмотрим влияние угловой скорости Q и угла скольжения рст на устойчивость движения самолета. Члены, определяющие это влияние, выделены в выражениях для В0 и R. Из (16.8) и (16.9) следует, что условия устойчивости представляют собой комбинации членов, получаемых при анализе устойчивости линейных уравне­ний бокового движения и нелинейных добавок. В случае, когда самолет обладает аэродинамическим демпфированием, вращение с угловой скоростью приводит к уменьшению как апериодической, так и колебательной устойчивости движения. Для самолета, обла­дающего аэродинамической поперечной устойчивостью (т* < 0), при движении со скольжением и вращением так, что £2рст > 0, степень устойчивости апериодического движения возрастает, а колебательного уменьшается. При обратном знаке этого произве­дения, а именно, когда £2рст < 0, апериодическая устойчивость убывает, а колебательная повышается. Само по себе начальное скольжение не влияет на устойчиво ть движения самолета, если аэродинамические характеристики не зависят от р, а начинает существенно влиять только при выполнении маневров крена (т. е. когда £2 Ф 0). Влияние угловой скорости крена на устойчивость движения проявляется и при отсутствии угла скольжения само­лета.

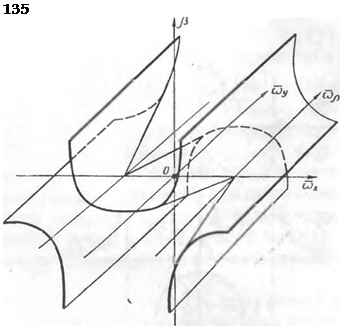
Примеры границ областей устойчивости на плоскости пара­метров (fi/cop), (m^pCT/*їїхХй$) приведены на рис. 16.1.

Как следует из формул (16.8), (16.9), границы областей устой­чивости в координатах рст, Q определяются только аэродинами­ческими характеристиками самолета и величиной угла атаки. В связи с этим они являются универсальными для всех возможных маневров крена. Анализ устойчивости конкретного маневра может быть выполнен, если известны соответствующие величины рст и Q. Следует отметить, что полученные условия устойчивости верны и для угловых скоростей Q > сор, при оговоренном ранее ограниче­нии, ЧТО Q G>ct-

Уравнение (16.4) при Q = Рст =0 является приближенным характеристическим уравнением бокового движения самолета и обычно содержит один действительный отрицательный корень и два комплексно-сопряженных корня с отрицательной действитель-

Анализ особых точек и движения в их окрестности	131

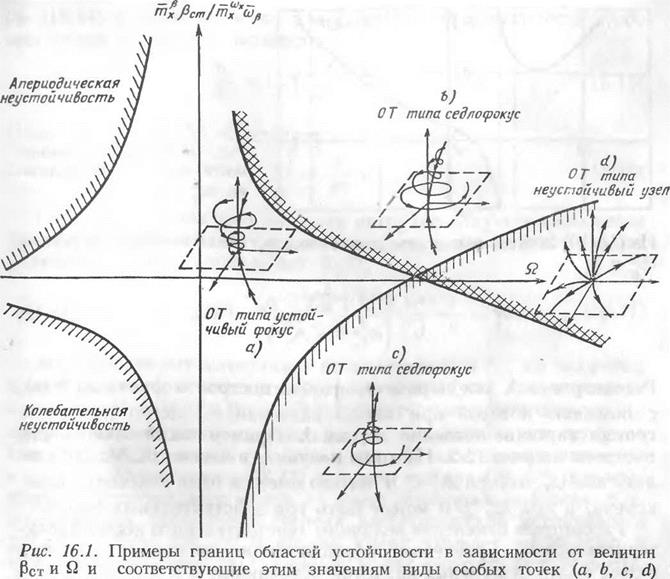
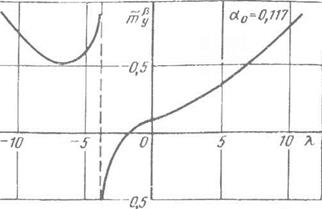
ной частью. Учитывая существенную важность для дальнейшего анализа знания зависимости величины действительного корня от параметров самолета, в первую очередь от значений параметров движения в особой точке, рассмотрим один из наглядных методов нахождения такой зависимости. Рассмотрим зависимость корня К

от величины Щ. Пусть К — корень, удовлетворяющий характери­стическому уравнению (16.4). Тогда, подставив а в (16.4) вместо р, получим тождество

Я3 ~Г В2Я2 + (В[ — u/Лу) Я — j — [в0 + [nixx — а-о1ПхУ) цт£] = 0, (16.10) где

В = thyyn£x — м«о 1Пх — тУпіуХ + ~ (myv + т“*); (16.11)

~ „ / О) _ (Ь Ст ( —

В0 = —mV [тух — а0m/J————- (т/т/ —

Рис. 16.2. Пример зависи­мости корня X от величи­ны

Из (16.10) можно выписать зависимость, связывающую величину

У

(16.12)

Рассмотрим изменение величины действительного корня харак­теристического уравнения, обусловленное движением самолета с отличными от нулевых значений величинами Q и (Зст. Пусть X — корень характеристического уравнения (16.4) при П = (Зст = 0. При появлении в коэффициентах характеристического уравнения дополнительных членов, пропорциональных Q, [5СТ, действитель­ный корень изменится. Для оценки изменения величины действи­тельного корня при вариации некоторого параметра v можно вос­пользоваться следующим приемом. Обозначим выражение для характеристического полинома через F (Я, v), где X — действитель­ный корень характеристического уравнения

(16.13)

Пусть при v 0 характеристическое уравнение (16.13) имеет корень Х0. Тогда F (X0t v) = 0. Поскольку при малом изменении параметра v характеристическое уравнение должно выполняться при некотором значении корня X, можно продифференцировать выражение (16.13) по v и приравнять эту производную нулю:

(16.14)

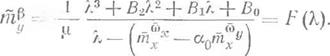
133

Из (16.14) следует формула для определения зависимости dX/dv при малом изменении параметра v:

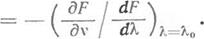(16.15)

Изменение корня АХ определяется по формуле

AX = -^v. (16.16)

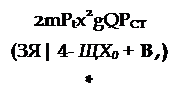С использованием этой методики нетрудно получить выражение для AX, обусловленное влиянием членов в характеристическом уравнении, пропорциональных |3CTQ:

Из приведенных материалов по влиянию Q и (Зст на величины корней характеристического уравнения следует, что вращение самолета с Q Ф 0 (при |3СТ ~ 0) приводит к уменьшению величины

—ml и, соответственно, к уменьшению по величине корня крена (см. рис. 16.2), вплоть до появления положительных значений корня. Из соотношения (16.17) следует, что при Орст > 0 прира­щение действительного корня АХ имеет отрицательный знак, т. е. соответствует увеличению степени апериодической устойчивости движения. При QpcT << 0 корень крена убывает по модулю и может изменить знак, т. е. самолет может потерять устойчивость. Рассмотрим, как при этом изменятся остальные корни характе­ристического уравнения. Как следует из (16.5), коэффициент б2 характеристического уравнения не зависит от Й и рст. Учитывая, что этот коэффициент равен сумме действительных частей корней с обратным знаком, получим, что изменение действительного корня приведет к соответствующему изменению действительной части комплексно-сопряженных корней:

Д|= — ±-АХ. (16.18)

Учитывая результаты анализа влияния рст и Q на величину дей­ствительного корня, можно определить влияние этих величин на действительную часть комплексно-сопряженных корней. При QpCT > 0 демпфирование будет ухудшаться, а при £2рст <о демпфирование колебательной составляющей движения будет возрастать.

Как известно, коэффициент характеристического уравнения выражается через корни этого уравнения следующим образом:

51 = т)а + 2$Х. (16.19)

При малых значениях демпфирования коэффициент Вг прибли­женно равен квадрату мнимой части комплексно-сопряженных корней:

if ~ —р (raj) — г асга* + р££22). (16.20)

Как следует из (16.20), с увеличением £2 происходит уменьшение мнимой части комплексного корня, т. е. уменьшение частоты колебаний. На основе проведенного анализа корней характеристи­ческого уравнения, используя терминологию гл. 3, получим, что при малых величинах £2 и |3СТ особая точка обычно является фоку­сом, а при изменении |3СТ и Q может перейти в особые точки (седло — фокус двух типов). Соответствующие иллюстрации приведены на рис. 16.1. В области а) при переходе через бифуркационную гра­ницу происходит изменение знака действительного корня, а в об­ласти в) — знака действительной части комплексных корней.

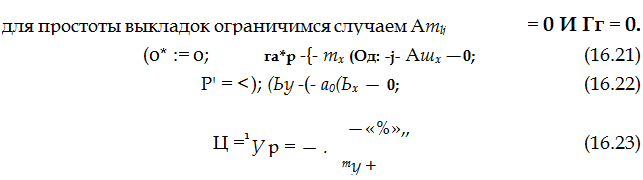Для получения качественного представления о положении фазовых траекторий в трехмерном пространстве переменных (|3, (Ь, 63„) в дополнение к уже найденным параметрам определим изоклинные поверхности, соответствующие нулевым значениям производных ых = 0, |У = 0, (o’, = 0. Из уравнений (15.3) получим соответствующиеТприближенные выражения, в которых

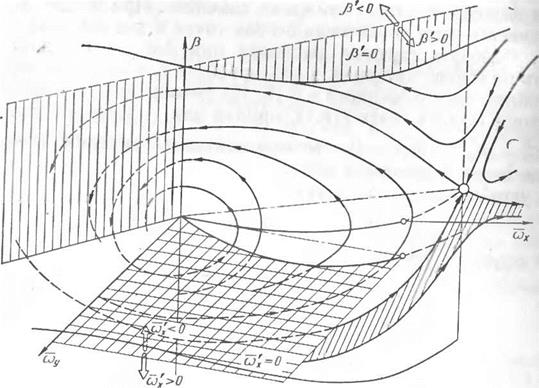
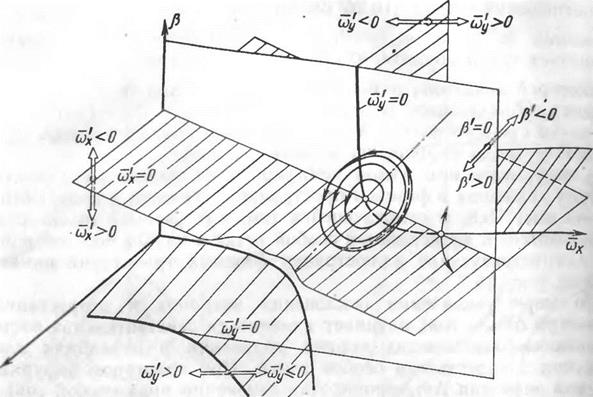
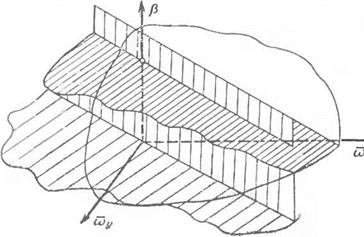
Изоклинные поверхности (16.21) и (16.22) представляют собой плоскости и примеры их расположения в пространстве (р, cov, (Ьу) приведены на рис. 16.3. Значительно более сложный вид имеет изоклинная поверхность (16.23), пример которой приведен на рис. 16.4. Для лучшего понимания расположения этой поверхности

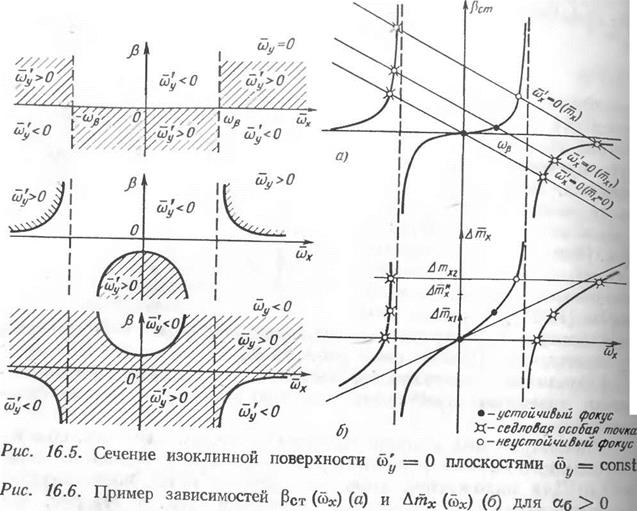
удобно рассматривать ее сечения ПЛОСКОСТЯМИ <0^-=

= const (рис. 16.5). Отме­тим также, что из соотно­шения (16.23) следует: что эта поверхность образова-

Рис. 16.3. Положение изоклин — ных поверхностей й’х = 0 и Р’ =*

OZS О

Рис. 16.4. Изоклинная поверхность

О

на прямыми, проходящими через ось 06)Л и каждой ве­личине со* = const соответст­вует прямая со своим углом наклона. Вид этой поверх­ности не зависит от продоль­ного и поперечного управле­ния. При различной продоль­ной балансировке самолета изменяется положение плос­кости (16.22), а момент Дт* при поперечном управлении приводит к эквидистантному сдви­гу плоскости (16.21) (см. рис. 16.3).

Изоклинные поверхности, вместе с полученными ранее дан­ными, позволяют представить фазовую картину движения само­лета.

Рассмотрим вид фазовой картины движения самолета, сбалан­сированного на положительном угле атаки при управлении элеро­нами. Для нахождения координат особых точек воспользуемся графоаналитической методикой, описанной в гл. 3. На рис. 16.6 приведены примеры зависимостей рст (ш*), Дтх (б)А). Приняв величину Дт* в качестве параметра, рассмотрим как будут изме­няться фазовые картины движения самолета. При малой величине Дт* имеется одна устойчивая особая точка и две седловые особые точки. Фазовую картину движения при Дт* = 0 можно пред­ставить на основе материалов анализа для случая отсутствия демп­фирования, рассмотренного в § 15. Из уравнения для нахождения

координат особых точек (16.1), приняв для упрощения выкладок,

в _ О _ 6)

что == mtj == тху = 0, можно получить значения координат особых точек в конечном виде:

1) устойчивая особая точка

Pi = 0; йх1	= 0; соу1 = 0;	(16.24)
2) седловые особые точки
2, 3 ~	/ 1 1+^1«0 > тх	(16.25)
^у2, 3 = аС^л:2; 3>	—СО-.— т 3 ^2, 3	(16.26)

Пространственное движение самолета пои р

Рис. 16.7. Пример фазовых траекторий для а0 > 0; Атх = Дfhy = 0

Из соотношений (16.25), (16.26) следует, что при уменьшении демп­фирования тхх—> 0, ihyy0, координаты особых точек будут изменяться таким образом, что р2,з 0, а со*2,з может стремиться

к некоторой величине, определяемой отношением тууI тх. Для самолета, обладающего демпфированием, соа2,з > юр — Такие осо­бые точки существовали и в случае нулевого демпфирования при соответствующем подборе начальных условий.

В результате при малом демпфировании можно представить картину движения в фазовом пространстве, близкой к изображен­ной на рис. 15.8, и отличающейся тем, что фазовые траектории «стягиваются» к единственной особой точке в начале осей коорди­нат. Соответствующие иллюстрации фазовых траекторий приве­дены на рис. 16.7.

По мере увеличения отклонений элеронов и возрастания параметра Дтх = Ат* начинает изменяться действительная часть комплексно-сопряженных корней уравнений в вариациях для движения в окрестности особой точки. При некотором бифурка­ционном значении Атх происходит изменение вида особой точки от типа устойчивый фокус в особую точку типа седлофо — кус (см. рис. 16.6) и одно­временно появляется предель­ный цикл (см. гл. 3). Ана­лиз возникающего предель­ного цикла содержится в § 17.

Рассмотрим фазовые кар­тины движения самолета, сба­лансированного на отрица­тельном угле атаки. На рис. 16.8 приведены приме­ры зависимостей рст ((5~) и Атх (со*), позволяющие опре­делить координаты особых то­чек в этом случае. Из анали­за этих зависимостей следует, что при Атх ж 0 имеется три особые точки, одна из кото­рых является устойчивой, и две седловые особые точки.

Рис. 16.8. Пример зависимостей Рст (сох) (а), Атх (со*) (б) для а§ < <0

Рис. 16.9. Пример фазовых траекторий для а0 < О, Атх > О, Artij = О

Движение в рассматриваемом случае имеет вид аналогичный слу­чаю а0 > 0 (см. рис. 16.7).

При увеличении значения параметра Дтх до бифуркационного значения Дга£ (см. рис. 16.8) происходит изменение качественной картины движения — устойчивая и седловая особые точки слива­ются и исчезают, остается только одна седловая особая точка. В этом случае движение самолета в рассматриваемой модели дви­жения заключается во вращении с возрастающей угловой ско­ростью ых. В действительности при учете продольного движения значение со* будет ограничено (см. гл. 7). При дальнейшем увели­чении Дга* и достижении второго бифуркационного значения этого параметра вновь появляются две особые точки: одна — колеба­тельно-неустойчивый седлофокус и вторая — седловая особая точка. В окрестности неустойчивой особой точки реализуется предельный цикл (рис. 16.9). Следует отметить, что свойства фазо­вых картин движения, рассмотренные ранее для нелинейного бокового движения, сохраняются и в общем случае пространствен­ного движения при выполнении условия сор <[ (0а.