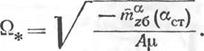. Пространственное движение самолета при <*а С <*>іЗ

В настоящей главе рассматривается второй предельный случай соотношения характеристик самолета, когда меньшей является величина критической скорости крена по тангажу. Аналогично анализу, приведенному в гл. 5, исследования ограничиваются движениями с угловой скоростью крена, удовлетворяющей не­равенству | со* | < со^.

§ 18. ОСОБЕННОСТИ ДИНАМИКИ САМОЛЕТА С МАЛЫМ

ЗАПАСОМ ПРОДОЛЬНОЙ УСТОЙЧИВОСТИ

Рассмотрим свойства пространственного движения са­молета, аэродинамические характеристики которого таковы, что для критических скоростей крена выполняется соотношение

соа<^ е>р. Кроме этого аэродинамические характеристики продоль­ной устойчивости будем как и ранее считать линейными функци­ями своих аргументов. Рассмотрим особенности устойчивости самолета при выполнении маневров крена, обращая вначале основ­ное внимание на влияние силы тяжести на его динамику.

В том случае, когда степень устойчивости самолета по углу скольжения достаточно велика, можно в первом приближении считать, что во все время движения самолета выполняется соотно­шение р ~ р’ ~ 0. С учетом сделанных замечаний запишем урав­нения пространственного движения самолета в следующем приближенном виде:

са

а — рсо2 п=——- JLa k0 (cos у — 1);

— / ——■ ■ ^ ^ СО _

(0Z -j — А)Ш)х(йу ~ “Ь ^z6®z А/7ї20> (18-1)

<йу = — («о + «) tox; р = 0;

У’ litox,

где а — угол атаки, являющийся приращением к углу атаки ссг соответствующему горизонтальному полету самолета;

с™аг

k0 — у-2 cos fh (18.2)

При рассмотрении движения самолета, заключающегося во вращении по крену, выполняемому из условий горизонтального полета, изменения угла тангажа обычно невелики, поэтому во всех случаях будет рассматриваться некоторая постоянная вели­чина Фо» характеризующая в среднем ориентацию траектории самолета относительно Земли. При этих условиях коэффициент kQ является константой и при полете самолета по горизонтальной траектории принимает практически наибольшее значение.

Перейдем к анализу свойств динамики самолета, описываемых системой уравнений (18.1), при его вращении с со* = Q = const. После несложных преобразований уравнения (18.1) могут быть приведены к одному дифференциальному уравнению второго порядка для изменения угла атаки:

— — sin у — (cosy — 1) + Ai2Q2ar, п, (18.3)

где у =

Уравнение (18.3) для а является неоднородным линейным диф­ференциальным уравнением с постоянными коэффициентами и его решение может быть представлено в виде суммы общего и частного решений:

а (т) = D1e£aX cos (оат — j- D2e^aX sin соат — f-

+ C0 — j — Cx cos Q[ix + C2 sin Qp/t,	(18.4)
r ___	+ Ліх29.	(18.5)
L0— —и
cx= v	(«и^л+Н0®!*) . «11 + «12	(18.6)
c — k°		(18.7)
L/ 2 ——	«П +

где

(18.8)
са У 2
(18.9)
,*£>
,ос
(18.10)
?а=-

 

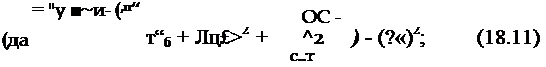Dx и D2 — произвольные постоянные, зависящие от начальных условий.

Для начальных условий а (0) = а’ (0) = 0 постоянные и D2 определяются из соотношений

D1 = —(C0+’Cl );(18.12) : [(О) + ^l) а C2pQ].

В общем случае зависимость изменения угла атаки а (т) при вращении с со* = £2 от параметров самолета достаточно гро­моздка, поэтому для получения наглядных результатов рассмо­трим частный случай медленного вращения самолета, когда Qju, — 0 (в) малая величина. В этом случае приближенное решение для а (т) может быть записано в виде а

а(т) =

(18.13)

 

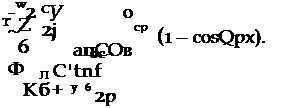Из соотношения (18.13) следует, что:

— изменение угла атаки при крене отрицательное, т. е. угол атаки уменьшается;

— максимальное уменьшение угла атаки будет иметь место при угле крена у ~ 180° и приближенно будет равно:

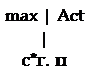2<6^cos^cp

Сї W у

г ^ 2ц

График зависимости величины шах|Да|/аб от параметра 2 ifh^6 построен на рис. 18.1. Из формулы (18.15) и рис. 18.1

 

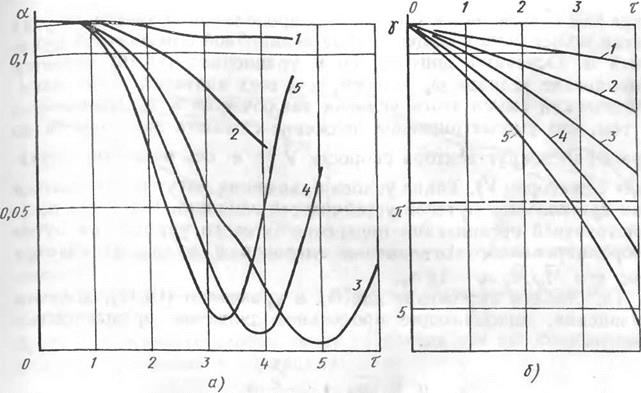
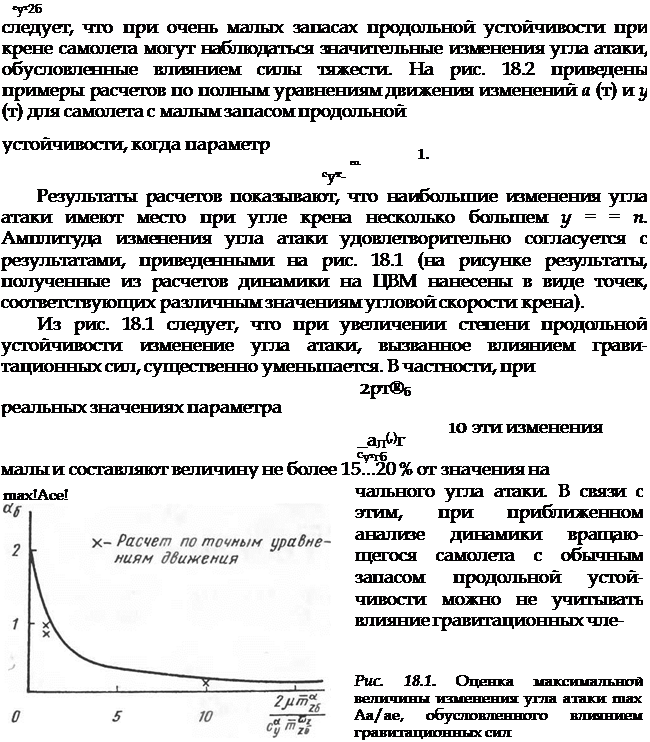
Рис. 18.2. Примеры изменения угла атаки а (т) (а) и изменения угла крена у (т) (б) для самолета с малым запасом продольной устойчивости

нов в уравнениях, что дополнительно подтверждает результаты, приведенные в § 3 гл. 1. Когда степень продольной устойчивости достаточно велика, основное влияние на изменения угла атаки оказывают инерционные моменты, пропорциональные Q2, однако оценка первого минимума в переходном процессе по углу атаки, выполняемая с помощью соотношения (18.15), дает качественно удовлетворительное соответствие, что видно из рис. 18.1. Учиты­вая, что влияние гравитационных сил обычно мало, в дальнейшем основное внимание будет обращаться на влияние инерционных моментов на динамику самолета, а влиянием гравитационных сил будем пренебрегать. С учетом сделанных допущений, уравнения движения самолета (18.1) можно дополнительно упростить и при­вести к виду

— С у

а’ — рш =——- а;

С02 -[- АШ)х^у ■= PP’zt (о&) ~~ МгбЮг (18.16)

СО у == " ^СОд;, Р : — б,

где а — полное значение угла атаки самолета.

В уравнениях (18.16) предполагается, что аэродинамические характеристики су (а) и mz (со2) являются линейными функциями своих аргументов и, следовательно, представляются в обычном

виде как (?уa, ihzza>Zf а зависимость продольного момента от угла атаки может быть в общем случае нелинейной однозначной функ­цией ос. Основным допущением в уравнениях (18.16) является выполнение условия iby = —atox для всех значений угла атаки. Физический смысл этого условия заключается в предположении о том, что рассматриваемое движение самолета заключается во

вращении вокруг вектора скорости V (т. е. ось вращения совпа-

дает с вектором V). Такие условия движения могут реализоваться как при большой путевой устойчивости самолета, так и при соот­ветствующей организации поперечно-путевого управления путем координированного отклонения элеронов и руля направления так, что МУШХ ж —tg а0.

Подставляя выражение для toy в уравнения (18.16), получим уравнения, описывающие продольное движение вращающегося самолета:

а’ — рсо2 =————- |-а;

coz — Areola = тг6 (а) + mzltoz — j — Amz0. (18.17)

Рассмотрим устойчивость решений уравнений (18.17) для различных постоянных величин угловой скорости крена П. Для этого сначала определим координаты особых точек этой системы уравнений при Amz0 = const.

Из (18.17), положив а’ =; toz — 0, получим

toz ст — 2^		(18.18)
— са ^кЬ (^ст) "Ь" — ^СТ 1 ^2б 2|Ц ^ст ——	— Атг0.	(18.19)

В общем случае, когда mz (а) является нелинейной функцией угла атаки, для нахождения связи аст = f (Q, Amz0), необходимо решать нелинейное уравнение (18.19), которое удобно преобра­зовать к виду

tn°zca

тгб (а) + 2^- а + Ат, о == — AiQ*a. (18.20)

Пересечение функции, стоящей в левой части, с линейной функ­цией а в правой части с коэффициентом наклона, зависящим от Q, даст решение. Графическое решение уравнения (18.20) приведено на рис. 18.3.

Для анализа устойчивости движения уравнения (18.17) необ­ходимо линеаризовать относительно параметров движения (аст,

153

і

Рис. 18.3. Пример определения балансировочного угла атаки вращающегося самолета:

а — для линейной зависимости т (а) = таос ; б— для нелинейной зависимости т (ос) 2 2 2

Фгст) в окрестности особых точек. Проведя эти преобразования, получим уравнения в вариациях:

(в уравнениях знак вариации А для сокращения записи опущен). Исходные условия движения самолета вошли в уравнения (18.21)

в виде зависимости локальной производной га? (аст) и входящей в уравнения величины £2. Из (18.21) легко получить характери­стическое уравнение, которое имеет обычный для уравнения ко­роткопериодического продольного движения вид:

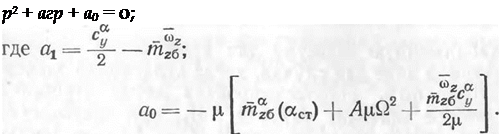(18.22)

(18.23)

Единственным существенным отличием от случая изолированного короткопериодического продольного движения является выраже­ние для свободного члена характеристического уравнения а0, из которого следует, что частота продольных колебаний изме­няется с увеличением угловой скорости вращения самолета по крену £2, и при некотором значении £2 = £2* движение становится неустойчивым. Такое критическое значение £2 = £2* определяется из равенства

Неустойчивость продольного движения при линейных аэро­динамических характеристиках практически не реализуется, так как соответствует (при Дт2 = 0) бесконечно большим баланси­ровочным значениям угла атаки. При нелинейной зависимости mz (а) реализация такой неустойчивости вполне возможна. Рас­смотрим для примера нелинейную зависимость тг (а) ^выпола­скиванием», приведенную на рис. 18.3, б. Самолет при движении с £2 = 0 был сбалансирован на угле атаки аб. При движении с Q Ф 0 балансировочный угол атаки самолета будет увеличи­ваться при возрастании величины Q, и продольное движение будет сохранять устойчивость до тех пор, пока выполняется условие П < Q*. Как видно из рис. 18.3, б, в этом случае может быть три балансировочных значения угла атаки. Первое (точка А) — является устойчивым состоянием равновесия, второе (точка В) — неустойчивое состояние равновесия, и соответствующая особая точка является седловой, а третье (точка С) — также устойчивое состояние равновесия. Движение в окрестности седловой особой точки В неустойчиво, хотя самолет аэродинамически устойчив

(niz < 0) на этом угле атаки. Критическое значение угловой ско­рости крена Q, при превышении которого движение становится неустойчивым (во всяком случае нарушается непрерывная зави­симость между изменением Q и а), определяется из условия, что

при этом значении угла атаки а# локальная производная maz равняется отношению mja^.

Значение угла атаки, удовлетворяющее этому уравнению, позволяет определить критическое значение угловой скорости крена:

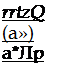
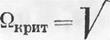(18.25)

Выведем приближенную формулу для критической скорости крена (Оа в размерном виде для случая, когда нелинейная зависи­мость mz (а) может быть аппроксимирована двумя отрезками прямых. Критическое значение момента АМг, при превышении значения которого инерционным моментом (1« — їх) (о£а* насту­пит практическая неустойчивость движения самолета, может быть представлено в виде

АMz = т% (а, — аб) qSbA.

Приравнивая инерционный и аэродинамические моменты и произ­водя необходимые преобразования, получим приближенную фор­мулу для критической угловой скорости крена в размерном виде:

Рис. 18.4. Пример продольного движения на фазовой плоскости сог, а для различных значений угловой скорости крена Q

крит

ляется функцией балансиро — * —х

вочного угла атаки.

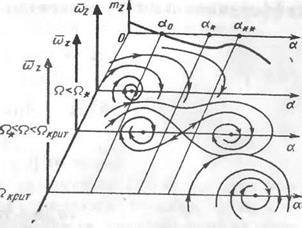
Пример изменения фазовой картины движения для различных величин со* — Q для характеристики mz (а), имеющей «ложку» на больших углах атаки, приведен на рис. 18.4. Видно, что при £2 = 0 имеется одна устойчивая особая точка. По мере увеличе­ния угловой скорости крена сначала дополнительно появляются две особые точки — седловая и фокус, а затем седловая особая точка сближается с устойчивой особой точкой, и при Q = QKpllT они исчезают. Остается одна особая точка типа устойчивого фо­куса.