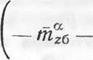ВЛИЯНИЕ ПОПЕРЕЧНОЙ УСТОЙЧИВОСТИ НА ПРОСТРАНСТВЕННОЕ ДВИЖЕНИЕ САМОЛЕТА С МАЛЫМ ЗАПАСОМ ПРОДОЛЬНОЙ УСТОЙЧИВОСТИ

В § 18 в качестве первого приближения анализ ограни-

чивался движением самолета, при котором угловая скорость крена предполагалась неизменной величиной. Однако даже в слу­чае достаточно большого запаса путевой устойчивости в процессе возмущенного движения при вращении самолета происходит изме­нение угла скольжения, которое при достаточно большой вели­чине поперечной устойчивости самолета может оказывать влияние на его движение. В этой связи в настоящем параграфе в качестве второго приближения рассматривается влияние изменения угла скольжения самолета на его динамику по-прежнему в предполо­жении, что степень продольной устойчивости самолета значи­тельно меньше его путевой устойчивости, т. е. ба Юр. При этом ограничении на характеристики рассматриваемых самолетов, осно­вываясь на методике понижения порядка дифференциальных уравнений (§ 3), можно приближенно находить угол скольжения самолета из квазистатических соотношений, считая, что во все время движения моменты относительно оси 0Y самолета в среднем являются сбалансированными. При рассматриваемых предполо­жениях движение самолета будет описываться следующей системой

Пространственное движение самолета при o^-egco),

СС г

дифференциальных уравнений:

а = роз.

а — р(Зсох;

toz — т%а — /1рсо*а)/у — f — mz£toz — f — Дшг;

(19.1)

 

Wlyfy |~ ^ у езу -—- О,

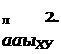
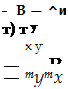
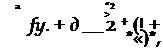В уравнениях (19.1) под величиной а понимается полное значение угла атаки самолета.

После простых преобразований система уравнений (19.1) при­водится к виду:

„а

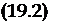03z ~— ~f" і4рс0л;ОС — j- Шг^,С0г Af^zO»

—’ _ G) — _

03л; шх (1 — J — Ьа) сох ~(- A/?z#o у

(19.3)

Определим из системы уравнений (19.2) координаты особых точек в зависимости от величин управляющих моментов Дтх и t±thy. Приравняв производные параметров движения нулю, после простых преобразований получим нелинейное алгебраиче­ское уравнение для угла атаки, нули которого дадут значения а в особых точках:

(19.4)

(19.5)

Координаты других параметров движения в особых точках при известных значениях а = а* определяются из выражений

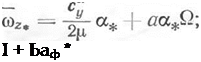(19.6)

(19.7)

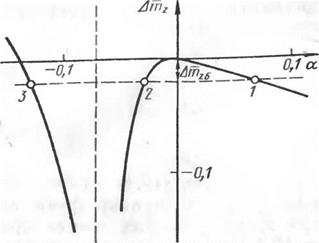
Нахождение нулей нелинейного уравнения (19.4) удобно вы­полнять графически. На рис. 19.1 построен пример функции F (а) и определены значения угла атаки в особых точках при некотором значении Atnz. Из рис. 19.1 следует, что при рассма­триваемых значениях Ага* и Amz имеются три особые точки (/, 2, 3). Причем движение в особых точках 1 и 2 происходит с угло­вой скоростью крена со*, совпадающей по знаку с моментом Am*, создаваемым органом поперечного управления, а в особой точке 3, движение происходит в направлении, обратном моменту т*, что обусловлено действием на самолет момента поперечной устойчи­вости.

Определение координат особых точек можно было выполнить, используя общую процедуру, описанную в гл. 3. Для этого необходимо построить зависимости функций аст (со*), Рст(й>*) (рис. 19.2), соответствующие установившемуся движению и задан­ной величине Amz, с помощью которых строится зависимость по­требного момента поперечного управления, позволяющего реали­зовать движение с соответствующей величиной со* (рис. 19.2, в). Из графика на рис. 19.2, в при заданной величине Ат* находятся значения о)*, позволяющие определить значения остальных пара­метров движения в особых точках. Из анализа зависимости Ат* (со*) с учетом условия апериодической устойчивости (10.8),

(10.9) , следует, что особая точка 1 является устойчивой, а особые точки 2 и 3 являются неустойчивыми, так как в них характери­стическое уравнение имеет положительные корни. Для более подробного анализа движения в окрестности особых точек лине­аризуем уравнения (19.2) относительно соответствующих этой

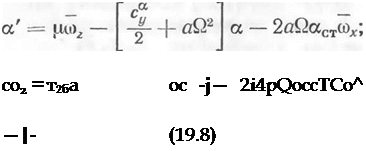особой точке параметров движения (£i, аст, coZCT). Опуская для сокращения записи знак приращения, получим уравнения в ва­риациях:

со* а тх * (1 т) to* ffix bQoc.

Пространственное движение самолета при

Рис. 19.1. Определение значений угла атаки в особых точках для заданных величин Amx, Amz

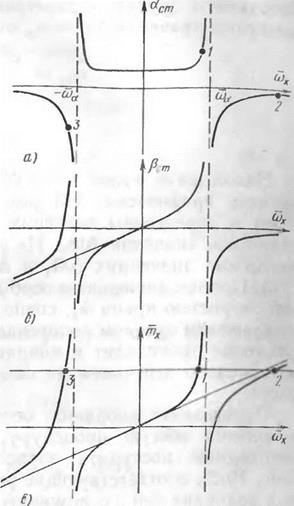Рис. 19.2. Нахождение параметров движения аст, рст, йх, в особых точках

для заданных величин Aihx, Athz (rm% = — const)

Характеристическое уравнение системы линейных уравнений

(19.3) имеет вид

р3 + D2p2 + D±p + D0 — О,

а — —

Си _ oz _ о)х

где D2 = ~——— тг6 —тх (1 + Ьасг);

а

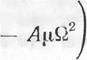
— тЦх (1 + ЬаСТ) (-#— mil) — 2аЬт<1,:аСт^~> (19. Ю)

Do = nil* (1 + baCT) І (і ( mSs +

~2Aii2Q2thxxba„ 4- 2abmlxfnlZQ2ает*

При малом значении аст характеристическое уравнение (19.9) приближенно может быть представлено в виде произведения двух полиномов:

Приравнивая нулю каждый из полиномов, можно получить при­ближенные выражения для корней продольного движения и дви­жения крена. Анализ значений корней в особых точках показы­вает, что в особой точке 2 один из корней продольного движения становится положительным, а в особой точке 3 — положительным становится корень крена.

Для построения схемы движения в фазовом пространстве рассмотрим положение изоклинных поверхностей, соответству­ющих нулевым значениям производных параметров движения.

Уравнение поверхности со* = 0 может быть представлено в виде

Это уравнение цилиндрической поверхности с образующей парал­лельной оси Ocoz, которая при пересечении с плоскостью coz — О образует гиперболу. Из уравнения для а получим изоклинную поверхность, на которой а = 0:

При малых значениях со* эта поверхность является плоскостью,

проходящей через ось Осо*. Используя знания о положении и виде изоклинных поверхностей и свойствах движения в окрестности особых точек, можно представить схему движения для рассма­триваемого случая в фазовом пространстве (рис. 19.3). і

Движение в окрестности особой точки 3 в зависимости от начальных условий развивается различно. Часть фазовых траек­торий имеет точкой притяжения особую точку У, а другая часть соответствует неустойчивому движению с неограниченным воз­растанием параметров (в рамках рассматриваемой упрощенной модели движения).

Воспользовавшись методом, изложенным в гл. 3, определим уравнения сепаратрисных плоскостей в окрестности особых точек, соответствующих значению действительного корня X характери-

Рис. 19.3. Схематическое изображение фазовых^ траекторий в пространстве (а, (дх, c5z) и положения изоклинных поверхностей (Ох = 0 и а =0

стического уравнения. Уравнение сепаратрисной плоскости можно записать в виде (см. § 17)

a (W + а" + а’ (к2 + %3) = 0. (19.14)

Учитывая, что

^зЛг^з ~ Do]

^1 ^2 “Ь ^3 “ —- Т)2*

произведем замену в уравнении (19.14):

Я2Я3 = — —■ ; (19.15)

^2 + ^3 = —— (D2 + ^l),

I

получим:

— а + а" — а’ (D2 + Я,) = 0. (19.16)

Выразим а" и а’ через параметры движения о^со*, со*. Для полу­чения обозримых результатов пренебрежем в уравнении для а

„а

—2 С,,

членом сш*а, который обычно значительно меньше, чем -~-а

(составляет менее 10 °о от этого члена). С учетом этого упрощения, получим:

— са

а’— рок——— |^-а; (19.17)

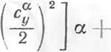а

‘У
рпг 2б — ц	(19.18)
+

 

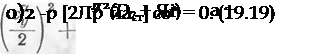Подставим в (19.16) выражения (19.17), (19.18) и проведем необ­ходимые преобразования:

Уравнение (19.19) является уравнением сепаратрисной плоскости в окрестности особой точки.

В случае существенной зависимости поперечной устойчивости т* от угла атаки, когда момент крена, вызванный углами а и р, приближенно можно представить в виде га*роф, уравнения дви­жения имеют вид, аналогичный (19.2), кроме уравнения для со*:

са

/ — ь —2

a = резг——— — ашдх

* —- /72* (1 -р Ь+а ) со* — р — Д/и*,

ь. = тТГщу jmlnt.

Координаты особых точек в этом случае могут быть найдены из алгебраических уравнений

СОлсО.

I + 6*а2 ’

Рис. 19.4. Нахождение параметров движения аСтэ Рст, в особых точ­ках для заданных величин Ат*,

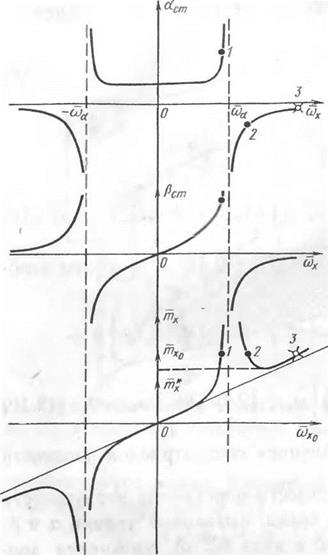Amz (т£ == tri^a)

Опр едел ить коорди наты особых точек можно, решая графически нелинейное ал­гебраическое уравнение (19.22) либо используя стан­дартную методику, изло­женную в гл. 3. На рис. 19.4 приведены зависи­мости аст (со*), рст (со*) и следующая из уравнения для

со* = 0 зависимость Д/п*(соА). Из приведенных на рис. 19.4 графиков следует, что в за­висимости от величин откло­нения органов управления в фазовом пространстве пара­метров движения самолета возможна либо одна особая точка, соответствующая устойчивому движению, либо три особые точки, две из которых 1 и 2 соответствуют устой­чивому движению, а особая точка 3 является седловой и соот­ветствует апериодически неустойчивому движению.

В рассматриваемом случае систему уравнений (19.20) можно

дополнительно упростить, приняв, что уравнение для со* выпол­няется квазистатически. Это допустимо сделать, поскольку, как следует из последнего уравнения системы (19.20), движение

по со* устойчиво при любых значениях а. Следует отметить, что

при аналогичном анализе динамики самолета с raf = const при достаточно больших отрицательных значениях угла атаки дви­жение крена становилось неустойчивым и это не позволяло пре­небрегать динамикой изменения угловой скорости крена. При пренебрежении этим движением из учета выпадает неустой­чивый корень крена, что приводит к качественно неверным вы­водам.

Рассматривая изменения со* как квазистатические в соответ­ствии с соотношением (19.21) и для упрощения выкладок отбрасы­вая член ясо* в уравнении продольных сил, который мал, получим
приближенное уравнение для нахождения фазовых траекто­рии:

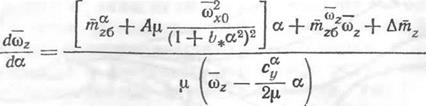(19.23)

Из системы уравнений (19.20) получим уравнение изоклинных кривых. Из условия а’ = 0 получим уравнение прямой:

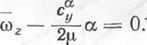(19.24)

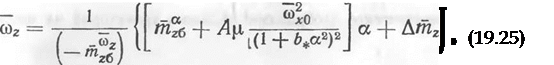Уравнение изоклины, на которой со* = 0, имеет более сложный вид:

На основе знания изоклин и характера движения в окре­стности особых точек можно представить схему фазовой картины

движения на плоскости (а, со2) (рис. 19.5).

Фазовая картина движения может быть уточнена, если вер­нуться к анализу движения в фазовом пространстве. Из послед­него уравнения (19.20) получим уравнение изоклинной поверх­ности сох = 0:

tnx (l bjx ) (х)х “I — A#z* — 0.

Из (19.26) следует, что изоклинная поверхность, на которой со* = 0, является цилиндрической поверхностью с образующей, параллельной оси 0о2, симметричной относительно оси а = 0.

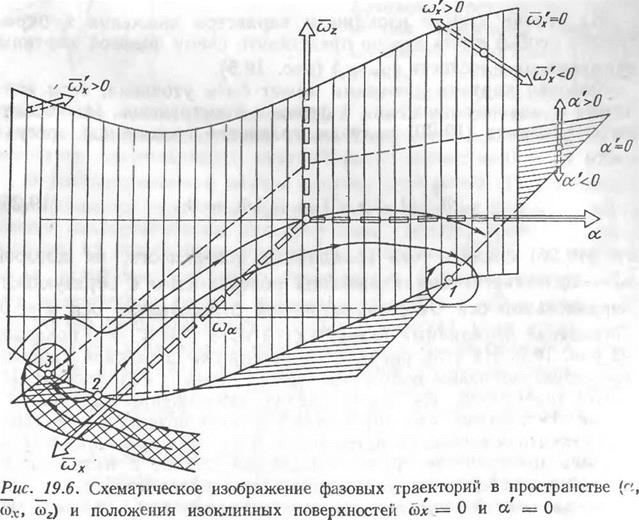
Положение изоклинных поверхностей со* = 0 и а’ = 0 показано на рис. 19.6. На этом рисунке приведена схема фазовой картины движения, показаны положение особых точек и направление фа­зовых траекторий. Из сопоставления изображений на рис. 19.6 и рис. 19.5 видно, что упрощенный анализ позволил правильно представить основные свойства фазовой картины движения в трех­мерном пространстве. Более подробный анализ с нахождением корней характеристического уравнения и уравнений сепаратрис — ных плоскостей может быть выполнен методом, аналогичным

I

Влияние поперечной устойчивости при уменьшенной продольной устойчивости 165 изложенному ранее при анализе случая m* = const. Отметим, что запись уравнения сепаратрисной плоскости (19.19) сохранится

и в случае, когда /Пх зависит от угла атаки. При вычислении коэф­фициентов в этом уравнении необходимо только подставлять соответствующее значение действительного корня.

Из полученных в настоящем параграфе результатов следует, что анализ, выполненный в предположении, что |3 = 0 (§18), ограничивается исследованием движений только в окрест­ности особой точки I (см. рис. 19.3, 19.6), т. е. движением

с со* < соа.