РАСЧЕТ СТАЦИОНАРНОГО КОНТУРА ТЕЛЕУПРАВЛЕНИЯ ПО КРИТЕРИЮ МИНИМУМА ДИСПЕРСИИ ПРОЛЕТА

Ранее рассматривались задачи оптимального управле­ния, в которых не фиксировалась заранее принадлеж­ность закона управления к какому-либо классу динами­ческих систем.

Здесь мы предположим, что система телеуправления в целом принадлежит к классу линейных динамических систем с постоянными параметрами и конечной памятью, и рассмотрим задачу определения импульсной переход­ной функции системы в этом случае.

В качестве воздействия на контур телеуправления рассмотрим линейную координату

ha{t)=h0—h, f^—, (3.96)

измеряемую с ошибками n(t), являющимися стационар­ным белым шумом с характеристиками

M[n{t)=0, М{п{^)п(^)]=М Щ — tJ. (3.97)

Обычно h0 и ho, характеризующие начальные ошиб­ки процесса телеуправления, неизвестны априори и из­меняются в широких пределах, а ускорение / ограничено.

Выходной координатой контура будем считать про­лет Rv(t).

Рассматривая процесс на выходе при значениях вре­мени t, больших памяти Т системы, получим

ЯР(і)=№ 0] dx. (3.98)

о

Ошибка системы согласно уравнению кинематических связей (1.70) может быть записана в виде

Я(*)=*0(А+М*)-| *(т)[А,(*—т) + я(/—т)]Л, (3.99)

то случайная составляющая ускорения определяется со­отношением

№~г

*ос

Подставляя выражение (3.104) в уравнение (3.107) и применяя формулу интегрирования по частям, полу- чим при условии II о т •9 (3.108) hW=MdJ7rnV-T)dx- *ос щ) dT 0 (3.109) Дисперсия ускорения с учетом уравнений (3.97) определяется выражением (3.109) и Осо (ЗЛЮ)

Заметим, что условия (3.108) необходимы для конеч­ности дисперсии ускорения Dj при белом шуме n{t).

Ограничение дисперсии ускорения при синтезе конту­ра телеуправления может быть учтено с помощью не- равенства т |*W (3.111) При этом NC, (3.112) toc

Рассмотрим задачу определения импульсной переход­ной функции k(x) стационарного контура телеуправле­ния* минимизирующей дисперсию пролета в виде выра­жения (3.105) при условиях (3.102) и (3.111) [24].

Условие оптимальности (2-. 135) в этой задаче примет вид

— + *(t)+<и — tiT + 1*2Т*=°* (3.113)

где ф0, фь фг. фз. Ф4 — неопределенные множители Лаг­ранжа, определяемые из условий (3.102) и (3.111).

Дифференциальное уравнение (3.113) определяет k(x) в интервале 0<т<Г при граничных условиях (3. 108)

k(Q)=k(T)=0.

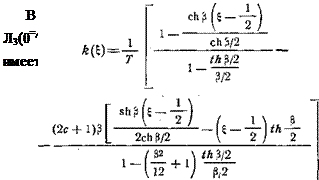Здесь обозначено

На рис. 3.1 представлены графики k(Q для различ­ных условно принятых значений параметра р, характе-

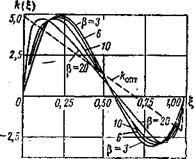Рис. 3.1. Импульсные пе-
реходные функции &(£)
при различных диспер-
сиях ускорения

ризующего степень ограничения дисперсии ускорения А с = 0,1. Для сравнения приведена импульсная переходная функция. Йонт (£) системы, рассчитанной без учета огра­ничения (3.111):

Кт W = — f [т “ 5 + • (1 ““ 25)} (3- 116)

п

На рис. 3.2 представлены относительные дисперсии ускорений

DjT

~N~

t

в функции параметра р, а на рис. 3.3 — относительные дисперсии пролета

drt

N ‘

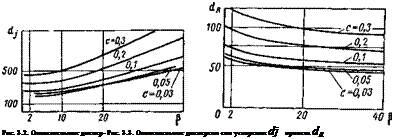
Приведенные графики свидетельствуют о существен­ной зависимости дисперсии ускорения от параметра р и

возможности существенного уменьшения дисперсии уско­рения при незначительном уменьшении дисперсии про­лета.

При р—мэо условия оптимальности в виде уравне­ния (3.113) соответствуют контуру телеуправления, обеспечивающему минимальную дисперсию ускорения при заданных моментных условиях (3.102). Отметим, что в этой задаче дисперсия пролета несущественно (на 20—30%) возрастает по сравнению с системой, не учитывающей ограничение дисперсии ускорений. Отсюда следует возможность расчета контуров теле­управления по критерию минимума дисперсии ускорения при заданном динамическом пролете. Полученный в этом случае контур может обеспечить заданные динамиче­ские ошибки при минимальном расходе управляющих сил [27].