Многомерные задачи оценивания

Совместное оценивание ряда параметров или проверка статистичес­ких гипотез относительно совокупности этих параметров составляет содержание многомерных статистических методов. Один из подходов к решению данной задачи заключается в построении доверительного интервала для каждого из исследуемых параметров, характеризуемых доверительной вероятностью у/, такой, что совместное нахождение истинных значений параметров в соответствующих доверительных интервалах выполняется с заданной вероятностью у3 = Лу/, /= 1

В общем случае совместная доверительная вероятность у связана с доверительной вероятностью по каждому из параметров в отдельно­сти неравенством Бонферрони:

уї: 1-Х (1-у,), 1-у,- £(1 —у3)/£.

/=1

При независимости исследуемых параметров общая доверитель-

к

ная вероятность у = П у,-, откуда у,- = (уу3.

При коррелированных параметрах для определения у;- применяет­ся метод Тьюки, согласно которому

у>Р[тах|^/|<^(А:,л-1)], 1<і<к,

Ъ — Mz- — —

где U: = ——, V1J — статистика Стьюдента; ъ, б[г,1 — оценки наи — меньших квадратов; Uy(k, n-1) — квантиль распределения максиму­ма абсолютных значений к стьюдентовских статистик.

При известном коэффициенте корреляции между любыми пара­ми параметров общая доверительная вероятность где U§ (к, я -1) — квантиль распределения максимума абсолютных зна­чений к стьюдентовских статистик с учетом коэффициента корреля­ции.

Доверительный интервал на каждый из параметров при использо­вании ДаННОГО ПОДХОДа Определяется ИЗ СООТНОШеНИЯ Zi ] •

В табл. 10.8 приведены значения квантилей l/(i_y(.)/2 для у3 = 0,95 в одно — и многомерном случаях. Рекомендуется выбирать метод, обес­печивающий наиболее узкие доверительные интервалы.

Таблица 10.8 Значения Щі-у,)/2 для g3 = 0,95 в одно — и многомерном случаях при использовании различных методов к Независимые параметры Неравенство Бонферрони Метод Тьюки (л = 60) Р =0 Р=0,2 Р = 0,4 Р = 0,5 1 1,64 1,64 1,64 1,64 1,64 1,64 10 2,58 2,58 2,64 2,61 2,55 2,5 20 2,75 2,82 2,88 2,85 2,77 2,71

При использовании многомерного подхода общая достоверность решения, определяемая ошибками первого и второго родов, суще­ственно снижается. Например, для независимых параметров имеем:

« = 1- П (1-а/); р = 1-П(1-р,).

1 = 1 1=1

Поэтому в практике проведения испытаний существует тенденция использования обобщенных параметров, являющихся некоторой из­вестной функцией одномерных параметров. При выборе такого обоб­щенного параметра строится доверительный интервал на этот пара­метр. Такой доверительный интервал оказывается, как правило, более узким, чем при применении первого подхода, однако не позволяет обнаружить, по какому именно частному параметру не выполняются требования.

Для подтверждения требований к совокупности параметров удоб­но использовать комбинацию указанных подходов: сначала проверка ведется по обобщенному параметру и в случае несоответствия требо­ваниям производится анализ каждого из показателей в отдельности.

Проверка по обобщенному параметру может осуществляться с ис­пользованием ^-критерия Хотеллинга. Если в одномерном случае

ние, то по аналогии для оценок ZT = |q,…,Z2| векторного параметра 0Т = |0| 0* строится Т2- критерий Хотеллинга:

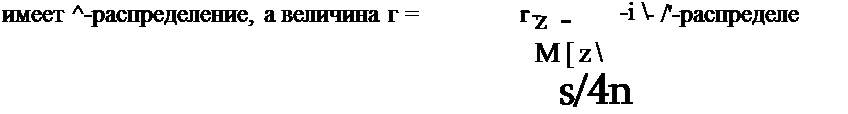для нормального распределения случайная величина / =

Т2 = n(Z-М) СУ2) (Z-M),

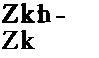где S2 = —— ZTZ — дисперсионная матрица; п -1

Мт = ||Л/1,…,Л/*|| — строка средних значений параметров.

Если верна нулевая гипотеза М — , то статистика Т2 ■

к(п -1)

имеет распределение Фишера F(k, п-к) с к, (п-к) степенями сво­боды. Для оценок некоррелированных параметров ^-критерий можно упростить:

Критерий Iі можно использовать как непосредственно, так и для построения критерия подтверждения требований к обобщенному параметру д, представляющему собой линейную комбинацию одно-

к

мерных параметров: О = ^Х>|0|, где — весовые коэффициенты. В

/=1

d-A/Tdl к к

этом случае статистика ————- где Ь = ‘ZKz,, Ш>] = 2>,Л/,,

i=1 ,=i

к

ст2^] = , будет иметь распределение Фишера. F(l,/j-l) =

= /2 (я -1) .

Таким образом, легко построить доверительный интервал на обоб­щенный параметр Более сложным является слу­

чай нелинейной зависимости обобщенного параметра от одномерных параметров: = 6(01(…, в* ).

По аналогии с линейным случаем можно построить оценку

(«О*

д = б(в) • Моменты этой оценки определяются по следующим соот­ношениям:

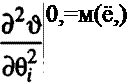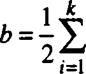Нетрудно показать, что при нормальных законах распределения оценок одномерных параметров оценка обобщенного параметра так­же нормальна, однако имеет смещение

Действительно, для нормального распределения третий и чет­вертый моменты соответственно равны |х3 = 0, |х4 = За4. При

зс4(ё()+бЦ <•=1 у=1 і* І

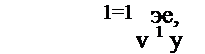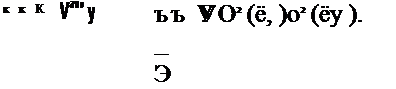(13(0,) = 0, |Хз(‘0) = О, т. е. равен нулю. Четвертый момент

о2*]-!

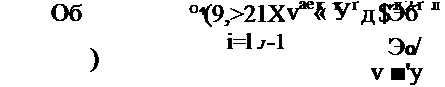Заметив, что

получим ц4 [о] = За4 I’d] • При проведении расчетов неизвестные зна­чения м Гё,- 1 заменяются обычно их оценками ё,- ■

Исследования точного (когда оно существует) и приближенного решения показали, что приближенная дисперсия всегда не меньше, чем точная (равенство достигается в линейном случае). Эго дает оп­ределенную гарантию того, что достоверность принимаемых на основе приближенного подхода статистических решений будет несколько за­нижена.