ПРИ ЭКСПЛУАТАЦИИ

Перейдем теперь к построению алгоритма, который в соответст­вии с требованиями, сформулированными в § 6.1, должен обеспе­чить корректировку значений элементов МВП на основе дополни­тельной информации в виде распределений результатов измерений. по состояниям области работоспособности. Для лучшего понима­ния идеи такого алгоритма изложим ее на примере корректиров­ки элементов МВП эргодической цепи [17], а затем обобщим на •случай цепи с поглощением.

Рассмотрим параметр, который аппроксимируется эргодической iiciii. io Маркова 1-го порядка и имеет область определения, разде­ленную на F нелересекающихся отрезков — состояний 1, 2,…, F. Пусть в моменты времени х— 1 ит получены п независимых по — (дедовательноетей измерений. Оценки вероятностей переходов, най — ii’iHiwe методом максимума правдоподобия, имеют вид (6.2), а зна­чении оценок безусловных вероятностей пребывания аз момент т в. ( ос гоянии i, 1= 1, 2,…, F

Ч± (т)

F F

2 S "і* (Т)

5=11=1

пи н|Я (т)—количество реализаций, зафиксированных в момент т в состоянии’ S При условии, ЧТО В момент X—1 исходное состояние было Г, Пі (т) — коли­чество реализаций в момент т в состоянии І.

I Із условия нормировки ясно, что

F

2 п’і <т) =1

1=1

II редполоясим, что В очередной момент времени Т+1 по резуль­татам контроля МОЖНО оценить ТОЛЬКО величины яДт+1), / = 1,.

.., Г. Для рассматриваемой эргодической цепи должна удовле — I икриться система уравнений

F

2«і(*)*іуМ-я,(т+1)~0, у = 1,2,…,F. (6.16)

i=i

Однако если безусловные вероятности Яг(т) и яДт+1) в урав­нениях (6.16) заменить их статистическими оценками я/(т) и л,'(і | 1), то в общем случае равенство нарушится. Пусть сущест­вуют поправки Aqa (т) такие, что (6.16) .выполняется. Тогда

2 Пі (х)Яч (т) +bQu (т)] — л’і (т +1)=°- (6- 17)

1-і

( Kid значим q’ij (т)+Agij(x) =уц{х+1). Наложим условия, с уче­нім которых следует выбирать поправки Aqa(x). Вследствие того,, •пн і/,,(т+1) — условные вероятности, они должны:

мыть неотрицательными, т. е. ^іі(т+1)>0, і, j= 1, 2,…, F удовлетворять требованию, накладываемому на элементы стро­ки стохастической матрицы

F

2‘Мт+,)-1=°* Т7; (6.18)

і=і

удовлетворять системе уравнений (6.17) существования эрго- ппчегкоп марковской цепи.

Гак как количество независимых уравнений (6.17) и (6.18) меньше числа неизвестных, то существует бесконечное множест­

во значений 9jj(r+l), удовлетворяющих этим условиям. Чтобы уменьшить неопределенность, выберем поправки Aqij(i) так, что­бы минимизировать квадратичную форму

£* = 22 кч(г + 1)-^і(т)]2=тіп

/ТіуТі {9«7(т+1)}

i=i

F

^^COtf/yCr+l) —я}(т + 1)=0. І—1,2,…,/г;

і[3]

<7/у(т+1)>°> ЧУ’ЄЇ,/7.

Сформулированная задача (6.19), (6.20) относится к классу за­дач квадратичного программирования, для которых имеются алго­ритмы решения [63]. Выбор целевой функции в виде квадратичной ‘формы (6.19) не является единственно возможным, есть другие ва­рианты:

22м*+і)-*/мі;

І І

Однако их исследование является самостоятельной задачей.

Результатом решения будут оценки элементов матрицы вероят­ностей перехода, вычисленные с учетом дополнительной информа­ции в виде безусловного распределения по состояниям марковской цепй в момент т-г 1.

При решении описанной задачи существенным является вопрос о целесообразности уточнения оценок. Он обусловлен тем, что зна­чения я/(тЧ-1) являются статистическими оценками вероятностей Яз(т+1), и, следовательно, нарушение равенства в системе уравне­ний (6.16) будет определяться, с одной стороны, существенными различиями в значениях qij в моменты т и т+1, и, с другой—.пог­решностями вследствие конечности числа измерений.

Обратимся к системе уравнений (6.17) и преобразуем ее к сле­дующему виду:

F

2я,-(т)Д^,7(т)=Яу(т+ 1) — яу(т + 1), у = 1,…,F, (6.21)

1

F

tj-дея}(т + 1) = 2я;(т17;у(т)— прогнозируемое значение Яі(т-Ні): я/(т+1) — г=)

оценка по результатам измерений.

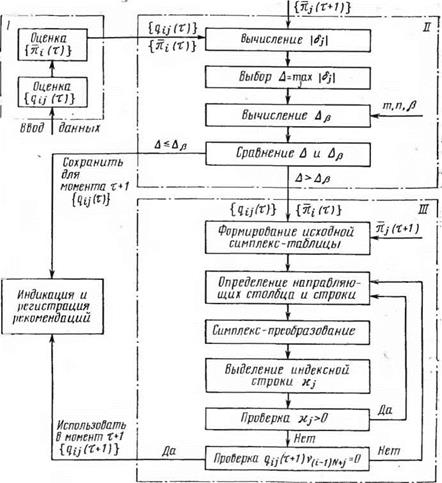
I‘iif (>.l. Блок-схема алгоритма оценки и уточнения значений вероятностей пере­мити цепи Маркова

частей. В части I осуществляется оценка по методу максимума правдоподобия с использованием выражений (6.2) и (6.15), во II части проверяют целесообразность уточнения вероятностей перехо­да на основе критерия Смирнова. III часть представляет собой ал­горитм квадратичного программирования, позволяющий решить задачу (6.19), (6.20). Остановимся более детально на работе час­тей II и III. Целесообразность уточнения qij проверяют следую­щим образом. Рассматриваются две гипотезы: Я0 — распределения л/(т+1) и 3tj(T+l) статистически не отличаются; Я,— различия в распределениях я/(т+1) и я;; (т +1) существенны. Для всех j вы­числяются модули разности!6j! = |я/(т+1)—Яз(т+1)| и опреде­ляется Д = гпах!8у|.

і

При заданном уровне значимости р вычисляется Лр = =l/ln p[(m+n)/2mn], где т, п — количество реализаций, по кото­рым оценивались значения Яі(т+1) и я/(т+1).

Если Л>Др, то гипотеза Яо отвергается, и, следовательно, необ­ходимо продолжать уточнение оценок Цц. Если Д^Др, то гипотеза Я0 считается верной. Тогда для использования в момент т+1 выби­раются значения qij, найденные в предыдущий момент т. Получе­ние такого результата не должно исключать последующие провер­ки гипотез Н0 и Нъ После ввода новых значений яДт+в), s>l не­обходимо по-прежнему использовать II часть алгоритма, так как возможно появление значимого различия (6.21). (

При решении задачи квадратичного программирования исполь­зуется метод множителей Лагранжа [63]. После приведения целевой функции (6.19) к стандартному виду (смена знака) функция Лаг­ранжа

£=-2 2 fo"-(T+ 1)-^^)]2+2х‘- (І

І-1 у-1 /=1

+2 xF-i+j (2Яі w Чи (т+!) — l«=i

где Кі — множитель Лагранжа.

На основе теоремы Куна-Таккера [63] получаем необходимые ус­ловия для седловой точки:

——j-——— —2 дп (тг -+-1) — <7и (т)] +^і "С 0;

00и(* + I)

——-1—— ——2 [<7,2 (f 41)—912(f)] +^і+^+іяі (г) ^>0; 0012(^+1)

-—7——- —= —2 [qi} (т + 1) — qu (f)] +^i 4" V+7-in< (т)

00І.7 С11 + *)

2 qFF (f 41) — Qff (f)] 4’4r4 ^2 f — ^F(r)<0;

для всех г = Г,…., 2 F—Г

(см. исходные условия задачи).

Введем свободные переменные v(v^O) и преобразуем смешан­ную систему (6.22) в систему равенств:

2<7и (f +1) — 2^п (т);

^Яц (f + 1) — К — — *f-1+7% (г) — «(,_!) Ґ+/ = ‘2qi j (t);

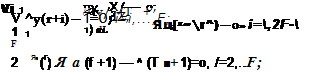2^f (т — f-1) — — X2F — lnp{X) V2F — %1ff(.x) !■

F

2^(t+1)~1=0’ i =

j=1 F

2 яг M я a (f + 1) — Я; (r + 1) = 0) j = 2F.

1 г-і

При этом необходимым условием выбора свободных перемен­ных является равенство нулю произведения 0tv(T+l)0(i-l)F+J для.

Ill-сX / И /.

Теперь задача сводится к нахождению допустимого базисного решения полученных систем уравнений (6.23), (6.24). Воспользуем­ся для этого методом искусственного базиса. Введем искусственные переменные tji и образуем псевдоцелевую функцию

і и- М произвольно большое число; т — число искусственных переменных

И,’ 0.

Дальнейшие стандартные симплекс-преобразования совместной системы уравнений определяют допустимое базисное решение, ко — трое при отсутствии в базисе искусственных переменных и выпол­нении условия 9іі(т+1)°(гЫ)Г13 = 0. г’> является оптималь-

MUM Результатом решения является откорректированная матрица переходных вероятностей марковской цепи.

Проиллюстрируем работу описанного алгоритма на примерах.

Пример 1. Пусть в момент х по т—100 реализациям были получены оцен — • ки максимального правдоподобия

/0,400 0,400 0,200ч! І?;/(т)ІІ= (0,660 0,300 0,100 j,

,100 0,100 0,800/ а вектор {лі(т)} = {0,300; 0,600; 0,100}.

В момент т Ь I оценки значений вектора {Яу (т Ь 1)} были получены на осно­ве п== 50 измерений и составили {Лу(т -|- 1)} = {0,100; 0,400; 0,500}. Прогнози­руемые значения вектора {Яу (х + 1)} ={0,490; 0,310; 0,200} и соответственно {ЪА = {0,390; 0,090; 0,300}.

При Э = 0,1, т — 100, п= 50

Тогда Д max ]6j| =0уЗЮ>Д3=Ю,19, т. е. необходимо уточнить значения і

переходных вероятностей в момент т+1. Результаты расчета по алгоритму квадратичного программирования имеют вид

/0,291 0,390 0,319 (т + 1)|1= ( 0 0,477 0,529

,129 0 0,871

Пример 2. Приведем только окончательные результаты расчетов для мат­рицы 4X4: /0,400 0,200 0,200 0,200 1 0,300 0,100 0,100 0,500 \QU (*)!■ ~1 0,800 0,100 0,100 0 0,600 0,200 0,100 0,100 я,- (т)} = {0,300; 0, 200; 0, О О о 400).

Если {Яу(т + 1)}= {0,100; 0,400; 0,400; 0,100}, то

И) 0,412 0,393 0,195л

0 0,506 0,494 0

ІІ9,/7(т +1)11=| о 0 0,583 0,417

0,250 0,438 0,312 О

Таким образом, использование дополнительной информации в виде безус­ловных распределений позволяет уточнять переходные вероятности цепей Марко­ва 1-го порядка.