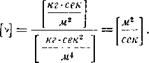
. АТМОСФЕРА. КРАТКИЕ СВЕДЕНИЯ О СТРОЕНИИ АТМОСФЕРЫ

В настоящее время имеются достаточно полные (с точки зрения потребностей авиации) и достоверные сведения о струк­туре и свойствах нижних слоев атмосферы — примерно до вы­соты 20 км. Резкое увеличение в последние годы высоты полета самолетов и ракетных аппаратов послужило стимулом к интен­сивному изучению строения высоких слоев атмосферы.

Методы изучения атмосферы. Систематические исследования высоких слоев атмосферы производятся в основ­ном при помощи самописцев и других автоматических приборов, поднимаемых на высоту на шарах-зондах или других аппаратах. Идея этого метода была разработана еще М. В. Ломоносовым, который в 1754 г. построил вертолет («аэродромическую машин­ку») для подъема метеорологических приборов.

Особенно плодотворным для широкого развития исследований атмосферы оказалось изобретение советским метеорологом П. А. Молчановым в 1930 г. радиозонда, поднимающегося до 30—35 км и передающего условными сигналами по радио ре­гистрируемые на высоте давление, температуру и влажность воз­духа. Для регистрации местоположения радиозондов применя­лась радиопеленгация, а впоследствии — радиолокация. В по­следние годы применяется подъем приборов на ракетах.

В 1934 г. были произведены ценные исследования атмосферы при рекордных полетах советских стратостатов (до* вы­соты 22 км).

Для изучения более высоких слоев атмосферы в настоящее время применяются в основном косвенные методы. Несмотря на некоторые расхождения между данными, полученными различ­ными косвенными методами, все эти методы дают сравнительно согласные результаты, позволяющие сделать основные выводы о структуре верхних слоев атмосферы.

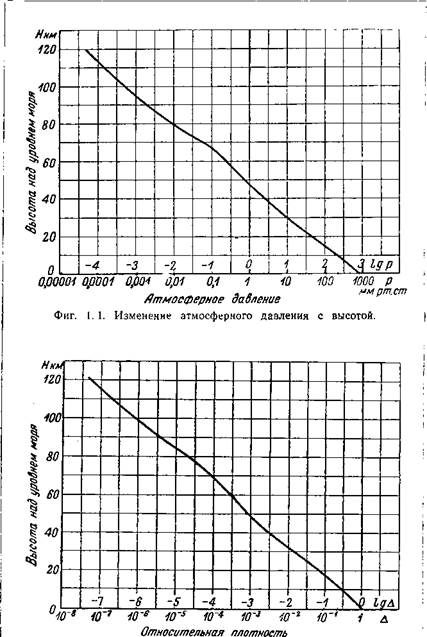
Тропосфера истратосфера. На фиг. 1.1 и 1.2 по­казан примерный характер изменения давления и относитель­ной плотности на высотах от 0 до 120 км. До 50% всей массы атмосферного воздуха находится в прилегающем к земле слое

Фиг. 1.2. Изменение относительной плотности воздуха с высотой.

высотой 5,5 км. В пределах первых 10 км находится уже около 75%, а первых 30 км — до 99% всей воздушной массы.

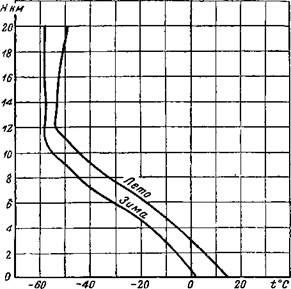
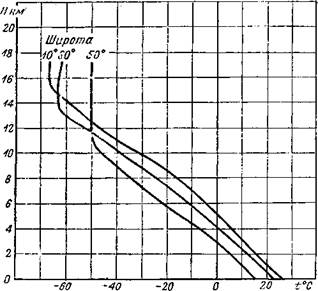
Характер изменения температуры воздуха с высотой зависит от ряда факторов: времени года и суток, широты места, условий погоды и т. п. На фиг. 1.3 приведено типичное вертикальное распределение средних температур зимой и летом по данным шарозондовых наблюдений четырех европейских станций, распо­ложенных приблизительно на одной и той же географической широте (48° с. ш.) и имеющих более или менее аналогичный климат, а на фиг. 1.4 — примерное распределение среднегодо­вых температур воздуха в атмосфере по вертикали для трех географических широт: 10°, 30° и 50^.

На фиг. 1.3 и 1.4 видно, что для средних широт на высотах до 11 км температура воздуха убывает с высотой примерно на 6—7° на 1 км; в интервале высот от 11 до 20 км температура остается почти постоянной и равна от —50 до —60° С.

Нижний слой атмосферы, в котором наблюдается значитель­ное убывание температуры с высотой, называется тропосфе­рой. Для тропосферы характерно интенсивное перемеши­вание слоев воздуха как в горизонтальном, так и в верти­кальном направлении. В тропосфере часто образуются верти­кальные течения масс воздуха, приводящие к кон­денсации водяных паров, образованию облаков и туманов и вы­падению осадков. В тропосфере дуют переменные по силе и направлению ветры и происходят непрерывные изменения температуры, давления, влажности и других фи­зических параметров воздуха. Происходящие в тропосфере про­цессы оказывают решающее влияние на условия погоды.

Расположенная над тропосферой область атмосферы с почти постоянной по высоте температурой называется стратосфе­рой или изотермической областью. Переходный слой высотой до 2 км, отделяющий тропосферу от стратосферы, на­зывают тропопаузой или субстратосферой. В этом слое характерные для тропосферы процессы вертикального пере­мешивания воздуха постепенно убывают, в самой же стратосфере почти нет вертикального перемешивания слоев воздуха. Вслед­ствие ничтожного количества водяных паров в стратосфере не бывает облачности и туманов. Направление ветров почти по­стоянно.

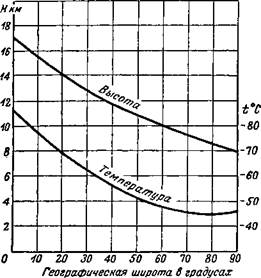
Высота нижней границы стратосферы зависит от географи­ческой широты места, времени года и от характера погоды. На фиг. 1.5 показана средняя зависимость высоты нижней границы стратосферы (тропопаузы) и температуры воздуха в ней от ши­роты места. Среднегодовая высота тропопаузы повышается от 8 км на полюсах до 17 км на экваторе, а на широте 45° она равна 11 км. Среднегодовая температура в стратосфере убывает от—45° С на полюсе до—85° на экваторе. Высота тропопаузы понижается весной и повышается осенью. Тропопауза располо-

Фиг. 1.3. Типичное вертикальное распределение температуры воздуха зимой и летом на широте 48°.

Фиг. 1.4. Примерное вертикальное распределение среднегодовых температур на широтах 10э, 30° и 50°.

жена выше над областями с высоким атмосферным давлением при антициклоне и ниже над областями с низким давлением, т. е. при циклоне. В первом случае температура в стратосфере ниже* чем во втором, на 5—10° С.

В настоящее время нет единой общепринятой терминологии в отношении высоких слоев атмосферы. Некоторые авторы счи­тают верхней границей стратосферы высоту в 20 км, а слои, ле­жащие выше нее, называют «высокими слоями» атмосферы. Дру — гие’считают верхней границей стратосферы высоту в 80—100 км, выше которой лежит так называемая ионосфера.

Фиг. 1.5. Зависимость высоты тропопаузы и среднегодовой температуры в стратосфере от географической широты.

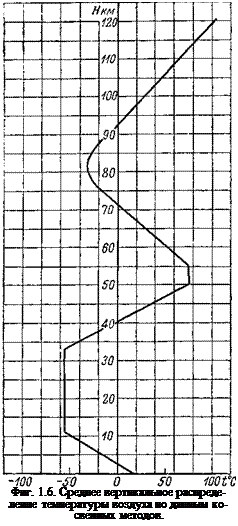
Высокие слои атмосферы. Имеющиеся в настоящее время различные данные о вертикальном распределении темпе­ратуры до высоты 100 км показывают, что постоянство с высотой температуры в стратосфере наблюдается только до высоты по­рядка 35 км. С этой высоты начинается значительное увеличение температуры, которая достигает максимального значения около — г-75° С на высоте 50—55 км. После этого температура вновь начинает понижаться и достигает—30° С на высоте 80 км. С этой высоты температура вновь начинает непрерывно возрастать,, достигая величины +100° С на высоте 120 км. На фиг. 1.6 при­водится среднее распределение температур по высотам по дан — ным косвенных методов.

Данные о распределении температуры до высот порядка 100 км, полученные различными косвенными методами, более или менее близки.

Следует иметь в виду, что в верхних слоях атмосферы вслед­ствие большой разреженности воздуха теплопередача от воздуха

к телу протекает настоль­ко медленно, что большая часть сообщаемого телу тепла рассеивается излу­чением. Таким образом для больших высот нель­зя отождествлять температуру тела с температурой окру­жающей среды, что допустимо в земных усло­виях. Вследствие соб­ственного излучения тела на больших высотах тем­пература тела будет не­сравненно ниже, чем тем­пература окружающего тело воздуха.

Значительные колеба­ния температуры воздуха на больших высотах в за­висимости от времени су­ток и факт наличия весьма высоких температур на этих высотах становятся понятными, если учесть, что вследствие большой разреженности воздуха внутренняя энергия и теп­лосодержание воздуха ничтожны по сравнению с земными условиями. Вследствие этого ничтож­ное изменение сообщае­мого воздуху тепла может привести на этих высотах к резкому изменению тем­пературы воздуха.

Колебание дав­ления и температуры. Крайние пределы изменения давления, наблюдавшиеся на уровне моря, соответствуют 685— 800 мм рт. ст. Изменения давления на уровне моря в пределах 730—780 мм можно считать обычными. Одной и той же геомет­

рической высоте соответствуют меньшие давления и большие плотности зимой по сравнению с летом. Кроме того, давление воздуха подвержено суточным периодическим колебаниям, одна­ко амплитуда этих колебаний невелика.

Годовая амплитуда температу­ры, т. е. разность между средни­ми температурами наиболее теп­лого и наиболее холодного ме­сяцев, равна в средних широтах примерно 30°, а суточная ампли­туда 4°. В Сибири разность между иаивысшей и наинизшей темпера­турой, наблюдаемой в течение го­да, доходит до 90р, соответствую­щая цифра для средних широт СССР доходит до 70° (от —35° до 4-35°). С поднятием на высоту — диапазон изменения температуры воздуха уменьшается.

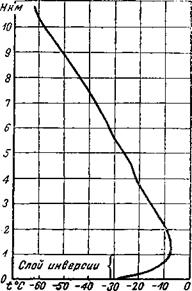
Довольно значительные изме­нения наблюдаются и в величине вертикального темпера* тур ного градиента. В не­которых случаях зимой наблю­дается так называемая и н в е р — сия температуры, заключающая­ся В ТОМ, ЧТО на малых высотах Фиг. 1.7. Пример зимней инвер — Гдо 1 км) наблюдается рост тем — сии-

пературы с высотой. На фиг. 1.7

приведен пример зимней инверсии, при кото-рой температура на высоте 1 км превышает температуру у земли больше, чем на 20:>.

§ 2. ФИЗИЧЕСКИЕ ПАРАМЕТРЫ ВОЗДУХА И ИХ ИЗМЕРЕНИЕ

Основными параметрами, характеризующими состояние воз­духа, являются давление, температура и плотность. Изменение этих параметров определяет изменение других свойств воздуха, например, скорости звука, вязкости, теплопро­водности.

Давление воздуха измеряется несколькими единицами.

Давление, равное 1 кг/см2, называется метрической (или технической) атмосферой:

1 am=l кг/см^=Ю 000 кг/м*.

В физике за одну атмосферу принимается среднее давление атмосферного воздуха на уровне моря; эта единица измерения называется физической атмосферой и обозначается 1 Ат, причем

1 Ат= 1,0332 кг/см%= 10 332 кг/м*.

2 772

Кроме этого способа измерения давления воздуха как силы, применяется, как известно, другой способ измерения, при кото­ром давление определяется высотой уравновешивающего его столба жидкости ■— воды или ртути. Высота столба жидкости h пропорциональна величине давления и обратно пропорциональна

удельному весу жидкости, т. е. h = —. Так как удельный вес

7

ртути при (PC равен 13 595 /сг/ж3, а воды — 1000 /сг/ж3, то
1 am — 1 кг/см%= 10 000 кг/м2= 10 ж вод. ст. = 735,6 мм рт. ст.,
1 Ат= 1,0332 кг/слс2=ю 332 кг/м*= 10,332 м вод. ст. =

= 760 мм рт. ст.

Таким образом переход от давления, измеренного в мм рт. ст., к давлению, измеренному в метрических атмосферах, следует производить по формуле

, 9 р мм рт. ст.

р кг см2 = —————— .

г 1 735,6

При измерениях давления часто определяют избыток действи­тельного давления р над атмосферным давлением рн

Ризб —Р pH.

Давление ризб называется избыточным или маномет­рическим давлением, а давление р — абсолютным. Так как газы не могут работать на растяжение, то абсолютное дав­ление их не может сделаться отрицательным.

Температура воздуха измеряется либо по стогра­дусной шкале (°С), либо по так называемой абсолютной шкале (° К), причем

Г=273 + /,

где Т—абсолютная температура в °К, a t — температура в °С. Таким образом величина одного градуса одинакова в обеих шкалах, но нуль абсолютной шкалы на 273° ниже нуля стогра­дусной шкалы.

Плотность воздуха характеризуется либо удельным объемом его v, либо весовой плотностью 7, либо массовой плот­ностью р. Удельным объемом воздуха v называется объем (в ж3), занимаемый 1 кг воздуха, следовательно, размерность v будет ж3//сг.

Весовой плотностью воздуха называется вес в кг 1 ж3 воздуха:

7 = — кг! м*

V

следовательно’, весовая плотность есть величина, обратная удель­ному объему.

Массовой плотностью воздуха р называется масса воздуха, находящаяся в 1 ж3 его. Массовая плотность

р = — кг сек12/лі*,

g

где g— ускорение земного тяготения, равное для средних широт 9,81 м/сек[1] [2].

В широком диапазоне изменения температур и давлений воздуха можно пользоваться так называемым уравнением состояния газа:

(1.1)

где R — газовая постоянная. Для обычного состава воздуха в тропосфере /?=29,27 кем/кг град.

Заменив в уравнении состояния 7 величиной pg, получим часто применяемую формулу для вычисления массовой плот­ности о по давлению р (в кг/м2) и абсолютной температуре Т воздуха

Введя вместо р в кг/м2 его значение в мм рт. ст. и подставив вместо g и R их численные значения, получим следующие фор­мулы:

: 0,4645

о = 0,04737 ,

где р — в мм рт. ст.

При так называемых нормальных условиях т. е. при р0=- =760 мм рт. ст. и /о^іб0 С, величина массовой плотности р0 равна Vs’

р о== Vs=0,125.

Отношение массовой плотности воздуха в действительных условиях о к массовой плотности при нормальных условиях р0 называется относительной плотностью воздуха и обозначается через Д:

Д = — Р-.

Ро

Подставляя вместо р и р0 их значения, получим часто при­меняемую при обработке результатов летных испытаний фор­мулу

где р берется в мм рт. ст.

Вязкость воздуха. Для характеристики сил внутрен­него трения в воздухе, иначе называемых силами вязкости, при­меняется так называемый динамический коэффициент вязкости или кинематический коэффициент вязкости v, равный отношению динамического коэффициента вязкости к плотности:

Сила трения dX, действующая на какой-либо элемент площади dS, равна

dX = |х — dS,

dy

dV

где -— —градиент скорости воздуха по нормали к поверх­ности элемента dS. По формуле для dX можно найти размер­ность коэффициента вязкости »>.

_ кг]м] _	‘кг-сек
	’ м сек	[м*]	м*

а по формуле (1.5)—размерность кинематического коэффици­ента вязкости

Как показывает кинетическая теория газов, коэффициент вязкости ч не зависит от давления и плотности газа, а только от его температуры. При ^=0°С коэффициент вязкости для воз­духа ч0= 1,712 • 10~6 кг сек/м?. Для других температур коэффи­циент вязкости воздуха может быть определен ПО’ формуле

= + 0,003665+0 + 0,00080% Го	(1.6)
или по следующим приближенным формулам:
!А / Г °Д6	(1-60
Но /о /
— = 1 + 0,00278£,	(1.6′)
НО

дающим хорошие результаты в пределах изменения температур от —50° до +50° С. В формуле (1.6′) 7,0 = 273°К.

Как видно из приведенных формул, с повышением темпера­туры коэффициент вязкости несколько увеличивается.

Кинематический коэффициент вязкости зависит как от тем­пературы, так и от давления воздуха. При нормальных условиях (рд = 760 мм рт. ст. и /0=15° С) кинематический коэффициент вязкости v = 14,41 • 10~6 м2/сєк.

Скорость звука. Из акустики известно, что скорость звука, т. е. скорость распространения в газе малых возмущений, при адиабатическом процессе распространения звука равна

где k— ■—отношение удельных теплоемкостей при тюстоян-

cv

ком давлении и постоянном объеме. Для воздуха k равно в среднем 1,4.

Подставляя вместо — его значение по-уравнению состояния р

(1. Г), получим, что скорость звука равна

а = У kgHT, (1. Т)

или для воздуха

а = 20,05 У Т М/!сек = 72,2/Т км/час; (1.7")

следовательно, скорость звука пропорциональна квадратному корню из абсолютной темпера­туры. При /=15° С скорость звука а = 340,2 м/сек.

Влажность воздуха оказывает влияние на его плот­ность, причем влажный воздух всегда легче сухото при одинако­вых давлении и температуре. Оценим это влияние количественно.

Абсолютной влажностью называется количество водяного пара в единице объема воздуха; обычно она измеряется в г/мк Как известно из термодинамики, смеси газон подчиняются закону парциальных давлений: давление смеси равняется сумме парци­альных давлений отдельных газов, входящих в смесь. Если обо­значить парциальное давление (упругость) водяных паров через рп, а парциальное давление сухого воздуха через рв, то абсолют­ное давление влажного воздуха будет равно

р—Рв + Рп.

Для рассматриваемого диапазона температур для пара мож­но пользоваться уравнением состояния в том же виде, что и для газов

„ „ Рп

ІП ГІ т 9

где я„=47,1 —газовая постоянная, а и рп—-плотность и давление водяного пара. Таким образом при постоянной темпе­

ратуре Т плотность водяного пара уп пропорциональна его упругости рп.

Как известно’, для каждой температуры имеется предельное — значение количества водяного пара, которое может содержаться в воздухе и соответствует состоянию насыщения объема про­странства водяным паром. Соответствующие состоянию на­сыщения давление и плотность водяного пара называются дав­лением рн. п и плотностью ун. п насыщенного водяного пара. В табл. 1 приведены значения давления и весовой плот­ности насыщенного водяного пара в зависимости от темпера­туры.

Таблица 1

Давление и плотность насыщенного водяного пара О О Рн. п ММ рт. СТ. і 7н. п 2’М^ — 20 0,960 1,00 — 10 2,159 2,22 0 *4,579 4,74 -f 10 9,21 9,4 + 15 12,79 12,83 4- 20 17,5 17,3 4 30 31,8 30,4 4- 40 55,3 51,2 4 50 92,5 83,2

Относительной влажностью х называется отно­шение количества водяного пара, находящегося в воздухе, к ко­личеству водяного пара, насыщающего пространство при той же температуре

__ 7п

— •

^н. п

Воспользовавшись уравнением состояния для водяного пара, найдем что

X — Ь == р п

‘ н. II Р и. п

ИЛИ

Рп = ХР*- П-

Таким образом, зная относительную влажность х и найдя при помощи табл. 1 рн. п, по температуре воздуха можно определить парциальное давление водяного пара рп. Относительную влаж­ность часто указывают в процентах.

Выведем формулу для определения плотности влажного воз­духа у по заданным относительной влажности х, давлению воз-‘ духа р и температуре Т. Плотность влажного воздуха *у равна сумме плотности сухого воздуха 7в и водяного пара Yn-

ї = Тв+ їп-

Воспользовавшись уравнениями состояния для сухого воздуха и для водяного пара, получим что

Рв_ , RT^Rn

По закону парциальных давлений

р = рв + рп,

следовательно,

р, ъ — р — Рп-

Так как рП = хрнп, то

Л _ Р-ХРн. п ХРу. п L *Л,. п Л __JL

[ RT + RnT RTL р V RJ.’

Подставив вместо R и Rn их значения 29, 27 и 47, 1, получим

ї = ~ (l-0,378^). (1.8)

Из формулы (1.8) видно, что плотность влажного воздуха всегда меньше плотности сухого воздуха при одинаковых давлении и температуре. Однако даже при относительной влажности х=1 (т. е. 100%) поправка на влажность при определении плотности невелика. Так, для нормальных условий на уровне моря при х= получим поправку

хр„ _ Ы2,79

0, 378————— = 0,378 = 0,00635,

р 760

т. е. меньше 0,7°/о. Для средних условий на высоте Н=5000 м эта поправка равна 0,00117, т. е. меньше 0,2%. На еще больших высотах она исчезающе мала.

Поэтому при летных испытаниях обычно не определяют от­носительной влажности воздуха и подсчитывают плотность по формулам для сухого воздуха. Однако в случае очень высоких температур воздуха и большой влажности, встречаемых иногда

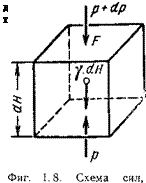
Если известен закон изменения темпера­туры в зависимости от высоты Я или дав­ления р, то, проинтегрировав уравнение (1. 10), мы найдем связь между давлением и высотой, а затем по уравнению (1.1′) — связь между плотностью и давлением или высотой.

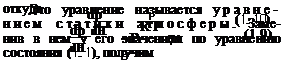Определение геометрической высоты

В результате обработки материалов испытательного полета обычж> может быть построена зависимость абсолютной темпе­ратуры Т от атмосферного давления р: T=f(p). Зная эту зави­симость, можно — определить абсолютную (геометрическую) вы­соту полета Я. Для этого в уравнение (1. 10) подставим T=f(p):

dp _ _ р dH Rf (р) 9

Интегрируя в пределах от р0 до р и от 0 до Н, найдем

Построив график изменения подинтегральной функции ——- = —

Р Р

в зависимости от р, путем графического интегрирования найдем величину интеграла, а следовательно, и величину Я для разных значений р.