СИСТЕМ ТЕЛЕУПРАВЛЕНИЯ

5.1. ОЦЕНКА ВОЗМОЖНОСТЕЙ ПРОТИВОДЕЙСТВИЯ

В СТАЦИОНАРНОЙ СИСТЕМЕ НАВЕДЕНИЯ

Как рассматривалось в гл. 1, цель располагает двумя возможностями воздействия на систему наведения: из­менением динамических характеристик собственного движения (маневра) и созданием помех, искажающих полезную информацию [22].

Воздействие на систему управления маневра цели мо­жет быть учтено, если рассматривать уравнения объекта управления в виде

^=Ax—Buu—Bvv—, x(t0)—xQ. (5.1)

at

Управление цели г» является в общем случае вектором (mX 1), удовлетворяющим условиям (гл. I)

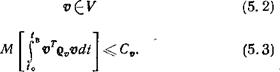и

Предположим, что цель располагает лишь априорной информацией о характеристиках системы наведения. В этом случае v(t) не зависит от реализации случайных воздействий на систему наведения и может рассматри­ваться как неслучайная функция времени. При этом огра­ничение (5.3) примет вид

(5.4)

Рассматривая линейные задачи, предположим также, что действие помех, создаваемых целью, сводится к изме­нению ошибок n(t) в измеряемом наводящимся объек­том векторе г(ІХ 1):

z=Cx(t)-{-n(t). (5.5)

Если цель и в данном случае действует только на ос­нове априорной информации, она выбирает статистиче-

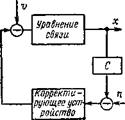Рис. 5.1. Структурная схема системы наведения

ские характеристики n(t). При этом ограничена диспер­сия (мощность) создаваемой целью помехи

M[nT{t)n{t)]<Dm. (5.6)

В стационарном случае условие (5.6) может быть представлено через спектральную плотность n(t), рав­ную sn(iо), в виде

jS„(<o)rf«> <£>m. (5.7)

Предположим, что цель выбором помехи n(t) и уп­равления ©стремится максимизировать

I=M [JitJPxV,)] (5.8)

при условии, что эти функции удовлетворяют ограниче­ниям (5.6), (5.2) и (5.3). Объект (5.1) и систему наве­дения будем предполагать стационарными, g(Y}=0.

Структурная схема системы приведена на рис. 5.1. Обозначим через Qn(t — т) матрицу импульсных пере­ходных функций замкнутой системы (рис. 5.1) от входа n(t) до x(t), а через Q„(t — т) —от входа© (t) до x(t).

Тогда

U

■*(*■)=J Qv(tB—x)Bvv(x)dx +

* t0

+ J Qn(tв — x)n(x)dx—Qv{tB—t0)x(tQ). (5.9)

Управление v(t) предполагается неслучайным, a n(t) не коррелировано с. начальными условиями. Подстав­ляя (5.9) в (5.8), получим, что I состоит из 3 слагае­мых, одно из которых зависит только от v(t), второе от n(t), а третье определяется х0 и не зависит от цели.

Таким образом,

	(5.10)
	(5.11)
«В •^v(/b)==:j Qv(tв x)Bvv(x)dx9	(5.12)
f0 *,-*• *B-*o J dx f dlQn(x) Rn(tB — T, tB — X)Ql(X); b о	(5.13)
Rn(tly t2)=M [«(/x) яГ (*,)];	(5.14)
(4 к) DxoQv {tB ^o)>	(5.15)
DXo = M[x(t0)xr(t0)].	(5.16)

Рассмотрим сначала задачу определения статистиче­ских характеристик помех n(t), максимизирующих (5.8). На основании (5.10) задача сводится к выбору корреля­ционной функции Rn{t, к) (5.14), максимизирующей (5.13) прд известной матрице импульсных переходных функций системы Qn (т).

Будем рассматривать для простоты одномерный слу­чай и предположим, что n(i) является стационарным процессом, a to——оо, т. е. в системе имеет место устано­вившийся процесс. В этом случае /г может быть выра­жен через передаточную функцию Qn(j(o) системы и спектральную плотность помех n(t):

/2= JJQ„ (»1*А (ш) dm. (5. 17)

Поскольку функция под интегралом является чет­ной, то

/2=2 pQ„(/a))|2S„((B)rf(B. (5.18)

о

Условие (5.6) в этом случае может быть записано в виде (5.7)

• ‘ — ?$,(«)<*«> <Ц„. (5.19)

о

Кроме того, из определения спектральной плотности, как мощности процесса следует, что

5я(м)>0. (5.20)

Применяя детерминированный принцип максимума к функционалу (5.18), получим, что максимум /2 достига­ется на 5„(<о), минимизирующей функцию Н:

min#=min—|Q„(y<o)|25„(<o). (5.21)

Поскольку I Qn (/о>) |2>0, то минимум Н при условии (5.20) достигается на границе и ограничение (5.19) со знаком равенства должно учитываться при решении за­дачи.

С учетом (5.19) задача сводится к определению 5„ (с») из условия

min Я=min—[|Q„ (jо)|* S„ (») — Н»5п(<о)], (5.22)

s„ s„

ft ft

где ф =const. Если 5п(со) не ограничена, то задача не имеет единственного решения. В частности, можно пред­положить, что максимум /2 будет достигаться при усло­вии, что

5.(»)=С8(«-®«). (5.23)

где значение сот определяется равенством

IQ» (/Ч*)!2=тах I Q„ (уш)|2. (5, 24)

О»

В этом случае помеха представляет собой гармониче­ское воздействие на частоте, соответствующей макси­мальному значению амплитудной характеристики конту­ра наведения. Фаза гармоники является случайной, а ам-

плитуда C=Dn. Для исключения 6-функций в решении можно вместо (5.19) задать ограничение в виде

(«)«/« </?„,. (5.25)

В этом случае имеем

min tf=min— [|Q„(>)|2S„-|-il>S„]. (5.26)

Sn

Дополняя (5.26) до полного квадрата, при ф<0 по­лучим

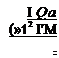
(5.27)

Подставляя (5.27) в (5.25), получим

В этом случае S„(cd) совпадает по форме с ампли­тудной характеристикой системы наведения.

Рассмотрим далее случай, когда наряду с выражени­ем (5.19) ограничена величина спектральной плотности, т. е.

0<S„(«))<5raax. (5.29)

В этом случае S„ определяется из формулы (5.22) при условиях (5.29). Оптимальная величина 5„ равна.

если [|Q„(»|2-H]>0 I 0, если [|Q„(yo>)|2+^] <0,

где постоянная ф<0 определяется из условия (5.19).

В частности, если | Q« (/со) |2 монотонно убывающая функция, то существует одно значение <i) = coc, при кото­ром (5.30) меняет знак. Это значение частоты опреде­ляется из условия

откуда

Если | Qn (/со) |2 имеет максимум на частоте сот, то интервал частот Д© = (02 — соь на котором помеха отлич­на ОТ нуля, содержит £Dm И равен

(5,34)

*^max

Значения ©і и ©2 определяются как точки пересече­ния прямой, параллельной оси абсцисс, с графиком | Qn (/©) 12> отстоящие друг от друга на величину Дш.

Таким образом,’с учетом ограничений формул (5.29) и (5.19) спектральная плотность помехи равна макси­мальной величине на интервале частот наибольшего уси­ления контура наведения, длина которого определяется условием (5.19).

Рассмотрим теперь задачу определения маневра це­ли v(t) максимизирующего выражение (5.8) при огра­ничениях, заданных формулами (5.2), (5.4) и при усло­вии, что известна матрица весовых функций системы на­ведения Q„(т). На основании условия (5.10) эта задача сводится к выбору функции времени г>(0» максимизиру­ющей /і, и может быть решена при помощи детермини­рованного принципа максимума Л. С. Понтрягина.

Поскольку управление ©(£), обеспечивающее макси­мум / ь одновременно обеспечивает минимум —11, будем рассматривать условия минумума

/і = Xv (^„) РXv (/„)

при условиях (5.2) и (5.4).

Обозначим

t

Qv№в t)Bvv(x)dх.

t0

Отсюда

xv(i0)=0.

at

На основании правила множителей Лагранжа полу­чим, что минимум (5.35) достигается на управлениях, обеспечивающих максимум функции Я:

Н =<1>TQv{tB—t) Bvv (О+Фл+а^бЛ (5.38)

где ф„+2 определяется из условия (5.4), а вектор сопря­женных функций ф(пХ1) удовлетворяет системе диффе­ренциальных уравнений

^=0 dt

при конечных условиях

♦о (0=1

Ф(0=2Рдс(0.

Отсюда =const и (5.38) может быть записано в виде

H = 2xT{tB)POv{tB—t) Bvv {t)-{-^n+2vTQvv. (6.41)

Можно показать, что управление v(t), максимизирующее Н при условии (5.2) максимизирует

шах Hv=max<]>„+2 [даг xl (/„) PQv{tB—t) X

<-ек L 4я+2 J

Qv BVQV (tB і) Pxv (/B)j. (5.42)

При положительно-определенной матрице макси­мум (5.42) имеет место при ф«+2<0.

Если область V представляет собой такой т-мерный куб, что компоненты Vi независимы, максимум (5.42) до­стигается на управлениях

да (t)=-Sg &xBlQTv(tB-t) Pxv (tB), (5.43)

Фя+2

где обозначено

‘X при | < Vmax

Утк при X>V

ігах»

V’max — длина ребра куба.

Векторное уравнение (5.43) формально выражает связь между компонентами векторов слева и справа от знака равенства при Vmax=^maxi-

При отсутствии ограничения (5.4) фп+2=0 и опти­мальное управление у (^) определяется уравнением

(5.45)

169

которое понимается как равенство компонента векторов в левой и правой частях.

При отсутствии ограничения (5.2) из формулы (5.43) получаем

Рассмотрим решение уравнений (5.45) и (5.46) в одно­мерном случае (n=m= 1) при Р>0. Подставляя выра­жения (5.45) в формулы (5.12), получаем при п=т= 1, что x(tb) >0. Отсюда

«(O—V’neSign^Qj^-/). (5.47)

Следовательно, при ограничении (5.2) управление це­ли, максимизирующее квадрат ошибки, принимает зна­чения на границе допустимой области и является ре­лейным.

Для определения множителя Лагранжа qv подставим его в выражение (5.4). В одномерном случае получим, что i|}„+2<0, при котором имеет место максимум (5.42), равно

— B2vQlv(tB-t)dt

Qv

cv

(5.49)

Подставляя далее выражение (5.49) в формулу (5.12), получаем окончательно оптимальное управление цели при ограничении (5.4) в виде

_______ BVQV (tB — t) (5*50)

Qv

(tB — t) dt

В общем случае при ограничениях (5.2) и (5.4) зада­ча решается аналогично. Подставляя управление (5.43)
в одномерном случае в выражения (5.4) и (5.12), полу­чаем

v(t)=Sg —

« Qv

где Л=congt> 0 и определяется из уравнения <в

Q„[Sg^BeQv (K-t)Jdt=Cv.

to

Полученные оптимальные управления v(t) (5.47) и

(5.49) , обеспечивающие максимум среднего квадрата ошибки наведения, принимают значения на границах об­ластей, определяемых ограничениями (5.2) и (5.4), и за висят от характера этих ограничений.

5.2. ИГРОВАЯ ЗАДАЧА С НЕПОЛНОЙ ИНФОРМАЦИЕЙ

Рассмотрим задачу наведения с известным моментом встречи /в и целью, выбирающей свое управление tf(mXl) из условия максимума математического ожида­ния квадратичной формы координат объекта х

x=Ax—Buu—Bvv+, х{і0)=х0 (5.51)

в момент времени /в- Управление и наводящегося объек­та, как и ранее, минимизирует

I=M[xT(tJP(tJx(Q]. (5.52)

Предположим, что и VI v используют для управления вектора zu{t (/XI) и zv{t), {kX 1)

*.(*)=Ce*(/)+».(*).

(5.53)

(*) + «„ (9,

т. е.

«=»(**>, t), (5.54)

v = v{zUt), (5.55)

где, как и ранее, z*0 — совокупность значений вектора

z(t),

Предположим, как и в гл. III, что и и v удовлетворя­ют условиям

Г ‘в т

М J UTQuUC

Jo

Г

М f VTQ„V

Рассматриваемая игра двух лиц является игрой с не­полной информацией, поскольку управления и и v явля­ются операторами только ги и zVi а не координат х объекта.

Будем искать решение этой задачи в чистых стратеги­ях и предполагать, что правило множителей Лагранжа выполняется.

Таким образом, определение оптимального поведения и и V сводится к нахождению экстремумов функционала согласно 2.5:

‘в

l=xT *TQ„vdt+

to

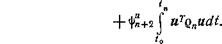(5.58)

Согласно выражениям (2.157) и (2.158) необходимым условием экстремума (5. 58) являются условия

тахМ{Н(х, и, v0, ^|^bo}=0, (5.59а)

U

ч

vcinM {Н {х, и0, V, /) | ^Іо>=0, (5.596)

V

где и0 и v0 — оптимальные законы управления. Для функционала (5.58)

Н(х, ф, и, гО=Фг 1] —

— fn+2VTQvV — ^an+2UTQ„U— фя+1. (5. 60)

Вектор-функция ф(^) удовлетворяет уравнению

— Атъ (*), Ф (*.)= -2Px(tB). (5.61)

Отсюда

ф(/)=_2*г(/в, t)Px(tB). (5.62)

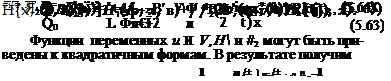Отметим, что из выражения (5.60) функция Н пред­ставляется в виде

Я3 (Ф. •*) = ФT Ax —— ^TBttQa ‘ВІф — f

44’“+2

H——фВлТ’ЁЯ. (5.66)

*TC+2

При получении формул (5.64) и (5.65) было исполь­зовано выражение (5.62). Предполагалось, что qu и q„— положительно-определенные матрицы, а Р — симметрич­ная положительная матрица.

Из выражений (5.63) — (5.66) следует, что управле­ния обеспечивают экстремумы Я, как функции и и V не­зависимо.

Согласно (5.596) минимум МН, как функции до­стигается внутри области определения v при ф®+2 <0 для

t)P{ta)M[x{tB)zU (5.67)

Кл + 2 I

Заметим, что, как и ранее, v{t) предполагается опера­тором от zio и в выражении (5.5Э6) является неслучай­ной функцией, поскольку zio задано.

Аналогично из выражения (5.59а) максимум МН, как функции и, достигается внутри области определения при Фл+2>0 и имеет место при

»(0=

Тогда

Рассмотрим сначала случай, когда наводящийся объект и цель используют для управления один и тот же вектор измерений, т. е.

*.(*)=*,(*)=*(*)’ (5.73)

для всех t.

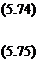Предположим, что существуют обратные матрицы (j-i и у-1. Тогда, сравнивая управления (5.67) и (5.68), находим

Таким образом, в рассматриваемой задаче несиммет — рия управлений определяется условиями (5.56) и (5.57), а также различием связи фазовых координат объекта с управлениями.

Определим оптимальные управления в рассматривае­мой задаче.

Применяя к уравнениям (5.67) и (5.68) операторы условных математических ожиданий, получим

М[и (і)| zl] =U{t)U-1 (т) и (т); (5. 76)

M[v{t)zl=iV(t)V-‘{%)v{x), ^>т. (5.77)

Свойства оптимальных управлений противников, опи­санные формулами (5.74) — (5.77), позволяют решить уравнения (5.67) и (5.68).

Согласно уравнению (5.51)

‘в

x(tB)=k{tB, + J *(*., т)[Д. я + Д„« + Є]</т. (5.78)

t

Отсюда

»W=P(*){*(*., k[tB, x)BvV{x)dx-f-

+ j * (*., t) BaU (t) dx j K-1 (t) v (oj. (5. 79)

Здесь учтено, что при

М, [и (т)] =U( т) V-1 (*) v (t). (5.80)

Если существует матрица gZ1^, обратная матрице

<в

gv{t, O = £-K(0j *(/в, т)[ДГ(*)+

t

+BuU(r)drV-1(tl (5.81)

то

v{i)=gVt, tB)V{t)k{tB, t)M[x(t)z‘o]. (5.82)

Аналогично

*{t)=gZ’V. QU{t)k{tB, f)M[x(t)z‘o], (5.83)

‘в

ГДЄ g„(f, t.)=E-U(t)$ k(tB, т)[Д„Г(т)+

t

+BuU(x)]~dTU-1(t). (5.84)

Условное математическое ожидание текущих коорди­нат объекта Mt[x(t)=x{t) определяется в рассматривае­мом случае аналогично 3.2:

4г = Ах W+Вии + Bvv + PtrTN~’ [z {t)~ Cx (0]•

(5.85) 175

В этом уравнении для управления (5.82)

u{t)=U(t)V~'{t)v{t), (5.86)

а для управления (5.83) согласно равенству (5.74)

(5.87)

Физический смысл полученного решения состоит в том, что цель создает в системе наведения обратную связь, противоположную по знаку обратной связи наводящего­ся объекта. Коэффициент этой связи определяется энер­гетическими возможностями цели, обусловливаемыми ограничением (5.57).

Если задача симметрична, т. е.

BU=BV, Qa=Qv, CU=CV, v=—u (5.88)

управление наводящегося объекта полностью скомпенси­ровано. Цена игры в этом случае определяется матема­тическим ожиданием и дисперсией выходных координат неуправляемого объекта

х=Ах-{-1, x(t0)—x0. (5.89)

Тогда

М [xT(tK)Px{Q] = SP[P(tB)Dx(tn% (5.90)

где SP — означает след матрицы, заключенной в скобки. Dx(t) удовлетворяет уравнению:

rlI±!fL = ADx(t)+Dx(t)AT+S(t (5.91)

at

где

(5.92)

Уравнение (5.91) решается при начальном условии, которое определяется априорной дисперсией начальных значений координат

Dx{Q=M[x, x J]. (5.93)

Рассмотрим теперь общий случай, когда zu(i) не сов­падает, z x{t).

В этом случае аналогично выражениям (5.76) и (5.77) Mut[u(x)) = U(T)U-‘(t)u(t); (5.94)

^/[«»(t)]=^(t)K-4<)w(0, (5.95)

где Mut и Mvt — условные математические ожидания при заданных реализациях Zat0 и zlt0 соответственно.

Для установления соотношений между управлениями и я V, аналогичных условию (5.74), предположим, что множество измерений Zut0 содержит множество гы„. Тогда

Mvt Мтх(О] = Mvtx (О, (5.96)

t <т.

Отсюда следует

Mvt% (т)=U (т)К-і (t) v (/). (5. 97)

Подставляя далее выражение (5.78) в (5.71) с учетом равенства (5.95) и (5.97), получим

*

*(*». rf)Mvix(t)+§ k(iB, x)[BuU (т)+

‘ +BvV{x)}dxV~'{t)v{t)}. (5.98)

Это уравнение аналогично (5.79) и

«С0=вгГ1(/. iB)Vt)k{tB, t)Mvix{t), (5.99)

XJIfigv(t, ^в) определяется формулой (5.81). С другой сто­роны, подставляя выражение (5.78) в (5.72) и учитывая равенство (5.94), получим

f

* n{t)=U{t)h{tB, f)Mutx00+ J *(*.. т)Х

X [ Вии (т) u-‘ (*) и (*)+ BvMtttv (т)] dx. (5. 100)

Предположим для упрощения задачи, что дополни­тельная информация наводящегося объекта, содержащая­ся в Zat0, не позволяет осуществить более точный про­гноз управления цели, чем это может осуществить сама цель на основе информации z£<0, т. е.

Л*Ит)|*і/.]=ЖИтЯ>£<#], x>i. (5.101)

Тогда согласно (5.95) при

Mat[v(x)]=Mvt[v(v)] = V (t)v (і). (5. 102)

Решая (5.100), получим

u(t)=gu(t, tB)U(t)[k(tB, t)Matx(t)— ‘в

+ j к (/B, t) BvV (t) dxV-1 (t) v (01, (5.103)

t

где

*в

Гіu{t, Q=E-U(t)J k(tB, x)U(T)dt’J-‘(t). (5.104)

t

Отметим, что в данном случае наводящийся объект, наряду с задачей минимизации ошибки наведения, на ос­нове имеющейся у него информации компенсирует дей­ствия цели (второе слагаемое в выражении (5.103)), со­здающей аналогично предыдущему случаю положитель­ную обратную связь в контуре наведения с помощью управления (5.99).

Можно показать, используя приемы, аналогичные получению оценки х (см. 3.2).

= Axv (t) + [Bv + BJJV-‘ ]«(*) +

+#*/С£ЛГГ1[*в< —xv(i0) = Mx0. (5.105) Здесь Zvt определяется выражением (5.53),

xv{t)=Mvtx{t). (5.106)

Аналогично

J^L = А*» (і) + В „и(і) + В W +

at

+. R»,ClNaX [zttt — Caxa (/)] (5. 107)

при обозначениях, соответствующих (5.53) и (5.106).

Таким образом, наводящийся объект в рассматривае­мом случае управляется так же, как при известных ап­риори статистических характеристиках движения цели и

полностью известном управлении цели в прошлом. Это естественно, поскольку вектор измерений цели является составной частью. вектора измерений наводящегося, объекта.

Случай, когда множество zlto включает в себя множество 2ut0 при выполнении условия (5.101), может быть рассмотрен аналогично. Очевидно, в этом случае цель осуществляет процесс противодействия на основе известного точно прошлого поведения наводящегося объекта. При этом оптимальным поведением цели является обеспечение максимума (5.52) при измеряемом воздействии u{i) с известными статистическими характе­ристиками.

В заключение рассмотрим вариант игровой задачи когда множества zit0 и z*vt0 не пересекаются. При этом условные законы распределения

p(zltJztt0)=p(zlio)

p(zxviJZut0)=p{zlio)

сводятся к безусловным законам.

В этом случае оптимальные управления определяют­ся уравнениями (5.71) и (5.72).

На основании условий (5.108) имеем

Mui{Mvx[x(tB)]}=Mx{tB V

Mvt {M^[x{ta))} = Mx{tB і ЮУ)

где М — знак априорного математического ожидания, t и т принадлежат интервалу управления (t0, tD). Предположим, что

ЛП*Ю1=0, (5.110)

поскольку обычно в уравнении (5.51)

M[x{t0)= 0. (5.111)

Предположения (5.108) по существу исключают воз­можность определения действий противника по наблю­даемым процессам zUi и zvt.

Действительно, на основании условий (5.109) и (5.110)

Mat[v(x)]=Mvt[u(x)]=0. (5.112)

Очевидно, свойства (5.94) и (5.95) оптимальных управ­лений сохраняются.

Подставляя (5.78) в (5.71), получаем в рассматривае­мом случае

*т

v[t)=V(t)[k{t„ t)Mvtx(t)+ J k(tB, T)BvV(x)dxX

t

хк-ЧО^ОЬ (5.ПЗ)

Отсюда

v(t)=g7htB, t)V{t)k{tB, (5.114)

где

‘в

gvl(tB, t)=E-V{t) j k(ta, T) PvV(x)dxV-1 (t). (5.115)

Аналогично оптимальное управление наводящимся объектом u(t) определяется выражением

«(0=^ (/„ t)U{t)k{t„ t)Muix{t)- (5. 116)

Матрица gu{tB, t) определяется из условия (5.104).

В рассматриваемом варианте оптимальные управле­ния игроков совпадают с управлениями при статистиче­ски заданном поведении противников. Этот результат — следствие того, что измерения не дают информации об управлениях противников как таковых, а только о резуль­татах их влияния на координаты объекта управления.