ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКОЙ БОКОВОЙ УСТОЙЧИВОСТИ

Теория боковой динамической устойчивости самолета показы­вает, что возмущенное боковое движение складывается из трех типов возмущенного движения.

Первый тип связан с движением крена. В этом случае дви­жение является апериодическим и затухает очень быстро по за­кону , где Xi имеет очень большое отрицательное значение.

Второй тип возмущенного движения также является аперио­дическим, но, в отличие от первого, движение затухает очень сла­бо или, наоборот, медленно нарастает; этот тип движения назы­вается «спиральным движением». Убывание (или на­растание) происходит по закону ёк^ , где коэффициент затуха­ния Х2 имеет малую величину. Непосредственное определение величины Х2 в полете не удается, так как этот тип движения всегда перекрывается третьим типом движения, представляю­щим собой колебательное движение, совершающееся ло закону

где Т — период колебаний;

С — коэффициент затухания;

х0 — значение параметра при исходном установившемся дви-

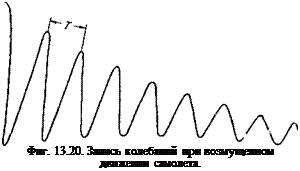
Для определения двух величин Си Т создают возмущенное движение самолета при помощи элеронов или руля направления, после чего их возвращают в прежнее положение (если опреде­ляется устойчивость с зажатым управлением) или бросают (если определяется устойчивость с брошенным управлением); при этом записывают изменение параметров возмущенного движения на ленту самописцев. В качестве параметра удобно взять любой из параметров (%і (записываются жирографом) или боковую перегрузку tiz (записывается акселерографом). Полученную запись колебательного движения обрабатывают следующим об­разом.

При умеренной степени затухания (а только такие виды движения и удается записать) можно считать, что максималь­ные и минимальные значения получаются в моменты времени т з г г

т = 0, — , Т, — и т. д. Иначе говоря, можно считать, что

2 2

пики кривой даются уравнением (п—любое целое число)

Период определяется непосредственно по диаграмме как раз­ность времени между двумя последовательными максимумами или минимумами. Остается определить величину С; из уравне­ния (13.38) и аналогичного уравнения

С тпТ

хт = х0 + Ле 2 (-1Г получаем путем вычитания

[

С пТ С ml

е * (_!)»_* 2 (-1Г

Взяв два других значения n + k и m + k, где k какое-нибудь целое число, получим

Г * пТ с mT 1 С kT

xn+k-xm+k = A[e 2 (-1 r~e 2 {-)me 2 (-1 )

Путем деления получим

xn+k ~ xm^rk
хп хт

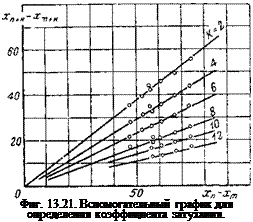
Следовательно, если при заданном k построить величины (хп+к—хт+к) в зависимости от (хп—хт) для разных значений т и п мы получим прямую линию. Угловой коэффициент этой пря-

мой даст величину е 2 . Дальше путем логарифмирования легко получить С&Г и С Г.

На фиг. 13.21 в качестве примера представлен такой график для случая записи колебательного движения, приведенного на фиг. 13. 20. Заметим, что нет нужды производить расшифровку записи; достаточно с графика фиг. 13. 20 прямо взять значения ординат от базовой линии. По графику фиг. 13.21 составляем таблицу.

k	2	4	6	8	10	12
kT «Т lk е	0,76	0,594	0,476	0,350	0,282	0,211
‘s’*	— 0,120	— 0,224	— 0,322	— 0,456	— 0,549	— 0,675
4,61 lgik ZT — * k	— 0,276	-0,258	— 0,248	— 0,263	— 0,253	— 0,259

Средняя величина £Г равна—0,26. Зная период Г=1,65 сек., получаем С=—0,158. Заметим, что величина СГ дает значение так называемого логарифмического декремента,

т. е. натурального логарифма отношения двух последовательных

2_

амплитуд. Затухание за период равно e^T = it, в нашем случае оно равно в среднем 0,769.

Часто определяют также время т2, в течение которого ам­плитуда колебаний уменьшается в два раза. Очевидно, что

В нашем случае

Характерной величиной является также отношение времени затухания наполовину т2 к периоду Т:

т2 __ 0,693

1г’~’ сг

Это отношение, как видим, обратно пропорционально логариф­мическому декременту затухания. В нашем примере — у — =2,66.

Описанный нами метод обработки вообще может служить для определения характеристик колебательного движения лю­бого типа.

При оценке боковой устойчивости очень важно также опре­делить отношение амплитуд угловых скоростей ш* и <V