ВЗЛЕТ В НЕСПОКОЙНОЙ АТМОСФЕРЕ

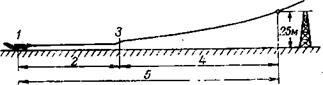
Взлетом называется процесс движения самолета от момента старта до момента достижения некоторых минимальных значе­ний высоты и скорости полета. Схема взлета показана на рис. 6.1. «Стандартное препятствие» по оси ВПП, указанное на рис. 6.1, и для взлета и для посадки считается имеющим высоту 25 м. Рассмотрим более подробно первый из двух основных этапов

Рис. 6.1. Схема взлета: I — точка старта; 2 — разбег; 3 — отрыв; 4 — разгон с подъемом; 5 — взлетная дистанция

взлета — этап разбега. Движение самолета по ВПП, по сравне­нию с его движением в воздухе, связано с рядом особенностей, основными из которых являются влияние реакций опор (колес) и изменение аэродинамических сил вследствие близости земли.

Длина разбега является очень важной характеристикой са­молета. Она зависит от многих факторов, причем некоторые из них не поддаются точному учету. К таким факторам в первую очередь относится коэффициент трения колес о ВПП, который в сильной степени зависит от погоды (осадков) и состояния по­крышек колес, а также аэродинамические силы, величина кото­рых в некоторой степени зависит от действий летчика. Поэтому длина разбега окончательно определяется в процессе летных ис­пытаний самолета. Ветер оказывает очень существенное влияние на длину разбега самолета. Так, например, для самолета Ил-28 длина разбега при встречном ветре со скоростью 10 м/сек равна 1060 м, а при попутном ветре той же скорости — 1900 м [47]. Од­нако, поскольку взлет всегда происходит против ветра, то укоро­чение разбега за счет ветра создает запас по безопасности взле*

та. Для оценки влияния ветра на время и длину разбега можно пользоваться приближенными формулами, которые получены в предположении постоянства ускорения самолета в процессе раз­бега [41]:

*рт tp[l± v0TP )•	(6.1)
	(6.2)

где /р и ip — время разбега при ветре и в безветрие соответст­венно;

£)р w и Dp — длина разбега при ветре и в безветрие соответст­венно;

Wx — постоянная составляющая ветра, совпадающая с направлением ВПП;

Vorp — скорость, при которой самолет отрывается от ВПП. В формулах (6.1) и (6.2) знак плюс в скобках соответствует попутному ветру, а знак минус — встречному. Данные о парамет­рах взлета и посадки в безветрие могут быть найдены на основа­нии анализа летных испытаний.

Значительно более важным для практики полетов оказывает­ся влияние на взлет самолета боковой составляющей ветра. До сих пор довольно значительно число случаев нарушения расписа­ния движения самолетов связано с невозможностью осуществить взлет из-за бокового ветра, скорость которого превосходит пре­дел, установленный для самолета данного типа.

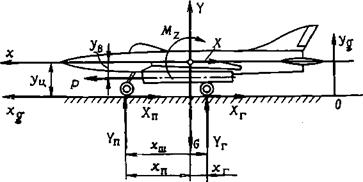
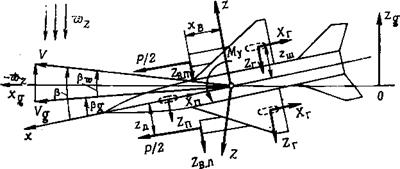
Рассмотрим уравнения, описывающие движение самолета в процессе разбега при боковом ветре. Для упрощения этих урав­нений не будем учитывать деформацию пневматиков колес и амортизаторов стоек шасси. При таком допущении движение са­молета при разбеге будет осуществляться в одной плоскости (плоскости ВПП) и, следовательно, оно будет описываться дву­мя уравнениями для проекций сил и одним уравнением моментов относительно вертикальной оси. Для анализа этих уравнений ис­пользуем земную (xg, ygt zg) и связанную (х, у, г) с самолетом системы координат. Схема сил, действующая на самолет в про­цессе разбега, а также положение координатных осей, показаны на рис. 6.2. На этом рисунке обозначено: xg, */«» zg — земные оси;

х, у, z — связанные самолетные оси;

X — сила лобового сопротивления;

Y — подъемная сила;

Z — боковая сила;

G — сила веса;

Р — сила тяги обоих двигателей;

Му, Мг — моменты относительно осей у и г;

Х„, Хг — силы трения качения переднего и главных колес; Кп, Уг — реакции переднего и главных колес;

Zn, Zr — боковые силы на переднее и главные колеса, обусловленные углом скольжения для путевой скорости;

Рис. 6.2. Силы и моменты, приложенные к самолету при разбеге с боко­вым ветром

”%.п, Хвлу— боковые силы на входе в правый и левый возду­хозаборники, обусловленные углом скольжения для воздушной скорости;

1|э — угол рыскания;

|3 — угол скольжения относительно вектора воздуш­ной скорости V;

pg — угол скольжения относительно вектора путевой скорости Vg;

Pu> — угол скольжения, создаваемый ветром.

Обозначения, относящиеся к линейным размерам, ясны из чертежа на рис. 6.2.

Движение самолета в плоскости xgOzg описывается уравне­ниями (в связанных осях):

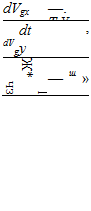
(6.3)

Кроме уравнений (6.3), описывающих движение самолета, при определении реакций колес должны использоваться очевид­ные соотношения, вытекающие из допущения о движении самоле­та в плоскости ВПП:

ЕГ=0, шх=О, ЕЛ4,=0. ,

Перейдем к рассмотрению правых частей системы уравнений (6.3). Из схемы сил на фиг. 6.2 вытекает, что

ZX=P-X cos?-*,,,, (6.5)

где Лтр — суммарная сила трения, приложенная к колесам.

Сила трения определяется соотношением

*тр = ^п + ГД (6.6)

где р — коэффициент трения качения; для бетонных полос этот

коэффициент изменяется в пределах 0,03—0,05.

Для определения силы реакций переднего и главных колес шасси (Уп+Уг) воспользуемся первым из уравнений (6.4)

rm+Yt~G-Y. (6.7)

Приближенно принимая cos 0^1 и учитывая (6.7), из (6.5) получаем окончательно

ЕЛг = /> + (рСу-С^)5-^—!хО. (6.8)

Перейдем к анализу боковых сил, действующих на самолет при разбеге. При этом предположим, что получаемые ниже урав­нения будут использоваться только для анализа движения само­лета, уже имеющего значительную скорость. Действительно, при малой скорости управление движением самолета при наличии ветра не вызывает особых затруднений, так как силы, вызывае-

мые ветром, невелики, а силы трения колес о ВПП значительны. Воздействие бокового ветра легко парируется поворотом перед­него колеса или раздельным торможением главных колес. По ме­ре увеличения скорости разбега увеличивается подъемная сила, а силы трения колес о ВПП уменьшаются. Затем переднее колесо отрывается от ВПП, и конец разбега выполняется на главных колесах (рис. 6.3). ч.

Значительная скорость движения самолета позволяет исполь­зовать приближенные кинематические соотношения

^VgJV и iws*wJV.

Рассмотрим сумму проекций сил на ось z:

£Z=Z + ZB-f-Zn + Zr, (6.9)

где Z — боковая аэродинамическая сила, вызванная

несимметрией обдува самолета;

Zb^Zb^ + Zr.., —боковые силы на входе воздухозаборников двигателей;

Zn и Zr — боковые силы, действующие на передние и главные колеса при наличии скольжения. Предположим, что для управления углом рыскания на разбе­ге используются и руль направления и поворот переднего колеса. Проведем линеаризацию выражений для боковых сил только по углу скольжения и углам отклонения переднего колеса и руля направления, выбрав за исходный невозмущенный режим прямо­линейное движение самолета. При указанных предположениях получаем следующие выражения для боковых сил.

Боковая аэродинамическая сила Z зависит от полного угла скольжения р относительно вектора воздушной скорости и от уг­ла поворота руля направления бн:

z=cls-^vg-cls-^-w2+cl«s-^zu. (6.10)

Боковая сила, действующая на входе воздухозаборников при несимметричном обтекании, равна

ZB = — kPfi = —kP$g+kPwzIV, (6.11)

ГДЄ k= WBx/(И^вых—

WBX и Wвых — скорости струи воздуха на входе и выходе двигателя соответственно.

При полете самолета обычно Z„<;Z и ZB не учитывается. При разбеге, особенно на начальном участке, роль ZB может стать значительной.

Боковые силы Zn и Zr зависят от угла скольжения рв относи­тельно вектора путевой скорости или от угла поворота переднего колеса относительно вектора путевой скорости.

Следовательно,

Z„ + Zr=Zgp, +Zn"8n + Ztyg=zl? g+Znn8„, (6.12)

где

z«—Cz к(Уп+ Гг) — 6гк(б—Y).

Таким образом,

Zn—Zr=C:UG-Y) ^+С*п/А. (6.13)

На рис. 6.4 приведен график зависимости CZK=/(pg), которая

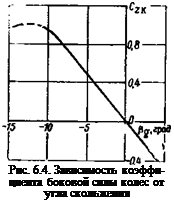определяется экспериментально. Очевидно, что коэффициент Сгк равен отношению боковой силы колеса к нормальной реакции. Из графика на рис. 6.4 следует, что при угле pg около 10° это отноше­ние близко к единице. Начиная с некоторого значения угла pg его дальнейшее увеличение приводит к уменьшению боковой силы ко­леса. Максимальное значение CZK равно коэффициенту трения скольжения для колес, движу­щихся по полосе.

На основании (6.10), (6.11) и

(6.13) получаем выражение для суммы проекций сил на ось г:

EZ=[rtS-£i + С>.(о-«’)]?,+

s ,+c;./A-(c5s-f—«w)®.- (6.14)

Рассмотрим, наконец, моменты относительно оси у, действую­щие на самолет в процессе разбега:

£Л/у=Муг—Му<ау—Мур-{-Л1у’г-{‘МуХ9 (6.15)

где Муг— момент, создаваемый боковыми силами;

МуШу— момент, обусловленный угловой скоростью щу,

Мур—момент от несимметричной тяги двигателей;

Му т— момент от несимметричного торможения главных колес;

Мух— момент относительно оси у, обусловленный момен­том относительно оси X.

На основании рис. 6.2 момент относительно оси г, создавае­мый поперечными силами, определяется выражением:

М„=ml, lS р, — mylS ■£- wt+kPxJ)t — Щ**- w, —

-С*/ЛР.+С*8.-С;.КЛ8„- (6.16)

Угловая скорость щ вызывает появление аэродинамического демпфирующего момента и дополнительного момента, обуслов­ленного изменением боковых сил всех колес из-за изменения их углов скольжения при наличии щ. Таким образом,

МуШу — М*уШу—МшуУко>у=

= —| {УуХп-^У^т) J Шу. (6.17)

Если правый двигатель дает тягу на АР большую, чем левый, то

Myp—APgj (6.18)

где 2Д — расстояние от оси двигателя до плоскости симметрии самолета.

Момент от несимметричного торможения изменяется в преде­лах от нуля до некоторого максимального значения в зависимо­сти от разности усилий, прикладываемых к правым и левым тор­мозным колодкам. Максимальное значение Myv получается, когда одно колесо полностью заторможено, а второе свободно. В этом случае

■MyTtaax — f (6.19)

где / — коэффициент трения скольжения между колесом и по­верхностью ВПП.

Момент МуХ создается при появлении момента крена. Момент крена при разбеге может появиться в результате движения со скольжением или при отклонении элеронов, т. е.

Mx=Mfyg-MlwJV+M&9. (6.20)

Момент крена положительного направления увеличивает реакцию правого главного колеса и уменьшает реакцию левого. Разность этих реакций равна

Д Уг=Мх1гш. (6.21

Неравенство реакций главных колес вызовет неравенство сил трения, в результате чего возникает момент рыскания

Ж^-рДК^ш. (6.221

Подставляя в (6.22) значение ДКГ и Мх из (6.20) и (6.21), по­лучим

Мул= %-mUS ^~wz+myS (6.23)

На основании полученных соотношений находим выражения для суммы моментов относительно оси у.

= (mils +kPXB — cl кУПХП +cl KVtxt — vmlis ^-) $g +

+ —1—^-(^nxl+Y, jc?) J <o„+

+mby4S C>/n*A- vm&S J*£-b9+APzA+

+cf^zal-(^-x9+mllS-^r +*mllS-£P)wz, (6.24)

где c — коэффициент, изменяющийся от нуля до единицы в за­висимости от степени несимметрии торможения колес. В (6.14) и (6.24) для сокращения записи не раскрыты выра­жения для реакций переднего и главных колес. На основании третьего уравнения (6.4) с учетом (6.7) и рис. 6.2 получаем:

yr -*т 4* 1Ч>Ц А1г 4* Рув

Хш Хш (6.25)

у __ у^ «*п — f*ffu | Mlг Н~ Pt/в

«*Ш

Подставляя в исходные уравнения (6.3) значения правых час­тей на основании (6.8), (6.14) и (6.24) и перенося члены с неиз­вестными функциями (параметрами движения самолета) в левые части уравнений, получаем:

206

m ^j^—{Cx-]xCy)S ■^=P—liG,

‘ ( Yп*^пН“ Yr*i

mV-^ + [kP+(CyCl«-Ct)S-^ — C^g]p*= =(-*£ ClS-£-) w,+C*S -^4 + С^КД

+ [(^-ml) IS -^ +Cl K(Vnx„ — rtxr)- kPx^ p,= = — [(w»5 + V-ml) IS j w*+rrfylS —

~ С1”кУпхвЪ„ — jx^/S-^І 8#+ДРгд + cf-lf — zm.

Уравнения (6.26) нужно дополнить формулами (6.25) и кинема­тическими соотношениями:

V=*Vgx-wx, (6.27)

^-^VgAh~^- (6-28)

Подчеркнем еще раз, что уравнения (6.26) и (6.28) могут. использоваться не с момента трогания самолета с места, а лишь с момента достижения самолетом такой скорости, при которой принятые для угла скольжения приближенные соотношения Р«,= W2/V и PsS Vgz/V выполняются с приемлемой степенью точ­ности.

Па основании пяти уравнений (6.26) — (6.28) в принципе могут быть определены пять неизвестных параметров, характеризующих движение самолета в процессе разбега: Vgx, V, pg, ф и zg. Однако для получения такого решения нужно задать скорость ветра о* как функцию времени и наложить связи на большое число пере­менных величин, входящих в правые части уравнений (6.26): Р, АР, Мг, 8н, 6П, 6Э и С.

Наиболее естественным видом этих связей являются соотно­шения, применяемые в системах автоматического управления взлетом самолета. Эти соотношения связывают указанные пере­менные величины с параметрами движения самолета. Однако, поскольку такие системы пока не получили распространения, они здесь не рассматриваются.

При использовании уравнений (6.26) — (6.28) для анализа дви­жения самолета в случае, когда управление осуществляется лет­
чиком, делаются различные допущения, сильно упрощающие задачу. Так, например, для аналитического определения времени и длины разбега можно воспользоваться первым уравнением системы (6.26), если этап разбега условно разбить на два этапа, как показано на рис. 6.3. Предполагается, что каждому из этих этапов соответствует вполне определенный угол атаки и, следо­вательно, определенные значения Сх и Су. Переход от первого этапа ко второму производится после достижения самолетом ско­рости, обеспечивающей достаточную эффективность руля высоты для управления углом атаки.

Скорость отрыва самолета определяется по формуле

(6.29)

где С„отр выбирается несколько меньше Су пред, который опреде­ляется с учетом механизации крыла и влияния близости земли.

§ 6.3. ПОСАДКА В НЕСПОКОЙНОЙ АТМОСФЕРЕ

Посадкой называется процесс движения самолета с момента выхода самолета в район аэродрома и до момента остановки са­молета в конце пробега по ВПП.

Ветер в районе аэродрома существенно усложняет все этапы посадки и его влияние увеличивается по мере приближения само­лета к земле. Продольная составляющая ветра значительно изме­няет длину пробега самолета, которая является одной из наибо­лее важных характеристик. Поскольку длина пробега при посадке обычно оказывается больше длины разбега, именно пробег опре­деляет длину ВПП. Длина пробега подсчитывается и определяет­ся экспериментально для безветренной погоды. При наличии составляющей ветра вдоль полосы посадка производится против ветра и укорочение длины пробега увеличивает безопасность посадки. По этой причине, как и при рассмотрении разбега, огра­ничимся весьма приближенной оценкой влияния продольной со­ставляющей ветра на время и длину пробега самолета. Приводи­мые ниже формулы получены в предположении постоянства замедления самолета в процессе пробега:

(6.30)

(6.29) где tn w и /п— время пробега при ветре и в безветрие соответ-

Dnw и £>п—длины пробега при ветре и в безветрие соот­ветственно;

1/пос— скорость посадки.

В формулах (6.30) и (6.31) знак плюс в скобках соответствует попутному ветру Wx, а знак минус — встречному.

Полученные в предыдущем параграфе уравнения для описа­ния процесса разбега могут быть после внесения некоторых кор — ректив использованы и для описания пробега. По этой причине ниже рассматривается специфический этап посадки — заход на посадку с момента начала снижения и до выхода самолета на высоту 30—50 м.

Наличие бокового ветра существенно осложняет процесс по­садки.

Рис. 6.5. Посадка со скольжением и с креном: а —• вид в плане, б — вид на самолет с хвоста

Для анализа динамики посадки с боковым ветром целесооб­разно рассмотреть посадку при автоматическом управлении само­летом, так как в этом случае процесс посадки поддается анали­тическому описанию.

Предварительно, однако, коротко опишем особенности посадки с боковым ветром в случае, когда самолетом управляет летчик. Боковой ветер усложняет пилотирование самолета. Как было показано в гл. 4, он вызывает снос самолета относительно вы­бранной траектории полета (см. рис. 4.1), которая в случае посадки совпадает (в горизонтальной плоскости) с осью ВПП. Парирование сноса после выхода на ось ВПП летчик может обес­печить двумя способами:

1) полетом со скольжением и с креном;

2) изменение курса полета относительно посадочного; при этом посадочным считается курс оси ВПП.

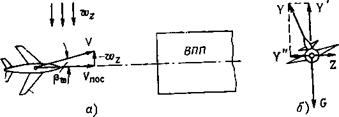
Рассмотрим первый способ. С помощью руля направления и элеронов летчик создает скольжения и крен на крыло, которое находится со стороны ветра (рис. 6.5,а и б).

Для движения без скольжения ПО ОСИ ВПП (Ря = 0) необхо­димо в соответствии с (2.22) для вектора воздушной скорости V обеспечить угол скольжения

№9=-wJV^. (6.32)

-В знаменателе формулы (6.32) указана посадочная скорость как наименьшая, при которой боковой ветер можно парировать только

Из двух предельных значений скорости бокового ветра, давае­мых формулами (6.36), нужно выбрать, естественно, меньшее. Таким образом, допустимое значение бокового ветра ограничено эффективностью рулевых органов. Обычно меньшее значение получается по второй из формул (6.36). Покажем это на следую­щем примере. Посадочный режим одного из самолетов характе­ризуется следующими данными: УПос = 70 м/сек, т? = —0,063,

т*»—- 0,137, т———— 0,069. тг« =—0,0458, битах=25°=

=0,437 рад, б9max=202=0,35 рад. Подставляя указанные значе­ния в (6.36), получаем wzi = 52 м/сек, wz2=20 м/сек.

Следует иметь в виду, что допустимое в реальных условиях значение скорости бокового ветра должно быть несколько меньше предельного, получаемого на основании (6.36). Необходимо иметь некоторый запас по углам отклонения рулевых органов, чтобы парировать порывы ветра, которые всегда сопутствуют постоян­ной составляющей ветра.

При полете со скольжением возникает боковая аэродинами­ческая сила Z, которая стремится искривить траекторию. Для обеспечения прямолинейного полета необходимо создать крен, как показано на рис. 6.5, б, чтобы парировать силу Z с помощью составляющей Y" подъемной силы. Потребный угол крена нахо­дится из первого уравнения системы (2.28) с учетом выражений для коэффициентов к? и £т, приведенных в табл. 2.2:

СІ

y==~C~V——- w*’

yev пос

Перед касанием ВПП в конце выдерживания необходимо устранить крен и осуществить приземление на оба колеса.

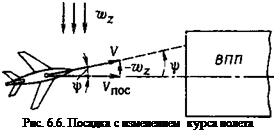При использовании второго метода парирования сноса само­лета ветром с оси ВПП изменяется курс на угол ф = а>г/УПос (рис. 6.6). При этом методе продольная ось самолета не совпа-

дает с направлением движения центра тяжести, которое проис — ходит по оси ВПП. Перед моментом приземления следует с по­мощью руля направления развернуть самолет, чтобы его продоль­ная ось совпала с осью ВПП. Это особенно важно для самолетов с хвостовым колесом, у которых главные колеса, расположенные впереди центра тяжести, создают при касании ВПП дестабилизи­рующий момент рыскания. У самолетов с носовым колесом глав­ные колеса создают стабилизирующий момент рыскания при касании ВПП, который разворачивает самолет по оси ВПП.

В процессе послепосадочного пробега самолет, обладающий путевой устойчивостью, будет разворачиваться на ветер для

устранения скольжения. Чтобы парировать разворачивающий момент, следует использовать либо несимметричное торможение главных колес, либо поворот управляемого переднего колеса.

Анализ и формулы, полученные для характеристики посадки при боковом ветре, относятся к установившемуся режиму.’ Они не показывают процесса перехода к этому режиму. Между тем неблагоприятный характер этого перехода, обусловленный не­удовлетворительными динамическими свойствами самолета, мо­жет весьма затруднить пилотирование на режиме посадки.

Рассмотрим кратко процесс захода на посадку при автомати­ческом управлении самолетом.

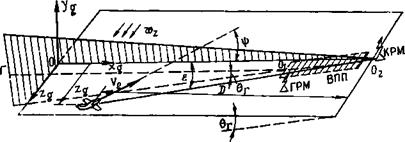
На рис. 6.7 представлена схема, возволяющая пояснить рабо­ту системы автоматического захода на посадку. С помощью кур-

Рис. 6.7. Схема посадки с использованием курсового (КРМ) и глиссадного (ГРМ) радиомаяков

сового (КРМ) и глиссадного (ГРМ) радиомаяков в вертикальной плоскости, проходящей через ось ВПП, создается глиссада пла­нирования ГО, которая имеет по отношению к горизонтальной плоскости угол наклона 6р=2°—3°. Измеряя с помощью бортовой аппаратуры нормальное и боковое отклонения самолета от глис­сады планирования и вводя соответствующие сигналы в систему автоматического управления, можно вывести самолет на высоту 30—50 м при удалении 500—1000 м от. начала ВПП. Управление самолетом от этой точки до приземления выполняет летчик.

Продольное движение самолета при посадке обычно рассмат­ривается в вертикальной плоскости, содержащей глиссаду. Наи­большее влияние ветер в районе аэродрома оказывает на боковое движение. Проанализируем боковое движение, которое будем считать происходящим в так называемой боковой плоскости, т. ё. в наклонной плоскости, перпендикулярной вертикальной, которая проходит через КРМ. Угол наклона боковой плоскости равен 0г, Т. Є. пересечение вертикальной и наклонной (боковой) плоско­стей происходит по линии ОС>2, параллельной глиссаде ГО і. Ли­ния 002 в боковой плоскости совпадает с осью ВПП и поэтому
. далее для краткости эту линию будем называть просто осью ВПП. Заметим, что в действительности боковое движение само­лета происходит не в боковой плоскости, а в параллельной ей плоскости, содержащей глиссаду ГО. Однако для упрощения кинематических соотношений удобнее рассмотреть боковое дви­жение самолета в боковой плоскости.

Для анализа бокового движения используем земную систему координат, ось xg которой направлена по линии 00$, а ось zg — горизонтальна (см. рис. 6.7). Таким образом, боковое смещение самолета относительно заданной траектории, за которуТю в боко­вом движении принимается линия 00$ — ось ВПП, равно zg. С помощью бортовой аппаратуры на самолете измеряется угол е — угол между осью ВПП и линией, соединяющей самолет и КРМ. Этот угол считается положительным, если самолет нахо­дится справа от оси ВПП. Дальность D есть проекция линии са­молет— КРМ на ось ВПП. Вследствие малости угла 8 можно считать, что дальность совпадает с расстоянием самолет — КРМ. Наконец,угол рыскания ф определяет отклонение продольной оси самолета от оси ВПП.

Рассмотрим основные соотношения, определяющие движение центра тяжести самолета в боковой плоскости. При этом для упрощения задачи будем пренебрегать временем переходных про­цессов для угловых движений самолета, считая, что они происхо­дят мгновенно. В результате этого допущения задача превра­щается из динамической в кинематическую.

В соответствии с последним уравнением системы (2.21)

(6.38)

Подчеркнем, что в уравнении (6.38) угол pg является углом скольжения для вектора путевой скорости. Поскольку автопилот управляет углом рыскания, причем предполагается, что действи­тельный угол рыскания ф мгновенно приобретает заданное систе­мой управления значение ф3, в уравнении (6.38) вместо ф введен равный ему угол ф3.

Вследствие пренебрежения временем угловых движений угол скольжения относительно воздуха р для устойчивого самолета всегда будет равен нулю. С учетом этого обстоятельства на осно­вании первого уравнения системы (2.22)

(6.39)

На основании рис. 6.7

zg=Dtgi=De.

При малом ф можно считать, что

D=D0-Vet.

Объединяя (6.38) —(6.41), получаем

(6.42)

Чтобы на основании (6.42) решать вопрос о движении центра тяжести самолета, необходимо задать какой-либо закон управ­ления углом рыскания ф3. Простейший вариант такого закона

ф3=Л. е + Д, (6.43)

где А — сумма ошибок чувствительных органов системы управ­ления.

В А входят ошибки измерителей углов ф и е. Сюда же следо­вало бы включить также ошибку гировертикали при измерении угла крена, который необходимо обеспечить для создания угло­вой скорости dty/dt. Однако при кинематическом анализе предпо­лагается, что поворот на угол ф3 происходит мгновенно, и поэтому указанная ошибка гировертикали не может быть учтена.

Подставляя значение ф3 из (6.43) в (6.42), получаем

-£«-+(*._і).—St.

ve di ‘ ve

Вводя вместо t новую независимую переменную —— =tQ—і, из (6.44) имеем

(6-45)

Wz-Ve* *.-l

Интегрируя (6.45) и учитывая соотношение (6.40), получаем решения (wz= Wz=const):

На рис. 6.8 приведены графики zg(t), построенные на основа­нии (6.47) в предположении, что ветер Wz и сумма погрешностей А равны нулю. При их построении были выбраны следующие на­чальные условия: £>0= 10000 м, /0= 180 сек, (Ve=55,5 м/сек); гво=ЮО м. Расстояние от начала ВПП до места установки КРМ равно 3000 м. Графики на рис. 6.8 построены для различных зна­чений коэффициента kt, увеличение которого приводит к сокра­щению времени процесса выхода самолета на ось ВПП.

Сравнивая графики между собой, можно установить, что для рассматриваемой задачи значения kt = (7,5—10) являются до­статочными. Следует помнить, что для реального самолета по­ворот связан с креном, который всегда ограничивается. Увеличе­ние ks приводит к сокращению зоны линейности системы управления, к резкому накренению самолета и большим угловым скоростям dyjp/dt, что будет вызывать неприятные ощущения у пассажиров.

Оценим влияние ветра и погрешностей системы управления на точность выхода самолета на ось ВПП при тех же числовых дан­ных, по которым построены графики на рис. 6.8 для случая k, = 10. В качестве оценки примем значение z# к моменту подхода самолета к началу ВПП, т. е. при t— 126 сек. Подставляя это значение в (6.47), получаем:

“gw ■

zgi= —ЗЗЗА.

Соотношения (6.48) показывают, что при боковом ветре Wz= 10 м/сек боковое отклонение составит 60 м, а при суммарной погрешности Д=0,1 рад боковое отклонение соста­вит 33,3 м. Вследствие случайного характера обо­их факторов (И72 и Д) ука­занные отклонения могут и суммироваться. При ши­рине ВПП 60 м такие бо­ковые отклонения недо­пустимы.

Рассмотренную систе­му управления самолетом будем называть статиче­ской по отношению к бо­ковому ветру и погрешно­стям измерителей.

Для ликвидации отме­ченного недостатка стати­ческой системы автомати­ческого управления введем в закон управления углом рыскания (6.43) интеграл от сигнала по углу е. В результате этот закон приобретает вид

t t

<j)3=fcte-f qt JecW-f k, bt—q, j Asdt-f (6.49)

В выражении (6.49) раскрыты составляющие ошибок системы управления, которые будем считать случайными, но не завися­щими от времени величинами. Объединяя закон управления

d*t dP

(6.49) с кинематическим уравнением (6.42), получаем общее уравнение рассматриваемой системы при интегральном управ­лении

Вид уравнения (6.50) показывает, что при интегральном управлении постоянная составляющая ветра, а также погреш­ность курсовой системы не влияет на точность выхода самолета на ось ВПП, т. е. система с интегральным управлением является астатической по отношению к указанным воздействиям. Ошибка появляется только вследствие погрешности Ае при измерении угла е. Эта ошибка очень невелика, так что практически уравне­ние (6.50) можно рассматривать как однородное. Это уравнение путем перехода к новой независимой переменной D/Ve=

= <7« (to — і) приводится к виду

(6.51)

а& aii

V

Наконец, подстановкой х, где x—f(2V^ уравне­

ние (6.51) приводится к уравнению Бесселя порядка v:

где

ї=2У?=2Vgt(t0-t), v=&,— 1.

Решение уравнения (6.52) при начальных условиях е(0)=ео,

I ) =0 имеет вид

I dt ]t=o

»«- і

е=е0р^) 2 [Л, Л, (х) —Л2У, (X)]. (6.53)

Учитывая (6.40), для бокового отклонения получаем

-і

2 [A. J.OO-iW*)!. (6.54)

В выражениях (6.53) и (6.54) J, и V, — функции Бесселя пер­вого и второго рода порядка v=kt —1 (v — целое число); посто­янные А и А2 определяются формулами;

_______ КЫ________

j,(^o)y;(x0)-j; (x0)yv(x0) jy ы

l, Ы v: (x0) — j; (x0) Ys (x0)

Jv (^o)— Jy—1 (xo) J» (xo).

*0

Y;(x0)=Y,_1 (t0)—— — Y, (T0),

Z0

x0 = 2 У~ІЇЛй=2 Vk, D0jVe.

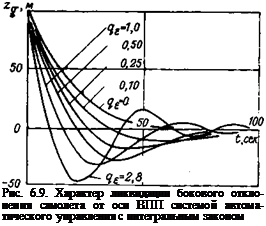На основании (6.54) построены графики zg=f(t), приведенные на рис. 6.9. При этом были приняты следующие начальные усло­вия: D0= 8900 м, /О=160 сек, (Ке=55,5 м/сек); zgo= 100 м. Значе­ние коэффициента kt было оставлено тем же, которое было вы­брано для статической системы, т. е. k, =10 (см. рис. 6.8). На рис. 6.9 указаны значения коэффициента q%, соответствующие

каждому из графиков. Сравнивая между собой кривые, которые фактически являются траекториями (так как из-за малости ф абсцисса xg = Vet), можно прийти к выводу, что наиболее плав­ная траектория получается при qt =0, и, следовательно, введе­ние интегрального управления ухудшает переходные процессы. Это действительно так, поскольку интегральное управление было введено для устранения погрешностей, возникающих за счет боко­вого ветра и ошибок измерителей, которые приводят к появлению некоторой скорости ухода самолета от оси ВПП. Поэтому, чтобы

проанализировать, например, влияние бокового ветра при инте­гральном управлении, найдем решение уравнения (6.50) при

следующих начальных условиях: е(0)=0, / —) =(—V Физи-

dt Jt= о D0)

чески такие начальные условия означают, что в момент (=0 са­молет попадает в порыв бокового ветра типа единичной функции.

Решение уравнения (6.50) при указанных выше начальных условиях имеет вид

— і

2 (6.56)

2 ie, Jv(x)—S2Y,(t)], (6.57)

В,

(6.58)

В2 =

На рис. 6.10 приведены траектории движения самолета, кото­рый на расстоянии Do = 8900 ■** от КРМ, находясь на оси ВПП, попадает в порыв ветра U7Z=10 м/сек (1^=55,5 м/сек). Значение коэффициента А, = 10. На рис. 6.10 указаны соответствующие каждой траектории значения q*t

50

Рис. 6.10. Характер движения самолета, управляемого на посадке автоматически, при воздействии ступенчатого бокового ветра

Кривые на рис. 6.10 показывают, что при q% =0 самолет к моменту /=160 сек подходит к оси ВПП с большой боковой ско­ростью, что недопустимо. При малых значениях qt максимальные боковые отклонения самолета от оси ВПП также очень велики. На основании графиков на рис. 6.10 можно утверждать, что для рассматриваемого примера наиболее подходящими значениями qt являются значения 0,5—1,0. При этих значениях qt боковое отклонение от оси ВПП и время выхода на нее являются допусти­мыми с точки зрения безопасности посадки.

Используя выбранный на основании анализа упрощенных ки­нематических уравнений закон автоматического управления само­летом при движении по равносигнальной зоне КРМ, рассмотрим полные уравнения бокового движения самолета в этом режиме. Для этой цели объединим уравнения самолета с автопилотом (2.30), уравнение закона управления (6.49) и кинематические со­отношения (6.40) и (6.41). В результате получим систему урав­нений:

—£ту——= _jL w dt ‘ pr тї dt Ve *’

«+-S — 17+V. Y-K

+(«* +/*Лн)-^ +

+/іЛнФ r==yeWz + ЛянФэ.

=^(Р,-П

/ /

|}»3=A. S-|-^, А, Де + q*j ДеЛ-f AAj),

Zg ~ De,

D=D0-W.

Для конкретного примера используем данные того же само­лета в режиме полета со скоростью Ve=55,5 м/сек, который был рассмотрен в приведенных выше примерах анализа упрощенных уравнений бокового движения. Данные о коэффициентах системы уравнений (6.59), которые используются для иллюстрации движе­ния самолета по равносигнальной зоне КРМ, сведены в табл. 6.Г.

	*т •	h		ч	1ш		П. Т	п.
0,147	0,177	5,38	6,75	2,22	—13,7	1,45	-0,256	0,43
лн	і	/. 7	Ч	Л		‘t	*«
‘—0,73	1,0	0	2.0	0.2	1.0	1.4	10	0,5

В рассматриваемом примере не учитываются погрешности чувствительных элементов системы автоматического управления, т. е. предполагается, что Дє и Дф равны нулю.

Система уравнений (6.59) с коэффициентами, указанными в табл. 6.1, была проинтегрирована на аналоговой машине при ну­левых начальных условиях применительно к случаю входа само­лета в боковой поток воздуха со скоростью Wz= 10 м/сек. Резуль­таты этого интегрирования в виде осциллограмм для наиболее

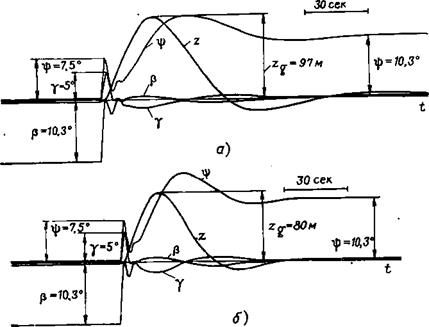
Рис. 6.11. Движение самолета в равносигнальной зоне КРМ при ступенчатом боковом ветре: а — без учета влияния изменения расстояния от самолета до КРМ; б — с учетом влия­ния этого изменения

важных параметров бокового движения представлены на рис. 6.11 и 6.12. На рис. 6.11 показано движение самолета, который встре­чает ступенчатый боковой ветер со скоростью WZ=10 м/сек на расстоянии 9000 м от начала ВПП. На рис. 6.11, а даны осцилло­граммы для случая, когда не учитывается изменение дальности до КРМ, а на рис. 6.11,6 — с учетом изменения дальности.

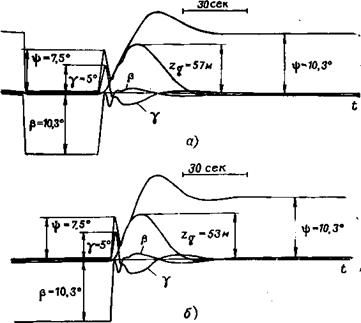
Рис. 6.12. Движение самолета в равносигнальной зоне КРМ при ступенчатом боковом ветре: а — без учета влияния изменения расстояния от самолета до КРМ; 6-е учетом влияния этого изменения

На рис. 6.12 показаны осциллограммы для этого же режима полета, но для случая, когда самолет встречает ступенчатый бо­ковой ветер со скоростью Wz= 10 м/сек на расстоянии 6000 м от КРМ или 3000 м от начала ВПП. На рис. 6.12, а приведены ос­циллограммы, характеризующие движение самолета без учета изменения дальности, на рис. 6.12,6 — с учетом этого изменения.

Момент времени, в который самолет достигает начала ВПП, на всех рисунках отмечен стрелкой, поставленной снизу оси абс­цисс.

Анализ приведенных на рис. 6.11—6.12 осциллограмм пока­зывает, что система автоматического управления боковым движе­нием самолета в режиме посадки, описываемая уравнениями

(6.58) с коэффициентами, указанными в табл. 6.1, практически

обеспечивает ликвидацию возмущения от бокового ветра типа единичной функции на расстоянии, меньшем 3000 м (рис. 6.12» кривые г8). В первые, примерно, 5 сек самолет с этой системой ведет себя так же, как и самолет с обычным автопилотом, стаби­лизирующим углы крена и рыскания (см. рис. 4.4). За это время самолет будет снесен ветром от оси ВПП, сигнал управления по углу е возрастет и начнет оказывать влияние система стабилиза­ции самолета на равносигнальной зоне КРМ. Ветер будет про­должать сносить самолет в сторону от ВПП, но с все меньшей скоростью, и через 15—20 сек с начала процесса самолет начнет возвращаться на ось ВПП. Этот процесс сопровождается плавны­ми и небольшими по амплитуде колебаниями углов крена и скольжения. В установившемся режиме все параметры бокового движения самолета (крен, боковое отклонение, скольжение) будут равны нулю. Исключение составляет угол рыскания, за счет которого и происходит компенсация начального скольжения само­лета, вызываемого боковым ветром.

В заключение этого параграфа сравним процессы движения самолета при попадании в боковой ветер, полученные на основа­нии упрощенного уравнения (6.50) и более полных уравнений

(6.59) . Решение уравнения (6.50) для рассматриваемой задачи представлено на рис. 6.10. Сравнивая график на этом рисунке, относящийся к системе, для которой <7« =0,5, с осциллограммой для zg на рис. 6.11,6, убеждаемся в том, что на основании упро­щенных уравнений (6.50) для бокового отклонения получаются результаты, весьма близкие к тем, которые дает анализ движения самолета с учетом его динамических характеристик по полным уравнениям (6.59).