О ТОЧНОСТИ СТАБИЛИЗАЦИИ САМОЛЕТА НА. ПОСАДОЧНОЙ ТРАЕКТОРИИ
Ранее при рассмотрении вопросов стабилизации самолета на посадочной траектории мы полагали, что эта траектория точно задается с помощью КРМ и КРП. Иначе говоря, мы считали отклонения курсовой линии от оси ВПП и ошибки КРП равными нулю. В действительности эти отклонения и ошибки не равны нулю и при необходмости оценить точность стабилизации самолета на посадочной траектории они должны быть учтены. Будем называть их ошибками радиотехнической траектории (ошибками радиотехнического тракта «Борт — земля») и обозначать zp.
Отклонения самолета от радиотехнической траектории являются следствием погрешностей вычислительных устройств СТУ, ошибок нерадиотехнических датчиков, неточного выполнения команд, выработанных вычислителями, турбулентных возмущений и др. Обозначим ошибки стабилизации на траектории через гс.
В таком случае боковое отклонение z самолета от посадочной траектории может быть представлено в виде суммы z=zv+zc.
Отклонения zp и zc являются результатом действия большого числа статистически независимых факторов. В первом приближении можно считать, что эти отклонения подчиняются нормальному закону распределения, что математическое ожидание отклонений близко к нулю.
Тогда плотность распределения отклонений z
![]() /(*)
/(*)
Здесь
где в ~п —среднее квадратическое отклонение радиотехнической траектории от
Г „
посадочной;
<jZc—среднее квадратическое отклонение самолета от радиотехнической траектории.
Поскольку КРМ используют угломерную систему координат, часто отклонения самолета от посадочной траектории характеризуют в угловых единицах. Иногда оказывается удобным характеризовать эти отклонения эквивалентным током КРП. В соответствии с (3.103) можно записать
где <76 — средняя квадратическая величина углового отклонения самолета от посадочной траектории;
L — дальность самолета до КРМ.
|
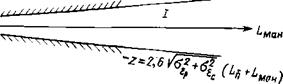
+ 2=2,6^р+Щ(^+і’**"’> |
|
С учетом (6.4) ое= — f-o*
![]() я,— средняя квадратическая величина углового отклонения радиотехнической траектории от посадочной;
я,— средняя квадратическая величина углового отклонения радиотехнической траектории от посадочной;
я, —средняя квадратическая величина углового отклонения самолета от радиотехнической траектории.
Величина а, определяется категорией КРМ и КРП. Величина зЕ(. характеризует точность стабилизации самолета на посадочной траектории и, следовательно, определяется точностью системы автоматизированного управления. Системы траєкторного управления рассчитывают таким образом, чтобы устойчивость движения обеспечивалась на некотором участке траектории после пролета высоты принятия решения. В этом случае на участке траектории протяженностью 2—3 км, охватывающем высоту принятия решения, величина Оес может быть принята примерно постоянной. Определяется величина аЕс в специальных летных испытаниях.
Дальность L зависит от расстояния Lq КРМ до базовой точки и расстояния от порога ВПП (базовой точки) до самолета. Если положить, что корректирующий маневр заканчивается в момент пролета порога ВПП, то L = L6A-LM3n.
Выше было принято, что вероятность успешных заходов на посадку должна быть рт. бок~0,988. При нормальном законе распределения отклонений ЭТО ВОЗМОЖНО, еСЛИ — При соблюдении
2(6
этого условия боковые отклонения г с вероятностью Рт. бок» 0,988 не превысят 2щах — Если известны величины Оер и CTsc, то можно определить область возможных боковых отклонений с вероятностью Рт. бок^ 0,988 в функции от LMaH (рис. 6.8). Очевидно, что эта область тем шире, чем больше величины отклонений 0£ри а , т. е. чем менее точны элементы посадочного комплекса.
При рассмотрении диапазона возможных отклонений самолета при приземлении оказывается необходимым ориентироваться на вероятности возникновения больших отклонений ~5а. В этом случае оценка ведется исходя из предположения о том, что отклонения подчиняются двойному экспоненциальному распределению. Вероятность больших отклонений (более За) для этого распределения
существенно выше, чем для нормального распределения. Оценки, полученные на основании двойного экспоненциального распределения, являются более «пессимистическими» и при решении вопросов безопасности полетов им отдается предпочтение [24].
