Сравнение результатов нескольких повторных испытаний

Сравнение результатов нескольких повторных испытаний представ­ляет собой задачу многомерного статистического анализа. Традици­онным путем решения задач данного класса является сведение мно­гомерной задачи к одномерной. При этом наиболее прост и удобен математический аппарат дисперсионного анализа.

Моделью измерений в случае различия нескольких повторных испытаний является:

ху=т0+Ъ+г9,

где Ху — у-е измерение в /-м повторном испытании (/ = 1,п); т0 — общее среднее; — эффект фактора различия повторных испытаний (/ = 1, a); Zy ~ 7V(o, Gq) — ошибки измерения, распределение

которых принимается нормальным с нулевым математическим ожи­
данием и равными дисперсиями Oq; а — число сравниваемых повтор­ных испытаний; п — одинаковый объем выборки в каждом из повтор­ных испытаний.

В дисперсионном анализе рассматриваются модели эффектов фактора двух видов, а именно: модель постоянных эффектов, при ко­торой х — представляет собой некоторое детерминированное значение, и модель случайных эффектов, при которой xi имеет нормальный за­кон распределения.

а п _ 2

Рассмотрим квадратичную форму £ £ ху — > гДе оценка об-

_ j а п /=1 J=1

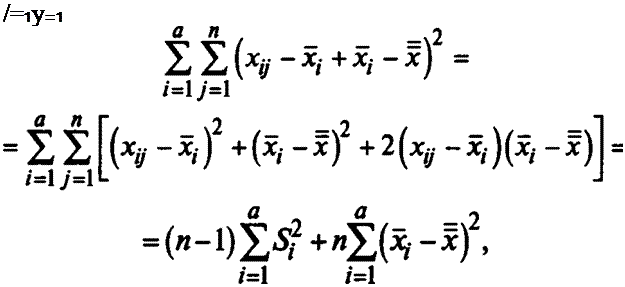щего среднего х = — У У х». Эта форма разбивается на две состав­ил ; 4

ляющие:

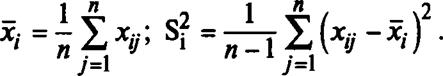где оценки среднего и дисперсии в отдельном повторном испытании соответственно равны:

В дисперсионном анализе формируются две статистики:

ЇМ? — тЧіЙ-їГ с математическим ожиданием М [sj2 ] = а — і /*_|

= пс2 + (для модели случайных эффектов) или Л/£у2^ = —+

+Gq (для модели постоянных эффектов);

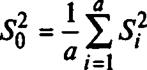
с математическим ожиданием

Проверка воспроизводимости результатов повторных испытаний проводится с использованием /’-критерия Фишера. При гипотезе воспроизводимости (xi =0 или а2 = 0) отношение £2 /Sq имеет

распределение Фишера с [д-1, а(п-1) числом степеней свободы, т. е.sl/sl — F[a-1,а (л-1)], и решающим правилом для принятия гипотезы воспроизводимости является неравенство Si Si < F, , где Fl_a — квантиль распределения Фишера уровня значимости а.

При принятии альтернативной гипотезы (невоспроизводимости) показателем воспроизводимости может служить величина S? — Sl/n, являющаяся оценкой эффекта фактора различия повторных испыта-

1 о ~ ,

ний ——— У х~ (модель постоянных эффектов) или (модель слу-

а -1 ,=1

чайных эффектов).

Приведенный подход легко обобщается на случаи неравен­ства дисперсий ошибок измерений и неравенства объемов выбо­рок повторных испытаний. Так, в случае неравенства дисперсий

о?., имеем:

Л/И-^+ItoS, — для модели случайных эффектов;

М ] — “ 7 X х? + “ X ао/ — для модели постоянных эффек — “ “1 /=1 “ /=1

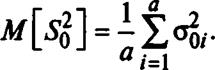тов;

Предположим, что число степеней свободы а(п-1) велико (бо­лее 120). Тогда оценку Sq можно заменить на истинное среднее зна-

1 а

чение Opp = — JOq(. и статистика /Sq будет иметь, например для

аы 1

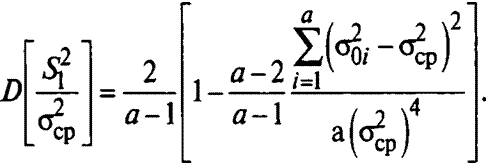модели случайных эффектов, математическое ожидание и дисперсию соответственно равными:

л

Распределение этой статистики при нулевой гипотезе = 0 — приближенно X — распределение с числом степеней свободы

а-1

v =

і а-2 1 v

1 + —-X

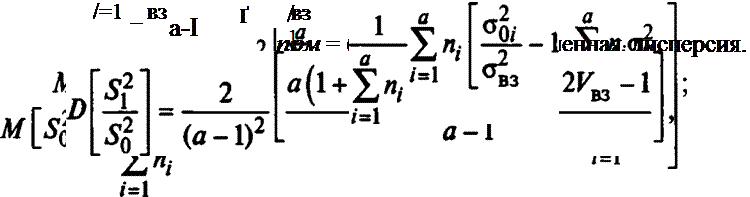Статистика /Sq в этом случае будет иметь следующие матема­тическое ожидание и дисперсию:

‘sf	і	acL ср j
kJ	а-	_<4

М

Таким образом, математическое ожидание статистики S2/Sq при

нулевой гипотезе равно 1 тогда и только тогда, когда средневзвешен­ная дисперсия равна средней дисперсии, т. е. когда все л,- равны. Поэтому приведенные алгоритмы следует дополнить критерием срав­нения дисперсий, например критерием Бартлета:

^~Х2 (я-1)>

	( , о Л	а	( а Л
где В = 2,303	vlgly2-£v,.lg. S?	; v = £v,-; S2 =
	/=1 J	(=1	[i=i j

а 1 1

I1-1

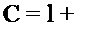v’=1 V/ Vy

Гипотеза равенства дисперсий отвергается, если В С > Xi~a-

При равенстве числа степеней свободы можно использовать критерий Кохрана:

g = maxSf/^Sf.

/ /=1

Квантили специального распределения статистики g, зависящего

от числа повторных испытаний а и числа степеней свободы V,-, табу­лированы. Нулевая гипотеза равенства дисперсий отвергается при

превышении статистикой g соответствующей критической точки ^_а.