Анализ методов проверки адекватности математической модели возмущенного движения самолета результатам сертификационных летных испытаний

Большая стоимость проведения летных сертификационных испыта­ний заставляет постоянно искать пути сокращения их объема. Одним из таких путей, широко используемым как у нас, так и за рубежом, является объединение результатов моделирования и летных испыта­ний с целью повышения достоверности принимаемых на их основе решений о соответствии характеристик самолета нормам летной год­ности [29]. При этом полноправное использование результатов моде­лирования требует прежде всего проверки адекватности математичес­кой модели самолета.

При проверке адекватности математической модели самолета выделяют два аспекта: детерминированный и статистический. Будем исходить из того, что уравнения движения самолета с системой уп­равления, составленные по результатам аэродинамических продувок и ожидаемых характеристик используемой аппаратуры (с учетом ре­зервирования и работы системы контроля), адекватно отражают ди­намику процессов управления, а в проверке нуждается математичес­кая модель, используемая для статистического моделирования с целью оценки точностных характеристик систем автоматического управле­ния. При этом полный диапазон возможных изменений оценивае­мых параметров движения самолета делится на области: больших оши­бок управления (±4-5а) и малых ошибок управления (±2-За). Рассмотрим область малых ошибок управления.

Действующие на самолет возмущения чаще всего являются нор­мальными случайными процессами. Динамическая система «само­лет-система управления» в малом диапазоне изменения ее перемен­ных квазилинейна и обладает свойством нормализовать проходящие

через нее сигналы. Все это позволяет в диапазоне (±2 — За) считать распределение ошибок управления нормальным [52]. Статистичес­кое моделирование проводится с учетом имевших место в летных ис­пытаниях случайных факторов (масса, центровка, ветер и т. д.) как в части диапазона их изменения, так и частоты появления различных
уровней. Летные испытания статистически независимы и охватыва­ют ожидаемые условия эксплуатации. Будем считать, что математи­ческая модель и реальный объект статистически подобны (статисти­чески однородны), если расчетные и опытные выборки извлечены из одной и той же генеральной совокупности.

Биномиальный закон распределения генеральной совокупности. Исходной информацией при использовании биномиального закона распределения для определения вероятности нахождения исследуе­мой характеристики в допустимом диапазоне, оцениваемой по час­тоте этого события, является число испытаний Hq и отказов d0 при статистическом моделировании и числа испытаний п и отказов d в летных испытаниях. Если оцениваемые вероятности Rq, R не равны,

т. е. если Rq*R, то вероятность события (</0, d) представляет собой

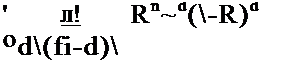совместную вероятность двух независимых событий d0 и d:

При Rq = R результаты моделирования и летных испытаний мо­гут быть объединены, что приводит к объединению выборок (d0 + d), (л0 + л) и совместной вероятности

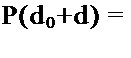________ Ч+я)!___________ R(r^+n)-{d0+d) (1 _ R,(d„+d)

(d0 +</)![Ц) +л)-Ц) +</)]!

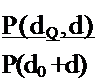Отношение этих вероятностей при Rq = R имеет гипергеометри­ческое распределение:

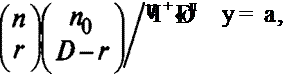Если альтернативной гипотезой является гипотеза R < Rq, то об­ластью принятия нулевой гипотезы Rq = R является область, ограни­ченная условиями

где D = d0 +d, а — выбранный уровень значимости.

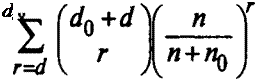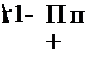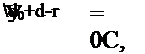Используя биномиальную аппроксимацию гипергеометрическо­го распределения, получаем:

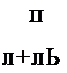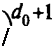откуда при выборе d = 1 имеем простое соотношение для планирова­ния числа летных испытаний:

Таким образом, для принятия гипотезы однородности минималь­ное число летных испытаний до первого отказа должно определяться равенством:

1-V)irs

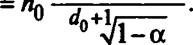п

Так, при а = 0,1; = 0; Лц=46 имеем я = 5.

Достоверность принимаемых решений характеризуется вероятно­стями ошибок первого а и второго |3 рода (вероятностями ошибоч­ных приемки и браковки). Для определения значения р необходимо задать альтернативную гипотезу и соответствующее ей распределение, что в общем случае при произвольных dvid^ сделать достаточно сложно и не позволяет получить аналитическое решение.

Нормальный закон распределения генеральной совокупности. Тра­диционные критерии статистического подобия двух выборок, извле­ченных из нормально распределенной генеральной совокупности, основаны на сравнении дисперсий и математических ожиданий [52]. Дисперсии считаются равными, если выполняется правило (крите­рий Фишера):

(15.5)

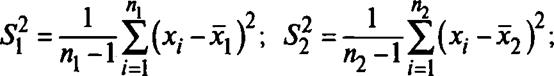где выборочные оценки дисперсий соответственно определяются как

Xj — значение исследуемого параметра в /*-м эксперименте (вычисли­тельном или летном);

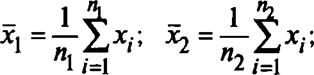«і, «2 — объемы выборок; -1, п^-1) — квантиль распределе­

ния Фишера с (й| -1, /ij -1) числом степеней свободы уровня (1-а); в

числитель помещается большая из оценок S2 > S2.

Для сравнения математических ожиданий используется одно из следующих правил:

1*1~*2І Syj(n +nl)lnn2

• при принятии гипотезы равенства дисперсий

где s2 =[*У12(Л1 — 1) + Sj(/*2 — 1)]/(л! +«2-2); +л2-2) — квантиль

распределения Стьюдента с (п1+п2-2) числом степеней свободы уров­ня 1-а/2;

• при принятии гипотезы неравенства дисперсий

*1 "*2

^l/nl + S2/n2

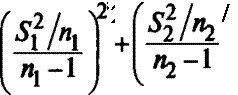где число степеней свободы v определяется в соответствии с прави­лом Сэттервейта:

и в зависимости от конкретных значений S2 и S2 меняется в диапа­зоне ma{nvn2}<v<{nl+n2-2).

Применение решающих правил (15.5) и (15.7) в случае статисти­ческой неоднородности сравниваемых выборок позволяет выявить ис­точник неоднородности — систематические или случайные ошибки.

При проверке равенства дисперсий альтернативную гипотезу удоб­но представить в виде а2 =5о2- Тогда зависимость между а, р, 5, nlt определяется из граничных соотношений:

Sl /S2 = F-cSn ~ 1. «2 "

S /5^2 = F$(n “I — ^2 -^)>

откуда «расстояние» между нулевой и альтернативной гипотезами

5 = F-a^n ~1> "2 ~iyF^ni -1. «2 -!)•

Таким образом, при принятии гипотезы равенства дисперсий с вероятностью р эти дисперсии могут различаться в 8 раз. Таблица 15.4 иллюстрирует зависимость величины 8 от пх = и2 = п ПРИ

а = р = 0,05.

V	10	20	30	40	60	120
5	8,870	6,240	4,392	2,860	2,354	1,828

Зависимость коэфф

III.

евта 5 от v

Таблица 15.4

При проверке равенства математических ожиданий альтернатив­ную гипотезу удобно задать в виде т1=т2+ 8. Тогда при альтернатив­

8 Иі+«2

пределение с параметром нецентральное™ — ,|——-.

ау пхП2

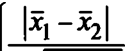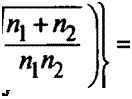Нецентральное распределение уже при п>5 хорошо аппрокси­мируется нормальным распределение, т. е.

8 K+«2 1-а/2 »№

■f1 + {1-а/2 /2(п1 +л2-2) где Ф — интегральная функция стандартного нормального распреде­ления.

Окончательно имеем:

_5 К+”2

|_а/2 о у /Ij«2

•J1 + ^1-а/2/[2(я1 +л2 -2)]

Таблица 15.5 иллюстрирует зависимость величины 5/о от = л при а = р = 0,05.

Таблица 15.5 Зависимость отношения 8/а от л п 106 27 13 8 6 5 4 4 5/а 0,5 1.0 1,5 2 2,5 3,0 3,5 4,0

Из численных значений, приведенных в табл. 15.4 и 15.5, вид­но, что необходимый объем испытаний определяется задачей срав­нения дисперсий.

Рассмотренные критерии имеют один существенный недостаток: раздельное сравнение дисперсий и математических ожиданий приво­дит к снижению достоверности принимаемых решений, так как

1 —aL = (l-a1)(l-a2), где ava2 — уровни значимости при проверке

равенства дисперсий и равенства математических ожиданий. Так, при

выборе ctj = а2 = 0,1 a z= 0,19, т. е. увеличивается почти в 2 раза.

Закон распределения Рэлея генеральной совокупности. В [29] для демонстрации соответствия характеристик выдерживания траектории при автоматической посадке предлагается использовать максималь­ные отклонения от линии курса или глиссады, имеющие при введен­ных выше допущениях распределение Рэлея:

Р(х) = 1-ехр{-х2/(2а2)}.

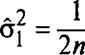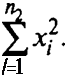Параметры а2 и а2 двух выборок считаются равными, если вы­полняется правило: о2 /о2 < /j_a (1пх, 2л2), где выборочные оценки параметров распределения Рэлея имеют вид:

Зависимость между а, р, к, п^, п2 определяется из граничных соот­ношений

blb=Fx_a{2n{y2n2),

в? /(Sdl) = ^р(2"1’2я2)-

откуда находится расстояние между нулевой и альтернативной гипо­тезами:

8 = W2"l — 2л2 )/М2и1 — 2*2 )•

В табл. 15.6 приведены значения 8 в зависимости от п^=п2=п

при а = р = 0,05. Сравнение табл. 15.4 и 15.6 показывает, что оценка параметра распределения Рэлея производится по «двойной» выбор­ке. Это приводит к уменьшению необходимого объема испытаний и повышению достоверности статистического решения.

Таблица 15.6 Значение 8 в зависимости от л п 5 10 20 30 , 60 6 4,646 2,895 2,103 1,831 1,532

Проверка адекватности с использованием толерантных интерва­лов. Проблема множественного сравнения может быть решена пере­ходом на сравнение толерантных интервалов.

Так как оценка К = (xa-x}lS имеет приближенно нормальное распределение с математическим ожиданием М[К] = UR и дисперси­ей D[K] = l/n+K2/2(n-l) ,то задача сравнения статистической одно­родности двух выборок сводится к сравнению двух математических ожиданий при известных неравных дисперсиях. Соответствующее ре­шающее правило имеет вид:

(15.8)

При использовании решающего правила (15.8) альтернативная гипотеза задается в виде URl = UR2 + AUR. Тогда зависимость между а, р, AUrv Пу, п2 определяется из граничных условий

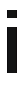*1

кх-К2 +AUR/^jDi+D2 = Up, откуда получим AURj^I+D2 = Ux_a, 2 — Un

В табл. 15.7 представлена зависимость величины AUR/JDl + D2 от Л[ = л2 = л при а = Р = 0,05.

Таблица 15.7 Зависимость ДUR JD^+Щ от л п 44 11 5 3 2 AUR/yjDl+D2 0,5 1,0 1,5 2 2,5

Для сопоставления полученных результатов приведем их к еди­ной шкале путем вычисления ошибки при оценке вероятности на­хождения исследуемого параметра в заданных пределах. Результаты

проведенных вычислений при заданных Д, = 0,95 и Л| = Л2 = 40 сведе­ны в табл. 15.8.

Таблица 15.8

Зависимость ошибки в оценке вероятности от метода Метод Сравнение дисперсий Сравнение математи­ ческих ожиданий Сравнение параметров распределения Рэлея Сравнение толерантных множителей Оценка вероятности 0,7167 0,799 0,789 0,9267 Ошибка в оценке вероятности 0,2395 0,151 0,161 0,0233

Таким образом, метод сравнения толерантных множителей при проверке адекватности математической модели возмущенного движе­ния самолета имеет существенное преимущество перед остальными методами.

Универсальный показатель степени адекватности. Рассмотрение приведенных критериев проверки адекватности математической мо­дели результатам испытаний показывает, что для каждого закона рас­пределения степень адекватности характеризуется конкретным пока­зателем (разность математических ожиданий, отношение дисперсий, разность квантилей распределения), что неудобно для сравнения и выдачи рекомендаций по использованию этих критериев.

Универсальный показатель степени адекватности, робастный к виду критерия, может быть получен на основе анализа влияния уров­ня значимости 0<а<0,5 на процедуру принятия решения об адек­ватности. При а ->0 область принятия гипотезы адекватности рас­ширяется, и любые данные моделирования и испытаний признаются принадлежащими одной выборке. Таким образом, если гипотеза адек­ватности принимается при малых значениях а, то соответствующая степень адекватности мала. Аналогично, если гипотеза адекватности принимается при больших значениях а-»0,5, степень адекватности велика. Следовательно, критическое значение ос^, при котором еще принимается гипотеза адекватности, может служить универсальным показателем степени адекватности. Проиллюстрируем предлагаемый подход на наиболее простом примере биномиального распределения.

Пусть п = л0, тогда ос^ = 0,5; при л0 = 46, п = 1 ~ 0,02. Более

наглядными являются нормированные значения а* = /0,5. Тогда в

первом случае а* = 1, а во втором — а* = 0,04.

Показатель степени адекватности необходимо учитывать при объе­динении данных моделирования и испытаний. Для такого объедине­ния рассмотрим две гипотезы: адекватности с вероятностью а* и

неадекватности с вероятностью 1-а*. Тогда в соответствии с форму­лой полной вероятности получим, например, для биномиального распределения

A-^a-aW.

где Rqб = (я*о +лі)/(лд + л) — оценка, полученная в результате объеди­нения данных моделирования и испытаний (щ = л0 — </0, m = n-d); Джс = т1п ~ °Ценка> полученная только по результатам летных ис­пытаний.

(1-а*)У- ~0г(п-г)

яга-*/*

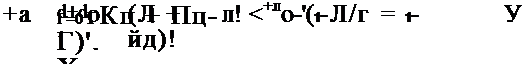Аналогично получим правило подтверждения требований к за­данной вероятности Л, с использованием нижней доверительной гра­ницы

При отсутствии отказов (d= dQ = 0) это выражение приобретает

(l-a)R^ +а* J^+n° = 1-у,

откуда Rз = (1 — y)/[l — a* + а* (1 — у0)] = 1 — уэкв, где = 1 — у0 — пра — вило подтверждения заданного значения R^ при проведении модели­рования объема л0; у0, У» Уэкв — соответствующие доверительные ве­роятности.

Поскольку знаменатель 1 — а* + а* (1 — у0) всегда меньше единицы,

значение уэкв всегда меньше у, следовательно, объединение инфор­мации всегда позволяет сократить число летных испытаний.

В табл. 15.9 приведены результаты расчетов числа лад, летных испытаний до пёрвого отказа (d = 1), необходимых для проверки адекватности, и пл — для подтверждения требований к вероятности Rз = 0,95, у = 0,9 по результатам объединенных испытаний при

nQ = 46, dQ = 0.

Таблица 15.9 Результаты расчетов числа летных испытаний лад и пл "ад 5 10 20 30 46 а 0,2 0,35 0,57 0,74 1 Уэкв 0,87 0,85 0,8 0,66 0 ил 41 36 31 20 0

Нетрудно видеть, что лад =пл « 25, т. е. « п0/2 хватает и для про­верки адекватности и для подтверждения заданного значения вероят­ности при условии, что это значение подтверждено результатами моделирования.

[1] Центральный аэрогидродинамический институт.

Рис. 8.2. Стратегия поиска и изучения особенностей динамики и управля­емости опытного самолета при летных испытаниях и установление допус­тимых эксплуатационных границ

[3] R = £/2, т. е. величина среднего риска при ц < 1 и I; £ 1 — т| не зависит от у.

Приведем далее уравнение, полученное для расчета оптималь­ной величины контрольного допуска и учитывающее корреляцион­ную зависимость между у и 5, для нормальных плотностей вероятно­стей /і (у) и /2 (5). Пусть эксплуатационный допуск на параметр является симметричным, тогда уравнение оптимальной величины кон­трольного допуска будет иметь вид:

[4] правило браковки системы