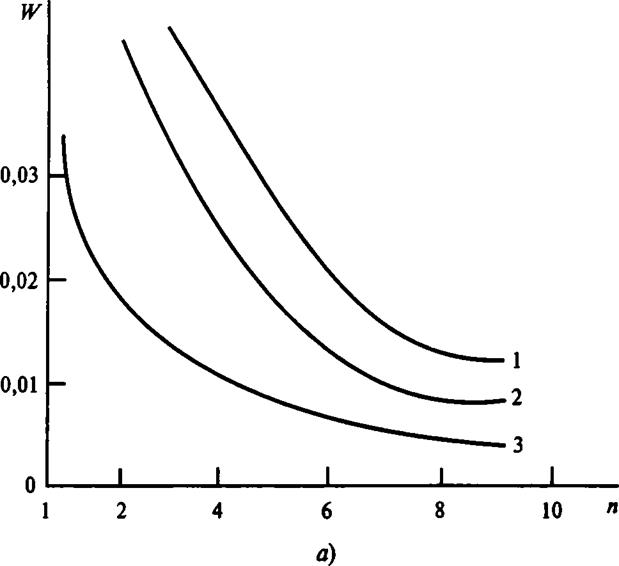
Планирование объема испытаний при использовании байесовского метода

Байесовский метод оценивания в традиционной форме используется для анализа результатов испытаний и не приспособлен для решения задач планирования. Действительно, методика байесовского оцени­вания показателей эффективности системы основана, по существу, на использовании эмпирического байесовского подхода, при кото­ром априорная плотность распределения P(R) определяется по пред­варительным экспериментальным данным. Такой подход применим лишь в случаях, когда оцениваемый показатель эффективности при переходе на следующий этап отработки не измеряется по какому-либо неслучайному закону. При выполнении этого условия для подтверж­дения заданной вероятности достаточно проведения необходимого объема предварительных испытаний, последующие испытания для уточнения полученной априорной оценки не требуются.

Таким образом, целью проведения последующих испытаний мож­но считать проверку гипотезы о стационарности параметра R, кото­рая, как будет показано ниже, сводится к проверке гипотезы стати­стической однородности априорных и экспериментальных данных.

В том случае, если результаты последующих испытаний оказы­ваются однородными с принятым априорным распределением, па­раметры которого выбраны из условия подтверждения по априорным данным заданного значения показателя эффективности с необходи-

Объединенные оценки показателей эффективности, полученные разными методами Метод получения оценок Алгоритмы получения оценок Свойства объединенной оценки Выигрыш В точности Характеристика Байесовский метод оценивания P(R/X) = , P0(R)P(X / R)dR о где Pq(R) — априорное рас­пределение; Р(Х/К) — фун­кция правдоподобия измере­ний Нормальное биномиальное распределение: 1 п^> Лб=—1— X*, "о+пы Оценка по объединенной выборке (л0 + л): /І0 +Л /І0 +Л где Д),^кс — априорная и экспериментальная оценки Условие несмещенности: M[B0] = M[R3KC] = R Оценка обеспечивает минимум среднего риска оо оо W= fdxTI(R, R)P(X/R)Pq (R)dR при квадратичной функции потерь п(л, л)=(л-л)2 Степень уменьшения дисперсии зависит от вида распределения и соотношения между величиной и точностью априорной и экспериментальной оценок Имеется развитая теория байесовского оценивания. В качестве априорной информации может быть использована как статистическая, так и экспертная информация. Обеспечение несмещенности байесовских оценок требует проверки статистической однородности объединяемых данных

OS

40

U)

ON NO -tb

Метод линейного объединения 4*=1>А 1=1 Д — составляющие оценки; ос, — весовые коэффициенты Условие несмещенности: Xа/ =1; Л/ГД1 = Л; / = 1……….. /t м Условие эффективности: 1 / 1 ai = d г*—’ / ы где dt — дисперсия оценки Д При равных dj do6 _ 1 dt к Частный случай байесовской оценки Обобщение байесовских оценок при неоднородных объединяемых данных 46=Jp^+(i-Jp)4KC. где Р — вероятность од­нородности объединя­емых данных Величина смещения для оцен­ки по объединенной выборке: Д=±Р ЦР), /^+/1 где 8(Р) — погрешность стати­стического решения об одно­родности. При Р-> 1 Д->0 ddo _pl, ^ЭКС ^экс +(1 — р)1 (ниже точности байесовских оце­нок) Требует (на основе использования критериев статистической неоднород­ности) расчета вероятности Р Метод коррелиро­ ванных процессов A*=АКкс+RRo+CR’ А где — модельная оценка; R — известное при модели­ровании истинное значение: А Аэб^кс-^К-*). Условие несмещенности: В+ С =0 Условие эффективности: ^ = Ао/Аю» где Z)jq — ковариация между экспериментальной и модель­ной оценкой; /)00 ~ дисперсия модельной оценки 4об _ 1 4.КС І-‘-2’ VAlAx) коэффициент кор­реляции В качестве априорной информации могут быть использованы только резуль­таты моделиро­вания с извест­ным истинным значением R

 

	Джс- ni=1 Ао =~S(^kcx _ Акс)(% ~ А’ ^оо=^1К/-Л)2. "(=1 пЫ 1			Замена истин­ных неизвест­ных /)10, D0о их оценками приводит к снижению точности объединенной оценки
Метод параметри­ ческих функций	4б = ^0 + ^1 Дэкс ’ А Л *об = ^0 + ^экс ’ А А ^об "" ^1^ЖС’ Я-рХо — параметрические функ­ции, определяемые на основе априорной информации из ус­ловия обеспечения желаемых свойств оценок	При мультипликативной модели из условия среднего риска для биномиального распределения х. 1 , muo~m(r2) пм[яЧ	И’об 6л ^ЭКС 3(1 + 2//) ^об _ 6(л + 2) «"б 3(1 + 2я) (ниже точности байесовских оценок)	Автоматически учитывает воз­можную неодно­родность объе­диняемых данных. Пара­метрические функции имеют сложную нели­нейную зависи­мость от момен­тов априорного распределения, полученную лишь для про­стейших случаев

мой доверительной вероятностью, требования к показателю эффек­тивности можно считать подтвержденными.

В качестве статистики для проверки гипотезы однородности при подтверждении требований к вероятности выполнения задачи может быть использовано число успехов т при проведении испытаний. Тео­ретическим законом распределения этой величины является безус­ловное распределение Р{т), учитывающее как априорную, так и эк­спериментальную информацию. Слишком малые или слишком боль­шие значения т говорят о том, что экспериментальные данные не согласуются с принятым априорным законом распределения эффек­тивности. Однако использование такой статистики не позволяет пла­нировать число испытаний.

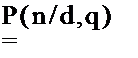Более удобной в этом отношении является статистика — число я испытаний до получения заданного числа отказов. Если число отка­зов d зафиксировано, а число испытаний является случайной вели­чиной, то функцией правдоподобия является распределение Паскаля

где q = l-R — вероятность отказа.

Априорным распределением для вероятности отказа является 13-

распределение с параметрами Уо > ‘По :

Р(д) = В{у0,ц оУ10"1^-?)70"1-

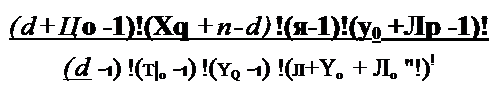Безусловное распределение числа испытаний до заданного числа отказов d представляет собой бета-паскалево распределение:

Значения нижней и верхней границ критической области опреде­ляются из условия:

Вер{я^лв} = Yi» Вер{я<лн} = 1-у2,

где у. + у — -1 = у ~ заданная доверительная вероятность.

Так как таблиц бета-паскалева распределения не существует, то для практических расчетов удобно использовать биномиальную апп­роксимацию интегральной функции бета-паскалева распределения при условиях d « л, т|0 « у0 +т|0, л « у0 +т)0 — 1, </ + т|0 « max{Yo +Ло*я}:

 

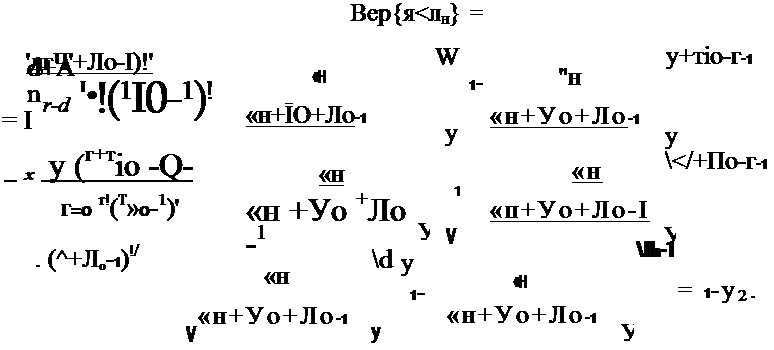Для верхней границы с учетом дискретности распределения имеем:

Вер{л £ л,,} = 1 — Вер{л й «3}+Вер(яв) = Yi,

гле Prnfrt/1- (^+11о~1)!(‘Уо+яв~</~1)!(яв~1)!(уО+11о~1)!

(</-і)!(л0-1)!(«в -^ЖУО -^("в +У0 +Ло -1)1

Минимальное число испытаний, необходимое для проверки ста­тистической гипотезы о соответствии-экспериментальных данных ап­риорному распределению, будет не менее ян. Для высокоэффектив­ных изделий необходимое число испытаний удобно рассчитывать, исходя из числа испытаний до получения первого отказа.

При выборе d = 1 формула для односторонней нижней границы преобразуется к простому виду:

1-[1-ян/К+Уо +Л0 — I)]110 = 1~У>

откуда находим

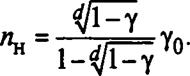Простой вид для нижней границы получается также при Ло = 1:

Нетрудно видеть, что при y0=riQ-d0, Ло=^о + 1 полученный критерий проверки статистической однородности совпадает с крите­рием проверки равенства параметров двух биномиальных распределе­ний. В табл. 14.5 приведены критерии проверки статистической од-

ON SO oo

Критерии проверки однородности параметров ряда распределений Распределение Исследуемый параметр Безусловное распределение измерений Решающее правило Паскаля R Бета-паскалево распределение (d + Ло -1)!(їо +яв -^-1)!(и~1)!(Уо +% -1)! (d — 1)!(л0 — rf)!(Yo -‘1)!(л + Yo +ТІ0-1)1 4, = о "V«SYo </ = і ^і-Л/Пмї, А "а ^ Нормальное т Нормальное распределение (2я)-1/2 ехр{-1(х-*о)2 Аэ«об}( V*o6 )V2 | | о0л/1/ло + 1/« _“Na/2’ wi-a/2 “ квантиль нормально­го распределения о2 Обратное Р-распределение 2-го рода: , ( уь/2 / г.2 Я о 2 p(s2/s2)= п 1, .xLLJ^iL. V’ г*J ^ ♦ іV V У $2 с2-/І-а(Я-ЛЬ)> ^1_а — квантиль распределе­ния Фишера

 

Для математического ожидания: • условное относительно S2 /-распре­деление Стьюдента с параметрами

-1) + »У2(я-1) п$+п «О+л-2 «о — h-ajl (^О + я ~ 2)> h-a/2 — квантиль распределе­ния Стьюдента

• безусловное относительно З2 /-рас­пределение Стьюдента с параметрами

«о п

п-1

/

Для дисперсии: • условное относительно х обратное 13- распределение 2-го рода с параметра­ми і-._______________ по+п. 2( 2%’ п-1 • безусловное относительно х обрат­ное p-распределение 2-го рода с пара­метрами afrca

(Aw to? «Ь Яо+я

‘Ъ-1) *0

ON 40

 

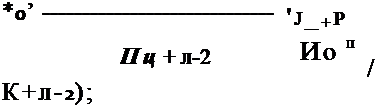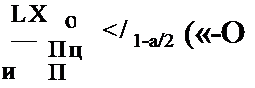нородности априорных и экспериментальных данных для ряда других распределений, выведенные на основе предложенного подхода и со­впадающие с известными в математической статистике критериями однородности параметров распределений.