Моделирование управления продольным траекторным движением самолета на Mapiupyfe

Реакция замкнутой системы «самолет — САУН» на управляющие воздейст­вия. Дополним модель вынужденного продольного короткопериодического движения самолета (3.19) уравнением траєкторного движения самолета по высоте. Пусть управляющее воздействие на руль высоты создает САУН. Управляющее воздействие по высоте формируется пилотом с помощью задатчика высоты с пульта управления САУН. Тогда модель замкнутой системы «самолет-САУН» будет содержать уравнение состояния, уравне­ния выхода и входа, а также закон управления САУН:

^лнт(^) Ajikt ХЛ£Т (t) +	(10.13)
УпктО) = Хпжт(1),	(10.14)
<,T(t) = 5£AYH(t)j	(10.15)
5САУн(г) = D^TVHynitT(t) + Еп£гУн ДНэад (t),	(10.16)

	ao>z,°	О	О
aa, rof	аа, а	О	О
	О	О	О
0	аН, а	аДЦ’	О

D“y” = [k„i 0 ku kvk”], E“v" = _ kuk„H,

Получим вектор передаточных функций замкнутой системы «само­лет-САУН» по параметрам продольного короткопериодического и траєк­торного движения на управляющее воздействие по высоте

Переходная матрица состояния по параметрам продольного короткопе­риодического и траєкторного движения самолета при включенной САУН

ф“>(Р) = (pi — А„„ + BL, D£X_1 = (Ф«ун)-1.

Переходную матрицу состояния Ф£ктУн (р) определим следующим обра­зом:

где {Ф“ун(р)-}пд-присоединенная матрица. Определитель матрицы

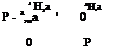Р — aG)„G>, —

р* + А$АУнр3 + А^н р2 + А? АУН р + ^ун = ДСАУн (р)>

Аз ун = A™ = 2hJP,

(®и ) — ae>2,S. aiMot >

дСАУн _ дАПи _ ■ ■ и _ — я я к кН

І сі<ое>51 асм»Е аН.« ЛН

= ^«,а ^сцс&Е **Н, а ) *

к ь *

. CAW.. АО

кД

 

Фпкт "(Р)}пр_ присоединенная матрица.

Так как вектор входа по управляющим воздействиям В^кт содержит только один ненулевой элемент аю 5 , определим в присоединенной матрице {ФиГх Н(Р)}пр только первый столбец:

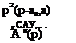
Р2»^ Р2аа, Иг(р — а^)

———— .—.———— ———— х

д САУ„, . * САУН, .

Д н(р) А н(р)

+ a^a^Jp

ан, и ааЛ

х—————————————————- —

асау„, .

А Н(Р)

Вектор передаточных функций имеет вид

Рї(Р-аа.«)аШіЛкик1>

А САУН, v

2 А ^ н

Р ^a, o)z^toz,8B и и

А СДУи/ Ч

„ Л (P) н

Р аа, шДр — aa, a)am„s, kuku

АСАУН £ ч

А н(р) н

[(аа, ю,аН, а + аі),шгаНи)р — аи, га, аНиааа] ашг6,к„ки

аСАУн(р) .

или

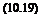„САУ„ 2 и4 р

р4 + А3АУ"р3 + аГнР2 + А^АУнр +■ АоАУ" ’

wtH“*(p) =

р[в"Унр + в? АУи]

(10.20)

 

	«Ср + В0
w£J-(p)
р4 + дСАУн рз + ДСАУ и р2 + дСАУн р + дСАУ

 

где ВГ"н(р)= -a^kukj1, В^АУн(р) = afflz, Siaa>akuk”, В, Ун (р) = — (аалан, а +

, .11 „ ГАУ,, И

+ аи, шгаН, и) a(oz,5B ки к,,, Bq (р) — ао,(ог аН, и а(ог,5в аа, а *^и

В 4 (Р) ~ a©z,5B аа, о)г^и • ‘

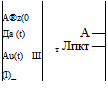
Сворачивая структурную схему замкнутой системы «самолет — САУН» (рис. 10.11) методами структурных преобразований, можно получить пере­даточную функцию (10.21).

Рассмотрим условия устойчивости замкнутой системы «самолет­САУН» по критерию Гурвица:

АзАУи = 2С>0,

АГ" = («О2 — ku > О,

А-1 = аюг,5в (au, oz аа а ^М>г^Н, а^и ao, wz ^H. u ^») > 0 .

Ар atoz,5B au, o)zaH, u аа, а > 0?

— (А^АУн)2 Ао АУн > 0.

Правильным выбором передаточных коэффициентов кШі, k„ и k‘ доби­ваются выполнения условий (10.22), а также обеспечиваются требуемые запасы устойчивости.

Рассмотрим реакцию замкнутой системы «самолет — САУН» на ступен­чатое отклонение пилотом рукоятки задатчика высоты. После окончания переходных процессов приращения установившихся значений параметров продольного короткопериодического движения примут нулевые значения:

ш

(Дю2)уст = Нт [рДНзад(р) W4(0"S(P)] = 0,

Р-0 ’

Дауст = Нт [р ДНзад (р) (р) ] = О,

р^0

Дозад = Нт [р ДН, ад (р) W1H,“ (р)] = О

р-0

и произойдет формирование нового установившегося значения высоты

ДНуст = Нт [р ДНзад (р) WAh"’ (р)] = р^о

litn || РДН, ад (ВГ"Р + В0САУн)___________

L Р (р4 + АслуНр3 + АслуНр2 + АсдуНр + Асду-

ДНэад ДНзад ♦

Привести (10.23) к табличному виду затруднительно. Поэтому для получения переходного процесса целесообразно использовать ЭВМ.

Реакция замкнутой системы «самолет САУн» на внешние возмущения.

Рассмотрим модель вынужденного продольного движения самолета, уп­равляемого САУН, при наличии внешних возмущений:

х„кт (I) = Ап„ хПІТ (I) + В£„ u£„(t) + B^u^ilt), (10.24)

yn. T(t) = xm(t), (10.25)

uLT(t) (10.26)

S^Ay" (I) D^yHyllI(T(t), (10.27)

где вектор входа u“IT(t) и матрица входа В‘,.т определяются выражениями (3.148)

и (3.149).

Получим матрицу передаточных функций замкнутой системы «само­лет-САУ н» по параметрам продольного короткопериодического и траек — торного движения самолета на внешние возмущения

WnKT(P) = = (pi — Ап„ — B;„D^yH)- 1 Bf]KT =Ф“ун(р)В»кт. (10.28)

^ ПЕТ 1Р)

кк(ш*о ТІрг+2Т*№

Г)р*1

Определим в качестве примера вектор передаточных функций на внеш­ний момент тангажа Лт„:

Рис. 10.11. Структурная схема замкнутой системы «самолет-система автоматиче­ского управления высотой»

(10.30)

(10.31)

 

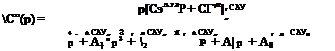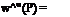гсАУ„ ГСАУИ

М р + Со

razB ‘*u, coz “а, о>г >

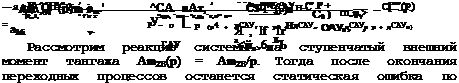
р4 + А^Ун Р3 + АГЇН Р2 + АГЇН Р + АІ

Следовательно, САУН с законом управления (10.1) является статической по отношению к внешнему ступенчатому моментному возмущению по

тангажу. Увеличение передаточного коэффициента к” способствует умень­шению величины статической ошибки.

Для доказательства астатизма законов управления САУН с изодромной обратной связью в сервоприводе или интегральной составляющей по высоте можно провести аналогичное исследование.

10.2. АВТОМАТИЧЕСКАЯ СТАБИЛИЗАЦИЯ И УПРАВЛЕНИЕ БОКОВЫМ ТРАЕКТОРНЫМ ДВИЖЕНИЕМ НА МАРШРУТЕ