Примеры использования полиномиальной аппроксимации нестационарных параметров

Таблица 10.9 Вид параметра Пример устройства Математическая модель Оценки наименьших квадратов Изменение линейных размеров изнашиваемых частей Кран, вентиль, задвижка $(t)=0|/ A/ х= … лД/ ХГХ = £/2Д/2; /=1 *TZ = X/Z/A/; /=1 п Xі*. 0, = i=1 ; 1 п Х«2д< 1=1 «Xі*. X’2 /=1 Изменение усилий резания Шлифование абразивной лентой т=Єї Л где к — известно Xі**. 0, = ■=> ; Х«2^ 1=1 и*Х’*г» = <=1 X’2* /=1

При этом необходимо построить критерий для проверки адекват­ности выбранного полинома или обоснования перехода к более слож­ному виду. В том случае, если дисперсия погрешности измерений известна, для проверки адекватности используемой модели исполь­зуется статистика

Xo=S2{n-k)/ci2.

При неизвестной дисперсии погрешности измерений использу­ется статистика

Fo=S2/S2,

где Sq — остаточная сумма квадратов неполной модели; S2 — оста­точная сумма квадратов следующей по сложности модели.

Гипотеза адекватности используемой модели принимается, если

Xo^Xi-a(«-^) или Fo<F{_a(n-k, n-k-).

Применение неадекватной модели приводит к смещению оцени­ваемых параметров. При малом временном интервале смещение бу­дет незначительным. На этом свойстве основаны модификации ме­тода наименьших квадратов, «забывающие» прошлые данные. При использовании метода скользящего среднего оценка вычисляется из соотношения

j<m;

= т І Ь’ j>m,

i=j-m

где т — некоторое выбранное заранее число «забываемых» измере­ний. Дисперсия этой оценки определяется как £)(в0) =—с2 •

‘ ‘ /И

Применяются также алгоритмы, основанные на рекуррентной фор­ме метода наименьших квадратов, например алгоритм с экспоненци­альной памятью, для которого получаем рекуррентную оценку вида

во і = вом +a(*r “вам). (10.5)

где a — некоторая заранее выбранная константа сглаживания.

Поскольку операция (10.5) проводится одинаково для всех изме­рений, запишем выражение (10.5) с учетом более ранних наблюде­ний:

0О,- =аг,+(1-а)ё0/_1 =аг,+(1-а)[ёо,_2+а(г,_1-в/-2)] = — =

1-1

= а £ (1 — a)j Zi-j + (1 — a) Goo-

j=о

Таким образом, оценка fy, является линейной комбинацией всех

измерений с весовыми коэффициентами, убывающими по геометри­ческой прогрессии.

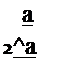Так как (1-а)’ = е_,_1п(1~а)> данный алгоритм носит название опе­ратора с экспоненциальной памятью. Дисперсия оценки с экспонен­циальной памятью при небольших значениях ос имеет вид:

Возможны и другие модификации метода наименьших квадра­тов, например число т в методе скользящего среднего может опреде­ляться не заранее, а в процессе оценивания из условия адекватности полинома нулевого порядка. Так, при известной дисперсии погреш­ности измерений о2 случайная величина (її -0Oi)/o имеет нормаль­ное распределение n(o, yj(i+l)/i, поэтому статистика (г,- -0о/)/° мо­жет быть использована для текущего выбора числа т: если выполняется неравенство

(г,—0О,)/ст<£/1-а/2,

то точка Zj включается в обычную оценку метода наименьших квадра­тов, в противном случае происходит переход на алгоритм скользяще­го среднего.

Для получения рекуррентной формы метода наименьших квадра­тов дисперсионную матрицу, полученную по /-м измерениям, пред­ставляют в виде двух слагаемых: первого, зависящего от измерений

до /-І включительно, и второго, зависящего от /-го измерения:

А = [я/-і + •

Из теории матриц известно следующее матричное соотношение:

(1р + АВ)~1 = Ip-A(lq+ ВА)~1 В,

где А — матрица размера pxq; В — матрица размера —

единичные матрицы размера р х р, q х q соответственно.

Воспользовавшись этим соотношением, получаем рекуррентное уравнение для дисперсионной матрицы:

о

При q = 1 и со=1/а выражение в скобках представляет собой скаляр и дисперсионная матрица имеет вид

Di. lXrXfDf. і

о2 + X, D,.iXj’

Для получения рекуррентного выражения оценок представляем в виде двух слагаемых оценку полученную по / измерениям:

®< — А (■*?Щ-l^i-l+ Xf (HjZj j.

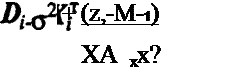Отсюда с учетом выражения для дисперсионной матрицы имеем:

ИЛИ

0, — 0|-i + AXj©,• (Z, — ).

Рекуррентная форма метода наименьших квадратов совпадает с выражением фильтра Калмана.

В [27] показано, что оценки наименьших квадратов являются состоятельными, несмещенными эффективными оценками парамет­ров линейной модели при произвольном распределении погрешнос­тей измерений, имеющем конечные значения дисперсии.