ФОРМИРОВАНИЕ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ НА НАДЕЖНОСТЬ

13.1. Основные показатели безотказности

Отказ технической системы — это случайное событие, обусловлен­ное большим числом непредсказуемых факторов. Время от момента включения оборудования до его первого отказа также представляет собой случайную величину.

Наиболее общей характеристикой надежности является вероят­ность безотказной работы Pit) = Р{% > t} — вероятность того, что на­работка до первого отказа превысит некоторое время t. Вероятность безотказной работы — монотонно убывающая функция в интервале (0,1). Часто вводится также показатель qit) = — Pit) — вероятность того, что отказ произойдет после включения оборудования через про­межуток времени, не превышающий t. Это монотонно возрастаю­щая функция времени.

Скорость изменения вероятности безотказной работы характери­зуется плотностью вероятности момента первого отказа:

dt dt

Вероятность безотказной работы однозначно выражается через плотность вероятности:

Pit) = (oit)dt.

t

Использовать в качестве показателя надежности функцию време­ни неудобно, поэтому вводятся некоторые параметры, определяю­щие эту функцию:

• средняя наработка до отказа, или среднее время безотказной ра­боты,

оо

X = (o(t)/P(t).

Интенсивность отказов имеет характерную для различных этапов жизненного цикла системы форму. На начальном этапе приработки — это убывающая функция, на этапе нормальной эксплуатации — кон­станта и, наконец, при износе оборудования — возрастающая функ­ция.

Основные выводы статистического анализа надежности получе­ны для случая X = const, когда вероятность безотказной работы P(t) = exp {-А,/}, т. е. соответствует экспоненциальному распределению времени безотказной работы.

Испытания на надежность могут проводиться по одному из основных планов (ГОСТ 16504—74):

[NUr] — без замены отказавших образцов и прекращением испы­таний после отказа заданного числа образцов г,

[NMr — с заменой отказавшихся образцов и прекращением ис­пытаний после отказа заданного числа образцов г,

[NMT — с заменой отказавших d образцов и прекращением ис­пытаний в заданный момент времени Т,

[NUT — без замены отказавших d образцов и прекращением испытаний в заданный момент времени Т.

В табл. 13.1 приведены выражения для точечных и интерваль­ных оценок среднего времени безотказной работы (средней наработ­ки на отказ) и интенсивностей отказов для перечисленных планов.

План [NUr], Плотность вероятности того, что в моменты време­ни откажут 1,…, /,…, г образцы, а остальные образцы в

интервале времени (0, tr) не откажут, имеет вид

(n-r)

f f r — It П Xe Kti /=1 V /

E */+(«-

/=1

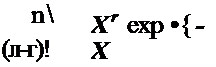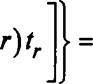
Выражения точечных и интервальных оценок средней наработки на отказ и интенсивности отказов

для различных планов испытаний на надежность

Таблица 13.1 План Суммарная наработка Несмещен­ная точеч­ная оцен­ка средней наработки на отказ Интервальная оценка средней наработки на отказ Несмещенная точечная оценка интенсивности отказов Интервальная оценка интенсивности отказов NUr £’/ + (л-Фг /=1 !л г Г 2к 2tz 1 X(1+y)/2 (2r) ’ %(1-у)/2 (2r) г-1 X(1-y)/2 (2г) 5t(l-Y)/2 (2r> 2/j; 2/j NMr ntr І г г-1 » NMT пТ fl г + 1 .4n)/2(2r+2)’ ^(1+y)/2 (2^)_ г X(1-y)/2 (2r) X(I+y)/2 (2г + 2)1 2/^ NUT ±ti+(n-r)T / = 1 Г + 1 г-1 *1 »

X */+(«-‘К

1

ср L<=1

 

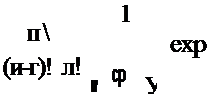Т =

*ср

и для интенсивности отказов X: X = r/t%, где Гу — суммарная наработка.

Для анализа свойств оценок Г_ и £ необходимо получить их рас­пределения. Для этого вводим новые переменные: = ^; Y2 = /2 — /j;

…; = tr_j. Тогда плотность вероятности Д/j, …, Гг) преобразуется

к виду

P(Yv…,Yr) = пХе~пХГ< (n-l)Xe~Un~l)YK..(n-r+ l)Xe~Un~r+W’

и будет представлять собой произведение экспоненциальных распре­делений Р (Yj/X) = (л — / +1)Хе_(л_,+1)ху< с параметрами (л — / +1)X.

Таким образом, переменные Tj,…, Yr — независимы.

Заметим, что выборка Т]……………. YT неоднородна, так как парамет­

ры распределений составляющих ее элементов различны.

Переходом к переменным Z, = (л — і +1) Yj преобразуем выборку в однородную с постоянным параметром X экспоненциальных рас­пределений составляющих ее элементов. На основе связи между экс­поненциальным и у-распределением нетрудно получить следующий результат:

^(n-i + l)Y, =Х//+(й-Г)/г =’г>

1=1 1=1

т. е. сумма случайных величин (п — і +1) Yi имеет у-распределение I рода:

л Г, Г-1 ^ *у — X/.

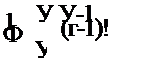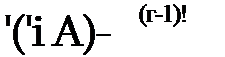с математическим ожиданием Л/[/г] = гГ^ и дисперсией />[/х] = гГІ,. Отсюда следует, что оценка 7^, = t^/r несмещенная, так как Л/Г7ср1 = = M[tT/r = rTcp/r = Tcp и имеет дисперсию = D[tz]/r =

=<А2=4А-

В соответствии с неравенством Рао-Крамера вычисляем:

т4

ср

И Проверяем условие ^[/ср 1 = 1//.

оо — оо Л г fr-2 = rJ ~P(*I /X)*I = ri / е о’х 0′ 1)-

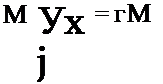Отсюда следует, что оценка 7^, эффективна. Для определения свойств оценки X найдем математическое ожидание:

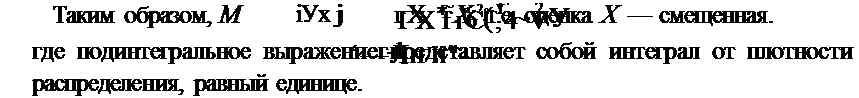Заменой переменной Y = Х/т получим

Дисперсия оценки % определяется как

Хг tr ^ — Xt, е * atт =

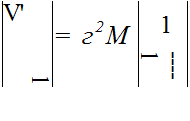
Л2

0(г-1)! — (r-l)z(r-2)

Вычисляя / = rX2, убеждаемся, что эта оценка неэффективна. Нетрудно получить несмещенную оценку 1′ = (г-1)//т с дисперсией Z>[x’] = X2/(r-2)<

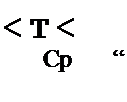
Используя плотность распределения суммарной наработки, оп­ределяем доверительные интервалы для параметров Г— и X. Введя переменную 2гГср Ас? “ — 2/£ /Тср = 2Xtz путем преобразования плот­ности вероятности /,(/£/Т’ср), получим х2-распределение:

/ л 2rTQp	1	^____	г-1 pvn 4
Тср )	2(г-1)!	т 1 ср ^ )	vAp 4

гТ,

ср

ср

Отсюда, задаваясь доверительной вероятностью у, определяем у%- ный доверительный интервал для Т‘.

и для X:

.4-гyiW

2U ~ ~ 2U

где X(i-Y)/2 (2г) » Х(щ)/2 (2г) — квантили х2-распределения.

А

Зная оценки среднего времени безотказной работы или ин­тенсивности отказов X, можно дать оценку вероятности безотказной работы:

R(t) = e ^ .

Заметим, что даже при несмещенных оценках 1 оценка R сме­щена вследствие нелинейной ее зависимости от X. Однако для высо­конадежных изделий вероятность безотказной работы — линейная фун­кция интенсивности отказов R (/) = 1 — Xt, поэтому оценка R(t) = -it будет несмещенной.

Подстановкой в выражение для R(t) нижних и верхних границ для Т„ или X определяются у%-ные доверительные границы для ве­роятности безотказной работы:

S’K‘ < R(t)< e X*{.

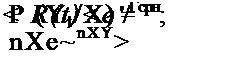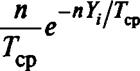План NMr. Если отказавшие изделия заменяются, то выборка интервалов между отказами становится однородной. Любой элемент этой выборки подчиняется распределению

а совместное их распределение имеет вид

P{YV..„ Yr/X) = П P(Yt/X) = (п/Т^expj-^/7^} = (пХ)гехр{-л^г}-

Логарифмируя, дифференцируя соответственно по 7J_ или X и приравнивая результат к нулю, получим точечные оценки максималь­ного правдоподобия для среднего времени безотказной работы Т~

±*ъ, ,

f _м_________ ntr _h

и для интенсивности отказов X: X = r/t^.

Свойства оценок полностью идентичны свойствам оценок плана [М/г].

План [NM7]. Плотность вероятности того, что в моменты време­ни /j,…, tr откажут 1,…, г образцы, а в интервале времени (tr 7) отказов не будет, для плана [NMT, по аналогии с планом [NMr, запишется как

П

,trjX)= П лА. ехр{-лХ(/( )}ехр[-иХ[7’-/г]} =

= (пХ)г ехр{-лХТ},

где сомножитель ехр{-лЯ,(7′ -<‘г)} определяет вероятность того, что в интервале (tr, 7) отказов не произошло.

Логарифмируя, дифференцируя по X и приравнивая результат к нулю, получим точечную оценку максимального правдоподобия для интенсивности отказов X: X = r/nT = r/t^ и для среднего времени бе­зотказной работы Т’ Tcp=t^/r.

Для анализа свойств полученных оценок используем известную связь между экспоненциальным и пуассоновским распределениями. Если наработка на отказ является случайной величиной, распреде­
ленной по экспоненциальному закону с параметром X, то число от­казов в интервале длительностью t является случайной величиной, распределенной по закону Пуассона с параметром Xt, т. е. если

P(t) = Хехр{-Х/}, то P(r) = (Xt)r exp{-Xt}jr

Рассматривая вероятность наступления отказа в элементарных интервалах Yi и учитывая, что сумма г случайных величин, имеющих

распределение Пуассона с параметром Xi, также имеет распределе-

г

ние Пуассона с параметром X = У X,- в интервале времени (0,7), по — лучим ~

P(r / пХТ) = (”?l7’)r exp {-/А Г} = {XtJ ехр{-Х/£}

‘ ‘ г г!

с математическим ожиданием М[г] = пХТ = Xtz и дисперсией Z)[r] = = пХТ = Х/£.

Вычисляя математическое ожидание и дисперсию оценки X по формулам

М[Х] = М[г]/(пТ) = пХТ/(пТ ) = X,

D [х] = D [г]/(лГ ) = пХТ/ (п2Т2 ) = Х/пТ = X/t%

и проверяя равенство J = пТ/Х, устанавливаем несмещенность и эф­фективность оценки X.

Можно показать, что несмещенной точечной оценкой 7J_ явля­ется оценка

%р =nT/r+l = t^/r+1.

Используя известную связь между интегральными функциями распределения Пуассона и х2-распределения, нетрудно получить у%-ный доверительный интервал для Т~

2 tz < 2tz

Х(2щ)/2 (2г + 2) СР Х(1_у)/2 (>)

и для X:

*(|-»1Р > ,, , *(Щ)/2 <2′ + 2>

2/j.

План [NU1]. Плотность вероятности того, что в моменты време­ни /j,…, tr откажут 1,…, г образцы, а в интервале времени (tr, 7) отказов не будет, запишется, по аналогии с планом [NUr], как

Л!

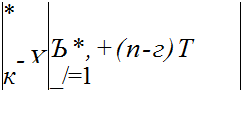
(л-г)!

Оценки максимального правдоподобия для X и Г имеют вид:

Исследования свойств полученных оценок в этом случае сложно, так как оба сомножителя г и являются случайными величинами. Однако для надежных изделий доверительные интервалы для интен­сивности отказов X и среднего времени безотказной работы 7^ опре­деляются аналогично случаю плана [NMT. Оценкой вероятности безотказной работы при использовании плана [NUT] является несме­щенная эффективная оценка вероятности R = 1-г/п, основанная на описании вероятности наблюдения г отказов в выборке объемом л с биноминальным распределением

P(f/n, R)= — — Rn~r (1 — R)r,

г! (/і — г)!

с математическим ожиданием М[г] = nR и дисперсией D[r = nR(l-R).

/Сг(1-*н)г=1-ъ; jq-r(l-R,)r

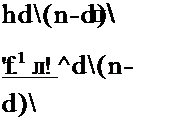Доверительные границы для вероятности безотказной работы определяются по соотношениям:

13.3. Подтверждение требований к интенсивности отказов или среднему времени безотказной работы при автономных испытаниях

При проверке требований формируются: нулевая гипотеза Щ: Х>Х3 или Тср й Т3 и альтернативная гипотеза Н{: Х<Х3 или > Т3.

В соответствии с выражениями доверительных границ интенсив­ности отказов получим решающее правило для принятия альтерна­тивной гипотезы:

t ^ Xl-a(u) ІІТПІ. . v2 /,лТсрз Ъ>—2X /I>5Cl-a W-jjn»

где значение /z и число степеней свободы > зависят от плана испыта­ний. Так, для планов типа [NM(U)r] имеем х> = 2г, а для планов типа [NM(U)T — — о = 2г + 2. Точность принятого статистического реше­ния определяется по формулам

„л„

В табл. 13.2 приведены значения показателя точности статисти-

~2 /^4

ческого решения К = ‘ при ошибках первого и второго рода

ХрО>)

a = р = 0,05 и различном числе отказов для планов типа [NM(U)r и [NM(U)7].

Значения показателя К в зависимости от числа отказов

Таблица 13.2 г [NM(U)r] іш(ит г [NM(U)r] [NM(U)J] 1 58,4 13,35 6 4,02 3,6 2 13,35 7,7 7 3,6 3,3 3 7,7 5,67 8 3,3 3,07 4 5,67 4,65 9 3,07 2,89 5 4,65 4,02 10 2,89 2,75 Таким образом, планы [NM(U)T характеризуются меньшей по­грешностью принимаемого статистического решения. Пример. Испытываются 50 изделий, получено 5 отказов и зафиксиро­ваны моменты их возникновения: tx = 19 ч, t2 = 43 ч, Г3 = 87 ч, tA = 91 ч, /5 = 100 ч. В табл. 13.3 приведены результаты расчетов суммарной наработки сред­него времени безотказной работы, интенсивности отказов и ее 90%-ной односторонней верхней доверительной границы для рассмотренных планов.

Таблица 13.3 Результаты расчетов показателей надежности для различных планов План ‘г .ч A Т’ср. Ч &,ч 1 Ч’ч"‘ NMr 4840 968 0,827 ИГ3 1,65 10"3 NMr 5000 1000 0,8 ИГ3 1,6 10_3 NMT 5000 1000 1 • 10_3 1,95-10-3 NMT 4840 968 0,827 • 10‘3 1,89 103

Таким образом, в зависимости от плана испытаний максималь­ная вариация оценок интенсивности отказов составляет 25%, а вари­ация верхней доверительной границы — 20%.