С УЧЕТОМ БЕЗОТКАЗНОСТИ

При эксплуатации АС к очередному моменту проведения работ по восстановлению вероятность отказа систем должна быть не вы­ше заданного значения. Это требование вытекает из условия обес­печения безотказности АС в полете, качества выполнения полетного задания и т. п.

Сформулируем это условие как дополнительное ограничение в системе ограничений (3.5) |15|.

В произвольный момент времени t в стационарном режиме па­раметр может находиться в состоянии і—1,2, . .., F с вероятностью

В соответствии с допустимыми решениями (3.3) возможно ли­бо провести восстановительные мероприятия, либо не. вмешиваться в работу АС. Поэтому вероятность оказаться в одном из работоспо­собных состояний /е 1, F— 1 при заданном і равна л,- "V Di}-. Из

отражающее условие, чтобы. вероятность отказа Q0 на очередном шаге не превышала некоторого заданного значения v, примет вид:

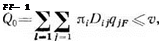
(3.29)

или с учетом (3.24)

(3.30)

Теперь задача по определению правила проведения восстанови­тельных работ с учетом указанного условия сводится к решению следующей задачи линейного программирования: определить х-1К та­кие, чтобы минимизировать значение выбранной целевой функции типа (3.20) при ограничениях (3.39) и (3.30).

Найдем область определения величины v. Из вероятностной природы величины v понятно, что верхняя граница I. Для
определения нижней границы цтщ рассмотрим матрицу вероятно­стей переходов (3.1) и выберем

qmF=mn{qiF}. (3.31)

І

Обратимся теперь к выражению (3.29) и попытаемся найти его минимальное значение. Очевидно, что оно зависит от выбора зна­чений Оі}, так как Ци? — постоянны и задаются исходной матрицей вероятностей переходов. Без снижения общности результата допу­стим, что для каждого 1=, 2,.. ., F— 1 существуют решения ви­да Dim>0 и Dih=l—Dim, т. е. в каждом состоянии і с вероят­ностью Dim осуществляется изменение состояния параметра до та­кого значения т, для которого выполняется соотношение (3.31), и с вероятностью 1—Dim выполнено любое другое изменение. Тогда

Qc = 2 rt, Dmqmp + (1 ~Dlm) qkF]. (3. 32)

i=i

В силу условия (3.31) для любого qhF—qmF+г, е>0. Тогда (3.32) примет вид:

Qo—2 яі DimqmF-{-{ Dlm) [qmF-)-e)]==e (^ nt — ^ -)-

/=i «—і /=i )

“Ь^ 1 ~ 2 (3. 33)

Из формулы (3.33) следует, что если решения для любого і вы­брать в виде распределения по возможным состояниям, то значе-

F

ние Qo всегда будет больше, чем qmF, так как 1 — ^ я;/_)(т >0.

і=і

Глобальный минимум (3.33) при выборе Dim достигается толь­ко в том случае, если Dim= 1 для всех і. Тогда

min Q0=min є ^ 1 — ^ n, Dm j + qmF=qmF-

Из этого выражения следует, что нижняя граница для величины v должна быть не меньше члена <7mF=min {qiF} матрицы вероятно-

І

стей переходов. Поэтому область определения величины v задает­ся интервалом

min {qiF} Q <. 1. (3.34)

leTTF

Рассмотрим полученные результаты. Обычно предполагается, что минимальная вероятность отказа соответствует «новому» со­стоянию параметра. Для АС это верно в подавляющем большин­стве случаев. Поэтому (3.34) можно записать в виде:

(3.35)

При выборе t)<^min {qiF} система ограничений будет противо-

І

речива, так как не существует таких Оц>0, чтобы выполня­лось (3.29).

Уменьшение величины v означает требование обеспечить на очередном шаге меньшую вероятность отказа. Этого можно до­стигнуть более частым проведением предупредительных работ. По­этому введение ограничений (3.30) может привести к уменьшению значения і*. Очевидно, что при этом возрастут средние удельные затраты, что эквивалентно снижению коэффициента технического использования (готовности). В связи с этим следует особо под­черкнуть, что при заданных вероятностных характеристиках про­цесса и затратах на восстановительные работы требования макси­мума. готовности и максимума безотказности не всегда могут быть удовлетворены одновременно. Это необходимо иметь в виду при ис­пользовании изложенной формулировки задачи. Учет вероятности отказа к очередному моменту контроля позволяет перейти к более общему критерию типа коэффициента оперативной готовности.

При введении ограничения (3.29) может измениться характер решений: возможны рандомизированные решения. При системе ог­раничений (3.5) решения Dis оказываются внутри подкласса Д’ — подкласса нерандомизированных решений. Введение ограничения

(3.29) в общем случае нарушает условия существования нерандо­мизированных решений, а это эквивалентно утверждению, что те­перь решения необходимо искать не в подклассе Д’, а во всем классе Д, что и означает возможность появления рандомизации в решениях. Докажем этот факт строго.

Рассмотрим систему ограничений (3.5). Эта система (У+1) уравнений имеет ранг F, поскольку одно из уравнений является линейной комбинацией остальных. В самом деле, просуммируем

F F F

первые F уравнений по у:зт,==0; так как для

пением, что и подтверждает высказанное утверждение относитель­но существования линейной зависимости.

Поскольку ранг этой системы равен F, то любое допустимое базисное решение задачи линейного программирования содержит ровно F положительных переменных, остальные переменные рав­ны пулю (это следует из основных свойств симплекс-метода).

Из анализа системы уравнений (3.9) ясно, что при бФ] коэф­фициенты qSj неположительны, тогда величины (1—щ) положи­тельны, а переменные xfs в силу определения (3.7) неотрицатель­ны. Тогда должен существовать по крайней мере один коэффици­ент вида (1 -—qu), при котором для всех і XiS>0. Иными словами, для каждого і существует по крайней мере одна переменная XjS>0.

Бели ДЛЯ некоторого j существуют две переменные Xjs>0, то в не­котором і-м ограничении отсутствует слагаемое с сомножителем (1 — q-a), поскольку любое допустимое базисное решение имеет ровно F положительных переменных Xis, а остальные равны нулю. Но в этом случае будет нарушено условие равенства правых ча­стей ограничений нулю или единице. Следовательно, для каждого — і существует только одна переменная Х;я>0, а остальные равны, нулю.

Введение дополнительного независимого ограничения означает изменение ранга нашей системы до Б-Н. Из общих свойств сим­плекса-метода вытекает, что в этом случае допустимое базисное решение должно содержать ровно F+1 положительных перемен­ных, а это при числе состояний в эргодическом классе ровно F оз­начает существование для некоторого і не менее двух переменных xis>0, и условие равенства правых частей нулю или единице на­рушено не будет.

Пусть для некоторого j существуют .Хд)>0 и xjp^>0, s ф р..

Ху j Хур

Тогда, используя (3. 10), получим: DJS ———————— ;БЬ =——————— .

Xjs^rXjp Xjs+Xjp

Величины DjS и Djp строго меньше единицы, что и означает суще­ствование рандомизированных решений.

Пример 3. Рассмотрим параметр, поведение которого может быть описано’ с помощью матрицы вероятностей переходов (3.16). В соответствии с (3.35) область возможных значений величины v определяется неравенством 0,03 ^н^1. Некоторые результаты решения задачи линейного программирования по мини­мизации (3.15) при ограничениях (3.5) и (3.29) представлены в табл. 3.2, где u — glgo, gu — значение целевой функции при ц=1 для заданного t>.

Таблица 3.2′ Q 0,8 0,4 0; 1 0,09 V g ■X. g X g X g X 1-0,1 0,0953 1 0,0953 1 0,0830 1 0,0818 1 0,09 0,1095 1,15 0,0998 1,05 0,0830 1 0,0818 1 0,08 0,1363 1,43 0,1144 1,20 0,0830 1 0,0818 1 0,07 0,1762 1,87 0,1231 1,29 0,0833 1,002 0,0818 1 0,06 0,2544 2,67 0,1572 1,65 0,0843 1,012 0,0818 1 0,05 0,3341 3,50 0,1920 2,01 0,0855 1,025 — — 0,04 0,4164 4,37 0,2282 2,39 0,0871 1,050 0,0823 1,008 Примечание. Для q=0,05, g=0,0631 и и=1 при всех V.

Из таблицы следует, что при о>0,1 введение ограничения-

(3.29) не оказывает влияния на значение целевой функции; прш о <0,1 наблюдается увеличение средних удельных затрат, причем! степень влияния зависит как от отношения затрат на восстанови­тельные работы Q, так и от допустимого уровня отказа и.

Полученные численные результаты подтверждают сделанный ранее вывод о том, что не всегда можно одновременно получить заданные значения безотказности и готовности. В примере 3, если безотказность удовлетворяет условию о>0,1, то будет получена максимально возможная при заданных исходных данных готов­ность. Можно также обеспечить о<0,1, но готовность будет ниже, чем в первом случае (к возрастает). Иными словами, достижение малых значений вероятностей отказа на очередном шаге требует иногда весьма существенного увеличения затрат в системе техниче­ской эксплуатации. Как следует из табл. 3.2 затраты возрастают сильнее при больших значениях q. Это обусловлено тем, что при q, близких к единице, значение упреждающего допуска близко к гра­нице области работоспособности F, и решение задачи линейного программирования. в большей мере определяется ограничениями

(3.29) . По мере уменьшения q влияние этого ограничения на зна­чение целевой функции падает, а при очень малых Q не прояв­ляется.

Аналогично ограничение (3.29) влияет. на показатели безотказ­ности, одним из которых является средний интервал времени TFF между моментами попадания в состояние F. Результаты расчетов

т Трр{уФ) л 00

величин 1FF и отношения г| =———————- представлены в табл. 3.3.

TFF(v= I)

Таблица 3.3 V Q 0,8- -0,4 |0,1 0,09 tff 4 TFF tff 1,0—0,1 10,5 1 13,8 1 18,7 1 0,09 11,2 1,06 13,8 1 18,7 1 0,08 11,5 1,19 13,8 1 18,7 1 0,07 14,3 1,36 14,3 1,04 18,7 1 0,06 16,7 1,59 16,7 1,21 18,7 1 О,0о 20,0 1,91 20,0 1,45 20,0 1,07 0,04 25,0 2,38 25,0 1.81 25,0 1,34 Примечание. Для всех значений v при q=0,05 и 0,01 соответственно равны ■25,6 и 33,3, а все Т)=1.

Для того чтобы представить характер изменения. величины x(v) при фиксированно, м q, найдем с помощью метода наимень­ших квадратов аналитическое выражение этой зависимости на ин­тервале 0,04<ц<0,11 в форме полинома:

х=а0 — f axv — f — f….. — f, anvn,

где п=2, 3, 4.

Рассмотрим результаты расчета коэффициентов полиномов ука­занных степеней, суммарной ошибки (табл. 3.4) и модуля погреш­

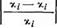(табл. 3.5), где ні — значение н из табл. 3.2;

Таблица 3.4S
	Є=0,8	q=0,4
Показатель	Степень полинома п	Степень полинома п
2	3	4	2	3	4
O. Q	10,08	9,31	3,08	4,82	5,00	2,45
а,	—175,08	— 140,04	238,07	—75,11	—83,57	70,79
а2	841,07	346,76	—7861,79	368,45	487,77	—2863,31
а3	—	2196,96	78034,98	—	-530,31	30430,05
at	—	—	252793,56	—	—	103201,06
Суммарная ошибка 8 2(хі — Хі)2	0,019	0,016	0,005	0,008	0,008	0,00&
/ = 1

Таблица 3.5 Вероятность отказа 0=0,8 0=0,4 Степень полинома п Степень голинома п 2 3 4 2 3 4 0,04 1,25 0,72 0,03 0,47 0,70 0,18 0,05 1,98 1,51 0,10 1,41 1,60 0,46 0,06 2,43 1,56 1,08 0,86 1 , 19 0,87 0,07 4,16 4,69 2,60 5,72 5,53 4,30 0,08 2,00 1,31 1,41 2,89 2,69 4,02 0,09 1,07 3,08 1,94 0,30 0,37 0,14 0,10 1,51 3,15 2,48 1,05 0,66 1,65 0,11 0,04 2,38 0,68 1,21 0,66 0,58

кі —значение х, полученное в точке і при сглаживании по методу наименьших квадратов.

Из табл. 3.4 видно, что коэффициенты при переменных />2′

существенны, а суммарная ошибка для всех выбранных п практи­чески невелика. Данные табл. 3.5 показывают, что максимальное значение модуля погрешности в диапазоне 0,04<о<0,11 не превы­шает 6%, причем увеличение степени полинома не приводит к су­щественному уменьшению погрешности. Следовательно, зависи­мость средних удельных затрат от величины v носит нелинейный’ характер, а для практических расчетов достаточно использовать уравнение ветви квадратической параболы при н>0.

Упреждающий допуск при учете ограничения (3.29) изменяет­ся следующим образом:

v…………………………………………… 1,0=0,1 0,09 4-0,08 0,07 0,06 0,054-0,04

I*……………………………………………. 7 6 5 4 3

Для большей наглядности приведем две матрицы решений (q=0,8; v— = 0,1 и о=0,05), где указаны только элементы, отличные от нулевых.

S 1……………………………………… ‘	/‘ ……………………………………………….. л
. 1…………………………………..		1……………………………………
. . 1 . . . .		0,218 . 0,782 ….
. . . 1	.	1 . . ….
. . . . 1 . .		1 . . ….
		1 . . . . .
Vі……….. ^		v…… J

Методика расчета элементов матрицы полностью соответствует изложению примера 1 § 3.1. Отличие состоит только в том, что для состояния 3 необхо­димо было вычислить два элемента: D3i и D33, появление которых дает осно­вание говорить о рандомизации решений. Кроме того, сравнение матриц нагляд­но иллюстрирует изменение значения упреждающего допуска с i*=7 до £*=3.