Сведения из теории надежности и математической статистики

При решении эксплуатационных задач на основе априорной информации приходится в основном иметь дело с анализом случайных величин (оценками пара­метров законов распределения времени безотказной ра­боты, времени восстановления и. другими оценками). При переходе к апостериорным моделям возникает необ­ходимость обратиться к анализу случайных процессов. При этом сильно возрастают требования к объему ис­ходной информации.

Если при анализе случайных величин приходится иметь дело с одномерными законами распределения, то при анализе случайных процессов необходимо изу­чать многомерные распределения. В реальных ситуаци­ях удается выбрать такие модели процессов изменения параметров авиационных систем, для анализа которых требуется меньший объем статистических данных. Поэ­тому особое внимание впредь будем уделять марков­ским, полумарковским и гаусовским процессам.

Случайные величины и законы их распределения. Одним из ос­новных понятий теории вероятностей является понятие случайной величины. Случайной называют такую величину, которая в резуль­тате опыта (испытания) принимает одно из. своих возможных зна­чений, заранее неизвестное и зависящее от случайных обстоятельств.

Чтобы полностью охарактеризовать случайную величину, необ­ходимо указать, во-первых, какие значения она может принимать, т. е. множество возможных ее значений, и, во-вторых, вероятности этих значений. Законом1 распределения случайной величины назы­вается соотношение, устанавливающее связь между возможными значениями случайной. величины и соответствующими им вероятно­стями. Закон ‘распределения .полностью характеризует случайную величину. Про случайную величину говорят, что она подчинена дан­ному закону распределения или распределена по такому-то закону распределения.

Универсальный способ представления закона распределения, пригодный как для непрерывных случайных величин, так и для дискретных — использование понятия функции распределения. Функция. распределения случайной величины F(x) —■ вероятность того, что случайная величина X примет значения, меньшие, чем х:

F(x)=P{X<x). (1.3)

Для непрерывной случайной величины закон распределения часто задается в виде плотности вероятности

f (х) =lim[F(x+Ax) —F (x)]jAx.

Ac

Между функцией распределения и плотностью вероятности су­ществуют такие соотношения:

f(x)=F'{x)-, F{x)= UWdx.

— СО

Хорошим примером случайной величины является наработка авиационной системы до отказа. Принято характеризовать эту ве­личину функцией ненадежности F(t), т. е. вероятностью того, что наработка до отказа Т меньше заданной наработки t. Ясно, что такое определение F(t) полностью совпадает с определением (1.3) функции распределения случайной величины Т. Часто применяют также функцию надежности Е(£).=11—F (£) для характеристики

вероятности безотказной работы авиационной системы в течение за­данной наработки (О, t).

Помимо плотности вероятности f(t), *в теории надежности для описания распределения случайной величины Т часто используют интенсивность отказов X(t)=f(t)IF(t). Величина Ц£) характеризует условную вероятность того, что произойдет отказ на интервале (t, t+dt) при условии, что ,в начале интервала объект был работо­способен.

Если объект после возникновения отказа восстанавливается (такой случай типичен для эксплуатации авиационных систем), то последовательные моменты отказов (и следовательно, восстановле­ний) образуют поток случайных событий. Этот поток характеризу­ется параметром потока отказов о>(£). Если случайные значения наработки между отказами одинаково распределены и независимы

(так бывает,-например, при замене отказавшего объекта — на новый), то параметр потока со (() может быть вычислен по плотности рас­пределения наработки между отказами f(t) с помощью уравнения восстановления:

t

со (t) =,f (t) + f f (t — т) со и

Параметр потока отказов по своей физической природе — сред­нее число отказов в единицу времени .наработки, взятое для рас­сматриваемого момента t. Обычно закон распределения — случайной величины (в виде функции распределения и плотности вероятности) определяется одной или большим числом постоянных, называемых параметрами, которые характеризуют центр распределения, масштаб и форму кривой распределения.

Числовые характеристики случайных величин. Случайная вели­чина — с, вероятностной точки зрения полностью характеризуется за­коном распределения. Однако при решении ряда практических задач нет необходимости знать все возможные значения случайной вели­чины и соответствующие им вероятности. В этом случае удобнее пользоваться некоторыми постоянными числами, которые дают в сжатой форме наиболее существенную информацию о случайной величине. Такие постоянные числа называются числовыми характе­ристиками случайной величины.

Многие числовые характеристики выражаются через так назы­ваемые моменты случайной, величины p, s.

Математическое ожидание (центр распределения, среднее зна­чение случайной величины) представляет собой первый начальный — момент случайной — величины.

Дисперсия случайной величины есть второй центральный мо-

ОО

мент ц2—[ЩХ]=$ (х—M[X])3f(x)dx. Ввиду исключительной важ­ности дисперсии среди других моментов для нее обычно вводится специальное обозначение Ь[Х]. Очень часто дисперсию обозначают как а2, где а — среднее квадратическое отклонение.

Среднее квадратическое отклонение -— положительное значение корня квадратного из дисперсии: a=^D[X.

Коэффициент асимметрии Sk=i3l’os — ‘При Sfc>0 правая ветвь кривой f(x) более пологая, чем левая, при 5*<0 — наоборот.

Коэффициент эксцесса Ex=i4сг4 — ІЗ. При £х>0 кривая f(x) ‘более островершинная по сравнению с кривой f(x) для нормального закона, при Ех<IQ кривая f(x) более плосковершинная, чем кривая f{x) для — нормального закона.

Нормальный закон распределения. Главная особенность, выде­ляющая .нормальный закон среди других, состоит в том, что он •является предельным законом, к которому приближаются другие законы распределения при часто встречающихся типичных услови­ях. Так, согласно центральной предельной теореме (Ляпунова), плотность вероятности суммы независимых или с-лабозависимых рав­номерно малых (играющих примерно одинаковую роль) слагаемых при неограниченном увеличении их числа как угодно близко при­ближается « нормальному закону распределения независимо от того, какие законы распределения имеют эти слагаемые. Указанные условия обычно выполняются в процессе измерений, поэтому в большинстве случаев погрешности измерений распределены по нор­мальному закону.

Нормальный закон распределения характеризуется .плотностью вероятности

1 2з*

f(x)^ —— — е ; — оосжоо,

а у 2%

где а—математическое ожидание (—оо<а<оо); о — среднее квадратическое отклонение (ст>0).

Функция ‘распределения нормального закона

х (х—а)-

F{x) = —— 1—~ J е 2°2 dx.

Случайная величина, распределенная по нормальному закону с параметрами а=Ю и ст=і1, называется центрированной и норми­рованной нормальной величиной (часто ее называют нормирован­ной нормальной величиной). Если случайная величина х подчинена нормальному закону, то это обозначается так: x~N(a, а2). Укажем еще одно свойство нормального знакона. Пусть x~N (aXj a2i); Y—kX+b, где k и b — неслучайные коэффициенты, то. да Y~N (kcix + b, &%2i), т. е. линейная функция от аргумента, подчи­ненного нормальному закону, также подчинена нормальному закону.

Некоторые другие законы распределения. Распределения Стью — дента и хи-квадрат широко используются в теории надежности для построения доверительных интервалов параметров нормального распределения по выборке.

Гамма-распределение описывает время, необходимое для появ­ления. ровно т] независимых событий, если они происходят с посто­янной интенсивностью X. Это свойство обеспечивает широкое при­менение гамма-распределению. Отметим, что распределение хи-квад­рат — частный случай гаміма-іраспределения (при т)=я/2, где п — целое число, и Л=и1/2). Частными случаями гамма-распределения являются также закон Эрланга (при т|=|1, 2,…) и экспоненциаль­ное (показательное) распределение (при г) =11-). Экспоненциальное распределение наиболее широко используется для описания време­ни безотказной работы. Оно играет основную роль в теории надеж­ности подобно тому, как нормальное распределение играет основную роль в других областях.

Распределение Вейбулла часто принимается в качестве модели для времени безотказной работы .некоторых элементов, если интен­сивность их отказов изменяется во времени (см. гл. 4). Частным случаем распределения Вейбулла является распределение Релея (при а—2 и X— 1/о2), для которого интенсивность отказов — линей­но. возрастающая функция времени.

Логарифмически нормальное распределение описывает время безотказной работы некоторых элементов (например, транзисто­ров определенного типа). Р-распределение описывает распределение так называемого дисперсионного отношения, играющего роль при проверке статистических гипотез. Бета-распределение — основное распределение для случайных величин, ограниченных с обеих сто-
рои. Частным случаем бета-распределения является закон равно­мерной плотности (при а=Ь=її).

Усеченное нормальное распределение применяется для нормаль­но распределенных случайных величин с ограниченным диапазоном изменения и потому широко используется в различных приложе­ниях.

Дискретные распределения: биномиальное, Пуассона, геомет­рическое, отрицательное биномиальное часто используются в теории надежности, при статистическом контроле качества и в других технических приложениях.

Многомерные случайные величины. Состояние авиа­ционной системы обычно описывается несколькими чис­ловыми параметрами. Поэтому при изучении состояния авиационной техники приходится использовать матема­тические модели на основе многомерных случайных величин {Хь Х2,… , Хм). Как и одномерная, многомер­ная случайная величина {Кь . . . , Хм} полностью харак­теризуется своим законом распределения:

F(xu х2,…, Хм) =Р…, Хм<Схм). (1-4)

Только в одном частном случае, когда все составляю­щие Xk взаимно независимы, вместо многомерного рас­пределения (1.4) достаточно иметь М одномерных рас­пределений F(xu). Многомерная функция распределения содержит много больше информации, чем распределения всех составляющих вследствие того, что в ней ‘ дается описание взаимных влияний этих составляющих.

В частном случае многомерной нормальной случай­ной величины выражение (1.4) можно записать в явном виде:

Xdxь dx2,…. dxм,

где x={xi, х2,…, Хм) — вектор-строка размерности М; х= = {МХі, МХ2 МХм}—вектор математических ожиданий состав­

ляющих многомерной величины; 2 — матрица ковариаций, элементы которой подсчитываются по формуле аы—Cov(Xh, X;j=2(x4—

_ /

— MXi) (х%ь — MX к)] (х — х)’ — вектор, транспонированный отно­сительно вектора (х — х); 2-1 — матрица, обратная матрице 2; ]2| — определитель матрицы 2.

Как и в одномерном случае, многомерная нормально распределенная случайная величина описывается двумя матричными параметрами: К и Б.

Случайные процессы. Обобщением понятия много­мерной величины при М->оо является случайный про­цесс x(ti), наблюдаемый в дискретные моменты време­ни ti = iM при t= 1,2… Не вдаваясь в некоторые тео­ретико-множественные проблемы, можно считать, что так же определяется случайный ‘Процесс и с непрерыв­ным временем x(t). При эксплуатации авиационных систем даже непрерывные процессы изменения их пара­метров воспринимаются как дискретные, так как их измерение проводится через определенные интервалы времени At.

Хорошо согласующимися с практикой моделями слу­чайных процессов являются гауссовские процессы. Дей­ствительный случайный процесс £,(t) называется гаус­совским [21], если конечномерные распределения для значений £(£,) этого случайного процесса нормальны. Такой процесс полностью описывается математическим ожиданием рД)=М£(‘£) и корреляционной функцией R(t, s) =мш — ц(5)].

Изменением масштаба и сдвигом начала отсчета лю­бой гауссовский процесс можно привести к процессу с нулевым средним и постоянной по времени дисперсией §(^)=![х(<)—ц (;t)]lai{t). Такое приведение часто исклю­чает всю зависимость характеристик случайного процес­са от времени, т. е, позволяет рассматривать его как стационарный. Важный класс образуют стационарные процессы с рациональными спектральными плотностями

1 2 где р6, — постоянные коэффициенты; 0 — индекс суммиро­ вания, принимающий максимальные значения U и h X—перемен­ная частота.

Спектральная плотность f(X) имеет физический смысл средней энергии, приходящейся на составляющую с частотой % в разложении стационарного процесса на сумму гармонических колебаний. Функция }(%) одно­значно определяется через корреляционную функцию процесса I (t). Любую спектральную плотность процес­сов, наблюдаемых при эксплуатации авиационных сис­тем, можно как угодно точно аппроксимировать моделью

(1.5) . Эта модель имеет удобную интерпретацию при изучении процессов не через их спектр, а во временной Й’О

области. Дискретный процесс {t) со спектральной плотностью (1.5) при t=i№ подчиняется уравнению [13]:

Ь h

S Ре — в)At] =! 2 Pfo 6 — 0) ДА. (1 .б>

в=о е=о

где e[(i — 0)At] — случайный процесс с некоррелированными, значениями.

Процесс e{t) является в некотором смысле простейшим, случайным процессом, иногда его называют белым шумом. Такой процесс принимает независимые значе­ния при всех iAt и, следовательно, его значения непред­сказуемы.

Уравнение i(1.6) часто используют как математиче­скую модель изучаемых практических явлений. Коэф­фициенты li, l2, pj, в ней имеют физический смысл. Так, число 1 показывает, сколько рядом стоящих зна­чений процесса t,{iAt) связано между собой. Тесноту связи характеризует коэффициент авторегрессии рг0. Числа 12 и р0 —■ коэффициенты скользящего суммирова­ния показывают, сколько независимых белых шумоа принимают участие в формировании наблюдаемого про­цесса и как долго влияние каждого из них ощущается в наблюдениях g (/).

На модели (1.6) и в представлении (1.5) для /(X) молено проследить валшое свойство случайного процес­са, называемое марковским. Оно состоит в следующем: если точно известно состояние процесса в настоящий момент, то будущее состояние не зависит от прошлого, состояния. Иными словами, случайный процесс x(t) называется марковским, если для любых п моментов; времени tx<t2<. ,. . . , tn условная функция распределе­ния последнего значения x(tn) при фиксированных зна­чениях x(ti), x(t2) x(tn-1) зависит только от x{tn-і),.

т. e. при заданных значениях х, х2,, хп справедливо; соотношение:

P{x(tn)^XnJx(tl)=Xi, …. Ж (t„_,) =*„_,} =

= P{x(tn) S^Xnlxtfn-i) =Xn-i}.

Другими словами, процесс, задаваемый моделью (1,24), будет марковским, если равны нулю Р0 при ©>1 и при ©^1. Такой процесс иногда называют простым марковским процессом.

Однако понятие СОСТОЯНИЯ В ‘Момент времени ti мож­но расширить, считая, что оно описывается ‘многомерной характеристикой — значениями процесса в моменты ti-ъ ‘.при 0 = 0, 1, .. ., 1. Тогда марковское свойство следует понимать как независимость будущих состоя­ний от прошлых, имевших место При t^Lti — ш. Имен­но в таком расширенном понимании используется в .дальнейшем понятие «марковский процесс». Для него характерно равенство нулю всех i|3g при 0^1 в пред­ставлении (1.6) и запись спектральной плотности (1.5) ;в виде постоянной, деленной «а полином по степеням

Цепь Маркова. Если марковский случайный процесс может принимать конечное число состояний г = 1,2… F и переходы его из состояния в состояние осуществляют­ся в дискретные моменты времени, то говорят, что такой процесс r(ii) задает цепь Маркова. Полное вероятност­ное описание цепи Маркова состоит в задании совмест­ных вероятностей Р (г о, Г, . . . , г і) при разных І. Для вычисления их нужно знать начальное состояние (рас­пределение вероятностей Р(г0) пребывания в состоянии г в нулевой момент времени) и физический механизм смены состояний, определяющий вероятности qЦ (г0, Гр. ) перехода за р шагов (для всех O^p^t) из состоя­ния г0 в состояние Гр. Если изучается простая (т. е. с. зависимостью всего на один шаг) цепь Маркова, то

І

Р(Г0, П,…, /Д=Р(го) П ^(‘■р./Д-і^-

Н=1

Вероятности перехода за р шагов могут быть вычисле­ны последовательным перемножением вероятностей пе­рехода за один шаг q(r/s).

Цепь Маркова, для которой — вероятности перехода не зависят *от номера шага (остаются неизменными), называется однородной. .Для простой однородной цепи Маркова исчерпывающее вероятност­ное описание задается матрицей одношаговых вероятностей пере­хода {<7rs}, где qrs=q(r/s) — вероятность перехода за один шаг из •состояния г (г=<1, 2 ,…, F) в состояние s-(s=il, 2, …,Д). Дейст­вительно, в этом случае

{<7р. (ф)) = (дф».

Для ряда цепей Маркова при i-s-oo существуют предельные ■стационарные вероятности л (г) пребывания в г-и состоянии, неза­висимые от начального распределения Р(г0). Такие цепи называют

эргодичеокими. Финальные вероятности я; (г) могут быть определе­ны из системы уравнений:

F

я (г) =2 я (я)?™; г=л… F. (1.7).

.5=1

Система (1.7) обычно дополняется условием нормировки 2я(г) = 1^

г

так как из F уравнений (11.17) только (Я—>1) уравнений линейно- независимы.

Выборка. Исходным пунктом любого статистического исследо­вания случайной величины X является совокупность из п наблюде­ний, в результате которых величина X принимает значения х^ Х2 Хп.

Впоследствии предполагается, что опыты (испытания), в резуль­тате которых случайная величина принимает определенные значе­ния, являются взаимно независимыми и производятся в неизмен­ных условиях.

Значения xi, Х2,…, х„ называются выборкой из генеральной; совокупности или иросто выборкой, каждое отдельное значение­м-элементом. выборки (t=lL, 2,…, и), а общее количество эле­ментов п — объемом выборки.

Предполагается, что число членов N в генеральной совокупно­сти велико, а объем выборки п ограничен. При достаточно большом N свойства выборочных (статистических) распределений и харак­теристик практически не зависят от N. Отсюда вытекает математи­ческая идеализация; состоящая в том, что генеральная совокуп­ность считается бесконечной. При этом отличают точные характе­ристики (закон распределения, математическое ожидание, диспер­сию и другие моменты), относящиеся к генеральной совокупности,, от аналогичных им выборочных (статистических) характеристик, (статистических оценок). Выборочные характеристики отличаются от соответствующих характеристик генеральной совокупности вслед­ствие ограниченности объема выборки п. При неограниченном уве­личении п все выборочные характеристики приближаются (сходят­ся по вероятности) к соответствующим характеристикам генераль­ной совокупности. Выборочные характеристики в отличие от харак­теристик генеральной совокупности — случайные величины.

Опытное распределение и его числовые характеристики. Выбор­ку иногда называют простой статистической совокупностью или простым статистическим рядом. При большом1 числе наблюдений; (более 30]) простая статистическая совокупность неудобна для. записи статистического материала: запись становится слишком гро­моздкой и малонаглядной. Поэтому на основе простой статистиче­ской совокупности строится так называемый статистический (сгруп­пированный) ряд. Весь диапазон наблюденных значений случайной величины делится на интервалы (разряды), и подсчитывается час­тота (количество) значений случайной величины ГПі, приходящихсяі на каждый 1-й интервал.

Отношение частоты т, к общему числу наблюдений п назы­вается частостью (относительной частотой), соответствующей дан­ному разряду: р,=т(/п. Очевидно, что сумма частостей всех интер­валов равняется единице.

Число интервалов, в которые следует сгруппировать статистиче­ский материал, не должно быть слишком большим, так как при; большом числе интервалов ряд распределения становится яевыра-

зительным и частоты в нем’ имеют незакономерные колебания. Но число интервалов не должно быть слишком малым, тогда свойства распределения описываются рядом слишком грубо. Группировка в 10—20 интервалов, в каждый из которых попадает не более 15—

20 % значений случайной величины, обычно оказывается достаточ­ной для полного выявления всех существенных свойств распределе­ния и надежного вычисления основных числовых характеристик — слу­чайной величины.

Статистический ряд часто изображается графически в виде ги­стограммы, которая строится следующим образом. По оси абсцисс откладываются значения интервалов. На каждом из интервалов стро­ится прямоугольник, площадь которого равна частости данного *■ интервала. Для этого частость каждого интервала необходимо раз­делить на ширину интервала и полученное число взять в качестве высоты прямоугольника. В случае равных по ширине интервалов высоты прямоугольника пропорциональны соответствующим часто­стям.

Из способа построения гистограммы следует, что полная пло­щадь гистограммы равна единице.

Выборка Хі, Хг,…, хп может быть описана функцией распре­деления или числовыми характеристиками, которые в этом случае ■называются статистическими или выборочными. Любой характери­стике генеральной совокупности может быть поставлена в соот­ветствие статистическая характеристика. Функции распределения F(x) соответствует статистическая функция раопределения F*(x)

(другие названия: выборочная функция. распределения, эксперимен­тальная функция распределения, функция опытного распределения), -плотности вероятности f(x) — гистограмма, моментам распределе­ния as и ps — статистические (выборочные) моменты as и tns-

Статистическая функция раопределения любой случайной вели­чины (дискретной или непрерывной) представляет собой ступенча­тую функцию, скачки которой соответствуют экспериментальным значениям случайной величины и равны частостям этих значений.

Если каждое отдельное значение случайной — величины X встрети­лось.1-. раз, то все скачки F*(x) равны 1 /я.

Статистические (выборочные) начальные и центральные момен­ты опытного распределения определяются соответственно следую­щим образом:

, " , « _

asm= _L 2 ms[X= — 2 (*; — х)‘,

п (=i п г=і

_______ п

где х=аіИ=’2хі/я — среднее арифметическое эксперименталь — i=i

ных значений.

Для статистических моментов справедливы те лее свойства, что ■и для моментов теоретического распределения. Наибольшее значе­ние для оценки опытного раопределения (так же, как ранее для теоретического) имеют, первый начальный момент (выборочное вреднее или просто среднее) и второй центральный момент (выбо­рочная диоперсия) —

В заключение этого вводного раздела по математической ста­тистике укансем на несколько значений термина, «статистика».

Прежде — всего статистика есть одна из научных дисциплин, изучаю­щая данные, .полученные исчислением или измерением свойств гене­ральных совокупностей явлений материального мира. В этом смысле различают статистику социальную, экономическую, математическую и др. Тем же словом «статистика» называют совокупность числовых данных о каком-либо явлении или процессе, и в этом смысле ста­тистика означает множество данных (напомним часто употребляю­щееся словосочетание «набрать статистику»). В этих двух смыслах «статистика» употребляется только в единственном числе. Есть и еще одно значение термина «статистика» — так называют функцию от элементов выборки из некоторой генеральной совокупности. В этом омысле «статистика» употребляется как в единственном, так и во множественном числе.

В дальнейшем слово статистика будет употребляться именно в этом смысле.

Выбор вида закона распределения. Подгонка закона распределения случайной величины на основе опытных данных, т. е. по выборке, включает три этапа: выбор

предполагаемого вида закона — распределения; проверку согласия выборки с принятым законом распределения, т. е. согласованности опытного распределения с теорети­ческим; оценку параметров выбранного закона распре­деления.

Подбор для данного статистического ряда теорети­ческой кривой распределения и нахождение ее парамет­ров в статистике часто называют выравниванием (сгла­живанием) статистических рядов. Основой выравнива­ния является выбор вида теоретической кривой распре­деления. Главное в выборе вида теоретического распре­деления — это понимание характера рассматриваемого явления. Другими словами, вид теоретического распре­деления, как правило, должен выбираться заранее из соображений, связанных с существом рассматриваемого явления. Бели нет веских соображений в пользу какого — либо теоретического распределения, то можно восполь­зоваться следующим приближенным способом. По опыт­ным данным находят оценки коэффициентов асимметрии gi и эксцесса g2′

gi=m3/(/пн)3′, g2=mjm22 — З, (1.8)

Точку с координатами (g2i, g2) наносят на график (рис. 1.1). Бели эта точка будет лежать достаточно близко от точки, прямой или области, соответствующих определенным теоретическим распределениям, то это распределение может быть использовано для описания опытного распределения. Следует заметить, что данный

Рис. її Л. Области, соответству-
ющие разным типам распреде-
лений в зависимости от асим-
метрии эксцесса:

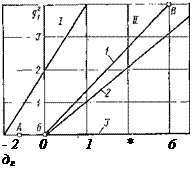Л —закол >р&1вламефлой плотности; Б—-нормальный закон; В — экспо — •ненщиаль’ный закон; I — критиче­ская область ; II — бета-раагвреде — ление;

1 — ігаїміма-раюп. ределен’ие; 2 — лога-
рифмически. нормальный закон; 3 —
•распределение Стьюдента

способ не гарантирует правильности выбора — вида тео­ретического распределения, поскольку форма кривой распределения не определяется однозначно коэффициен­тами асимметрии и эксцесса, да и вместо последних в формулах (1.8) используются их оценки.

Опытное распределение часто можно аппроксимиро­вать одинаково хорошо разными теоретическими распре­делениями. .Критическая область представляет такие сочетания g2i и g2, при которых невозможно существо­вание закона распределения. Нормальный закон рас­пределения, закон равномерной плотности и экспонен­циальной представлены на графике одной точкой, по­скольку они не имеют параметра формы и вследствие этого всегда имеют единственную форму. Гамма-распре­деление, логарифмически-нормальное распределение и закон Стьюдента представлены прямыми, так как они имеют по одному параметру формы. Бета-распределе­ние, имеющее два параметра формы, занимает на гра­фике определенную область. После выбора тем или иным способом теоретического распределения возникает задача нахождения оценок неизвестных параметров за­кона распределения. Оценкой параметра называется его значение, найденное по ограниченному числу наблюде­ний (по выборке). Существуют несколько методов по­лучения оценок неизвестных параметров 0 закона рас­пределения Генеральной СОВОКУПНОСТИ ПО Выборке Х, х2,. . ., хп. Наиболее распространены из них метод мо­ментов и метод максимального правдоподобия.

Этот метод требует применения предварительного предположения о виде закона распределения, который считается известным, кроме значений параметров 0, входящих в аналитическое выражение этого закона. 26

В соответствии с методом максимального правдоподобия следует построить функцию правдоподобия £(0), зави­сящую только от неизвестных параметров ©, и найти значения 0, при которых функция L(0) обращается в, максимум. Найденные значения 0 и принимают в каче­стве оценок параметров распределения.

■В качестве оценки математического ожидания а (ге­нерального среднего) используется среднее выбороч­ное х:

Для нормального закона распределение оценки х является нормальным N (а, а2/п) независимо от объема, выборки.

В качестве оценки дисперсии а2 генеральной сово­купности обычно используют две оценки (в случае неиз­вестного генерального среднего): выборочная диспер — 1 п —

сия 2 =— V (х; — л)2; несмещенная оценка дисперсии « іГі

— —- ‘}) (х,—xf. При известном генеральном среднем.

n~h=i

а несмещенная оценка дисперсии о2 находится по фор­муле S2о = — (** — аУ-

п jti

Проверка статистических гипотез. Статистической: гипотезой называют любое предположение относитель­но свойств генеральных совокупностей, сделанное на. основании выборок из этих совокупностей. Практически, большей частью эти предположения сводятся к некото­рым утверждениям относительно параметров закона, распределения. Возможны и другие гипотезы, например,, о равенстве параметров двух или нескольких распреде­лений, независимости выборок, возрастании интенсив­ности отказов и т. д.

Проверка статистической гипотезы заключается в вы­боре решения: принять гипотезу или отвергнуть ее.. Принятие решения обычно основывается на выбороч­ных характеристиках, которые в этом случае называют­ся критериями (статистиками) для проверки статисти­ческой гипотезы. Критерии статистической гипотезы В; силу того, что они являются выборочными характери-

тг

стиками, представляют собой случайные величины, за­коны распределения которых в общем случае определя­ются законами распределения генеральной совокупно­сти и объемом выборки п. Числовое значение критериев полностью определяется выборкой.

Проверяемую гипотезу называют нулевой, а противо­речащую ей — альтернативной гипотезой. Нулевую ги­потезу обычно обозначают Н0, альтернативные гипоте­зы — Н, #2 и т. д. Если нулевая гипотеза отвергается, то это одновременно означает, что принимается альтер­нативная гипотеза. При проверке статистической гипо­тезы возможны следующие случаи: гипотеза Я0 верна и принимается; гипотеза Я0 неверна и отвергается; гипо­теза Я0 верна, но отвергается; гипотеза Я0 неверна, но принимается. Таким образом, при проверке гипотезы возможны ошибки двух типов. Разница между указан­ными ошибками весьма существенна вследствие того, что различна значимость этих ошибок.

Ошибку, заключающуюся в неоправданном отклоне­нии верной проверяемой гипотезы, называют ошибкой 1-го рода. Ошибку, заключающуюся в принятии невер­ной проверяемой гипотезы, называют ошибкой 2-го ро­да. Обычно вероятность ошибки 1-го рода (эту вероят­ность называют уровнем значимости) обозначают через а, а вероятность ошибки 2-го рода — через р.

Естественно желание сделать так, чтобы вероятности ошибок а и іР при проверке гипотез были как можно меньше. Однако при фиксированном объеме выборки п это сделать невозможно. За уменьшение уровня значи­мости приходится «расплачиваться» увеличением веро­ятности ошибки 2-го рода и наоборот. В связи с этим сначала назначают уровень значимости а (обычно 0,01 — 0,1), а затем выбирают такую процедуру проверки, ко­торая обеспечивает минимальное значение р. Единст­венный способ одновременного уменьшения вероятно­стей ошибок аир — увеличение объема выборки п.

Процедура проверки статистической гипотезы заклю­чается в сравнении вычисленного по выборке критерия с возможными значениями критерия для проверяемой гипотезы. Важнейшей принципиальной особенностью проверки статистических гипотез является то, что в ре­зультате проверки нельзя доказать ни одной гипотезы. Проверяемая гипотеза или отвергается, как явно несов­местимая с опытными данными, или принимается. Од­

нако принятие гипотезы ни в коем случае не может считаться доказательством ее справедливости. Оно озна­чает только то, что гипотеза не противоречит опытным данным.

Проверка согласия опытного распределения с теоре­тическим. Пусть опытное распределение, заданное вы­боркой объемом п, выравнено с помощью некоторой тео­ретической кривой f (x). Однако между теоретической кривой и опытным распределением неизбежны расхож­дения. Следует выяснить, объясняются ли они только случайными обстоятельствами, вызванными ограничен­ным числом наблюдений п, или они существенны и свя­заны с тем, что подобранная теоретическая кривая пло­хо выравнивает данное опытное распределение. Для от­вета на такой вопрос служат так называемые «критерии согласия».

В качестве критериев согласия в статистической практике обычно применяют критерии Колмогорова, %2, со2 и некоторые другие. Приведем в качестве примера один из них.

Критерий %2 основан на том, что величина

Г

X2=S (Wt — npi)2/npu (1.9)

где pi — теоретическая вероятность попадания случайной вели­чины в і-ц. интервал; при п->-оо асимптотически подчинена распре­делению %2 с числом степеней свободы г — 1.

Критерий %2 может применяться для проверки любо­го теоретического распределения, при этом результаты наблюдений обязательно должны быть сгруппированы в интервалы.

Проверка нормальности распределения. Гипотезу о нормальности распределения можно проверить с по­мощью многих статистических критериев, в том числе и рассмотренных критериев Колмогорова, %2 и ш2. Од­нако для приближенной проверки можно использовать свойство нормального распределения, заключающееся в том, что для него коэффициенты асимметрии и эксцес­са равны нулю.

Случайными (не систематические или статистически незначимые) отклонениями от нуля можно считать лишь те значения выборочных коэффициентов асимметрии и эксцесса, которые не превышают 1,5—2 средних квадра­тических отклонений соответствующего выборочного

коэффициента. Нормальность распределения проверяют следующим образом.

1.Определяют выборочный коэффициент асимметрии gi и выборочный коэффициент эксцесса g2 по форму­лам (1.8).

2.Определяют средние квадратические отклонения выборочных коэффициентов асимметрии и эксцесса:

s I / &(п — 6) . = 1 / ’24га(я—2) (л—3)

V (я+11)-(я+0) ’ Si V (я-Н1)а(л-МЗ)(я+5)

(1 10)

3.

При выполнении одновременно неравенств

можно считать, что опытные данные не противоречат нормальному распределению.

Если же выполняется хотя бы одно из неравенств

то предположение о нормальности распределения следу­ет отвергнуть. Если l,5Sg]< |gi | <25^; l,5Sg2< 1^2 +

<2Sgs, то необходимо провести дополнительную

проверку с помощью каких-либо других критериев. Проверка гипотез о средних. Два выборочных сред­

них сравнивают в случае, — когда имеются две незави­симые выборки объемом П и «2 из нормально распреде­ленных генеральных совокупностей. При этом по выбо­рочным средним Xi и х2 проверяют гипотезу: равны ли генеральные средние рі = рг — Вид критерия проверки гипотез зависит от того, известны ли заранее дисперсии или нет, а также от того, равны они или неравны. Уро­вень значимости а считается заданным. Например, если дисперсии известны, то проверка гипотезы Я0: pi = p2> Я і.: р, і=?Ні2 проводятся следующим образом.

Вычисляют значение критерия

С*1 — Х2) V «1«2 — — •

V Я2021+Я1022

Гипотеза Я0 принимается, если |u|<«i-a/2, отверга­ется, , есліг I и] > «1-0/2.

Проверка гипотез о дисперсиях. Одной из важней­ших задач статистической обработки опытных данных является проверка гипотез о дисперсиях. Рассмотрим гипотезы, основанные на сравнении двух выборочных дисперсий о21 и <т22- Предполагается, что генеральная совокупность распределена по нормальному закону.

Сравнение двух выборочных дисперсий проводят в случае, если имеются независимые выборки объемом п и п2 из нормально распределенных генеральных сово­купностей. В общем случае гипотезу можно сформули­ровать следующим образом: Н0: cr2i/a22=i&, где к— за­данное число. Здесь для простоты рассматривается случай, когда k=.

Проверку выполняют следующим образом.

1. Вычисляют отношение

F=sys. (4.12)

В качестве S2i берут большую из сравниваемых оценок дисперсии.

2. Из таблиц для F-распределения находят квантиль

; л,—1, г2-1 ■

2

Гипотеза #0 принимается, если Fs^Fх_ „,_i; „„_i,

2

и отвергается, если F>Fі_ 1_; Лі_і; /Ia_i.

2

На рассмотренных приемах проверки гипотез бази­руется методика анализа надежности авиационной тех­ники, излагаемая в дальнейшем.

Во многих прикладных задачах для проверки выдви­гаемых гипотез по исходным данным ограниченного объема используют статистики, основанные на %2-рас- пределении. Тесты такого типа применяются, в частно­сти, в данной книге при оценке структуры случайных последовательностей по полученным экспериментально их реализациям и при анализе наборов цифровых пока­зателей методами многомерной математической стати­стики. При этом считается, что распределение наблю­даемых случайных величин, относительно которых про­веряются выдвигаемые гипотезы, нормальное.

Практически предположение о нормальности не сни­жает общности решения, так как оно обычно подтверж­дается вескими интуитивными соображениями или ста­тистической проверкой. Тем не менее оценка ошибки, которую вносит это начальное предположение, пред-

ставляет немалый интерес, так как — с сомнениями отно­сительно устойчивости к изменениям вида распределе­ния исходных данных (крепости) теста типа %2 часто бывают связаны возражения по его применению во мно­гих конкретных приложениях. Известно, что тесты на основе х2 не очень мощные. Иными словами, чтобы ве­роятность ip2 отвергнуть проверяемую гипотезу, если она неверна, была значительна, необходимо, чтобы постро­енная для проверки данной гипотезы статистика и была заметно меньше (на 6х) границы х2 (“. п) ■

Граница х2 (<х, я) выбирается из условия малости вероятности (її = а отвергнуть проверяемую гипотезу, если она верна. По таблицам нецентрального распреде­ления х2 можно оценить мощность теста, построенного на основании статистики и, и указать такие отклонения бх от граничного значения х2 (а, я), которые обеспечат вероятность отвергнуть неверную гипотезу не ниже за­данной. Удовлетворительную уверенность при принятии проверяемой гипотезы удается получить, если контроль­ная статистика и на 30—40 % меньше, чем граничное значение х2 (а, я) при а=5 %.

Если несправедливость начального предположения о нормальности наблюдаемых случайных чисел приве­дет к изменению статистики и менее чем на 6х=30-Е 4-40 %, то можно полагать тест на основе х2 «крепким», так как на окончательном решении о принятии прове­ряемой гипотезы распределение х не скажется. Провер­ка крепости теста х2 путем прямого численного экспери­мента на цифровых вычислительных машинах позволя­ет считать, что статистика и слабо меняется при изме­нениях начального распределения. Даже для таких рас­пределений, как экспоненциальное и логарифмически нормальное, тест типа х2 применять можно, хотя эксцесс и асимметрия этих распределений весьма значительны.

Некоторое представление о деформации распределе­ния статистики типа х2 при применении ее к негауссов­ским распределениям помогает получить проводимое в дальнейшем аналитическое исследование [22],

Случайная величина и, распределенная по х2 с 11 степенями свободы, получается при суммировании квад­ратов я независимых случайных чисел с нормальным распределением f(x), нулевым математическим ожида­нием М[х] = 0 и единичной дисперсией D[x] = сг2 = 1. Если производить суммирование квадратов я центрирован­

ных и нормированных (M[x] = 0, D[x] = 1) случайных чисел с произвольным распределением р{х), то получим

П

число н=2х2г с некоторым распределением р{и). От — і=і

личие р(и) от ^-распределения р[%2(и, п)] будет опре­деляться моментами (ВЫСШИХ порядков Цз, Ц4, . .. исход­ного распределения р{х).

Можно показать [22], что

И 21 f a. l k

Ж=Р[хН«, п)] 2 2 С"А f П —— ■ (.1.13)

1=0 к — о V 8 / у=і п+2і;

В выражении (1.13) второй сомножитель характери­зует влияние эксцесса £г исходного распределения на вид плотности распределения статистики и. На рис. 1.2 приводится характер поправки h=p (и)/р>[%2 (и, п) ] в за­висимости от числа степеней свободы п и величины экс­цесса. Сплошные ЛИНИН соответствуют значениям £2 = 2, а штриховые — £2 = 4. Нечетные моменты распределе­ния р{х), в частности коэффициент асимметрии, ника­кого влияния на распределение статистики и не оказы­вают.

Практический интерес представляет вид плотности распределения статистики и для тех значений и, при ко­торых р(и) заметно отличается от нуля. Первый со­множитель в (1.13) отличен от нуля при М[уР — — 1,бУД%2]<ц<М[%2]+ 1,буН[х2]. Именно для таких и.

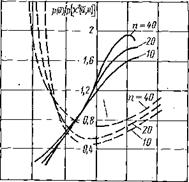Рис. 1..2. Поправка к плотности
распределения суммы квадра-
тов независимых случайных
величин

Т>(Щ

~2ft -16 -0,8 0 0,8 1,6 и

■ ‘ й

на рис. 1.2 дается значение отношения распределения р(и) к р[%2{и, и)]. По оси абсцисс откладывается значе­ние аргумента и в относительных единицах: и=

= (ц-ми)7№1

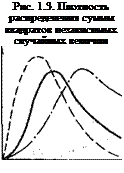
На рис. 1.3 показана деформация распределения суммы квадратов независимых случайных величин: сплошной линией — плотность распределения %2> штри­ховой вид р (и) для случайных величин х с плосковер — шинным распределением (^2>0), а штрихпунктирной — вид р(и) в случае, если распределение р(х) островер­шинное (g2<0). Для концентрированных (плосковер­шинных) распределений изменение р (и) относительно р[%2(и, п)] не может быть большим, так как ^/8^0,25. Это позволяет надеяться, что в большинстве практиче­ски интересных случаев отличие р(и) от p'[%2(w, я)] бу- дует невелико, так как в реальных экспериментах редко встречается такой разброс результатов, чтобы за пре­делами M{x]±2PjDx лежало больше 0,3 % опытных данных.

Для островершинных распределений деформация р(и) относительно р[%2(и, п)] может быть гораздо более существенной при большом эксцессе распределения р (х). Однако в этом случае деформация р (и) такова, что применение к статистике квантилей %2(а, п) будет только ужесточать критерий. При а=5 % слева от %2( а, п) в случае справедливости гипотезы М[х = 0 бу­дет лежать более 95 % значений и, если g%>0.

Таким образом, для большинства практических задач критерий типа х2 оказывается мало чувствительным к отклонениям исходных распределений от’ нормального.