ОПРЕДЕЛЕНИЕ СИЛ И МОМЕНТОВ НЕСУЩЕГО ВИНТА

Найдем проекции элементарных сил лопасти, которые определены в разд. 1.2.2, на полусвязанные оси несущего винта 0HXHYHZH. На рис. 1.14 показаны проекции лопасти на плоскость вращения несущего винта (на плоскость 0HXHZH) и вид на лопасть спереди (по стрелке А). Из рис. 1.14, а видно, что проекции элементарной тяги dtn на оси ОиХи, Он Ун, OnZH соответственно равны dtn sin j3n cos фп dtn cos(Зл ; — dtn sin (Зл sin фп. Соответственно проекции силы dqn и силы трения dfn : dqn sin фп ; 0; — dqn cos фп ; — dfn cos0n cos фл ; dfn sin (Зл ; dfn cos/Jjj sin фл.

Просуммировав проекции сил, направленных по оси ОнХк, найдем элементарную продольную силу несущего винта

dhH = — dtn sin /?л cos і/’д + й?<7л sin + <//л cos /?л cos і£л. (1.71)

Аналогично найдем элементарную тягу и боковую силу несущего винта:

dtH = dtn cosff„ + df„ sin j3n ; (1.72)

<*h = — dtn sin 0n sin іl/n — dqn cos фл + dfn cos sin фп. (1.73)

Проинтегрировав выражения (1.72) … (1-74) по радиусу лопасти, найдем мгновенные значения ее сил; обозначать их будем верхним индек­сом ф.

і і

ht = fdhH = f ( — dtn sin cos фл + sin фп + о о

+ dfn cos0n cos ^л) = — t% sinPn cos фл + q%sin ф„ +

+ . , (1-74)

+ cos (Зл cos фп;

4 = /*„; 4 = /*„•

о 0

Средние значения коэффициентов сил винта равны

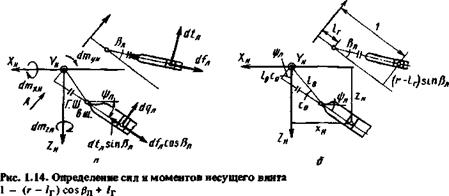2л о 2л о

1 2JT

sH = — / 4<^Л‘

2іг о

Элементарные инерционные силы лопастей после интегрирования по площади несущего винта равны нулю, так что выражения (1.75) явля­ются окончательными выражениями для коэффициентов сил несущего винта. Переход к размерным значениям сил лопасти осуществляется пу­тем умножения коэффициентов на p(ooHR)2 bR/2 = р(сои7?)2 oF/2kn, а сил несущего винта — на p(u>HR)2 oF/ 2.

Элементарные моменты аэродинамических сил относительно полу — связанных осей несущего винта

dmXH = — dtH zH + dsHJH; dmyH = ~dsHxH — dh~zH -,

— — (1-76)

dmZH = dhHyH + dtHxH.

Выражения для координат элемента лопасти получим с помощью рис. 1.14, б:

хн = ?г)со^л + lr]cos^n + /в со sin Фп

Ун = (r — lr)sin 0л; С1-77)

2н = [O’ — *г)СО!50л + 1г^пК + *BcoCOS^n.

Подставим в (1.76) формулы (1.71) … (1.73), т. е. перейдем к эле­ментарным силам лопасти:

dmXH = — dtn[(r — /г + 7Г cos 0Л) sin фл + Тв с0 cos /Зл cos ^л] —

— dqn(F — /г) sin 0П cos ^л — dfn sin/Зп(/Г sin фл +

+ 7Bc0 cosi^); (1.78)

^ткн = = <*7лК’~ 7r)cos0n + /г)] +

+ (dfncos$n — dtn sin 0n) 7B c0 ; (1.79)

cfmZH = — dtn[(r — 7Г + /г cos 0Л) cos і£л — 7B c0 cos 0Л sin^ ] +

+ dqn(r — /г)8іп0п8іп^л — й?/л sin /Зл (7r cos v!/n —

— lBc0sinpn). (1.80)

Выражения (1.78) … (1.80) получены формально. Проследим с по­мощью рис. 1.15 происхождение каждого слагаемого этих выражений. На рис. 1.15, а показаны две проекции лопасти, находящейся в азимуталь­ном положении фл = 90°. Из вида на лопасть спереди (по Л) следует, что dmXH = — dtn{r — /г +_/г cos /Зл) — dfn 7Г sin /?л, а сила создает моменты: dmZH = dqn(F- /r)sin/3„, = -dqn[(r — /г)cos0n + /г].

Так как лопасть находится перед плоскостью Ои УНЛН (левая часть

рис. 1.15, а), возникают моменты dmyH = (dtn sin(Зл — dfn cosРл)Івс0; dmZH = (dtn cos|3n + dfn sin /Зл)/в c0 . Сопоставив полученные выражения и выражения (1.78) … (1.80) при sin фл = 1, соїфп = 0, видим, что они совпадают. Аналогично на рис. 1.15, б показаны проекции лопасти в ази­мутальном положении фп — 0. Из рис. следует, что

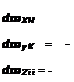
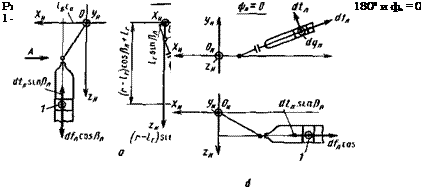
dqn (Г — /г) sin /Зл ;

dqn [(7 — /”r)cos0n + Тту,

dtn(r — /г + / г cos (Зл ) — dfn Tr sin Рл.

Из проекции_ на плоскость вращения видно: dmXH = -(dtII cos 0Л + + dfn sin(Зл)/в с0 ; dmyjl = (dtn sin /Зл dfn cos/Jj,) /в c0.Все эти слагаемые также совпадают с выражениями (1.78) … (1.80) при sin фл = 0, cos ф^~ 1.

Выражения (1.78) … (1.80) могут быть использованы для вычисле­ния моментов несущего винта, но их можно преобразовать іак, ЧЮбы получить формулы для определения средних моментов тхн , т, н щ ко­нечном виде. Для сокращения формул пренебрежем слагаемыми, Содер­жащими малые величины dfn, dсоH/d фл, g, с о (но произведение с0 в выражении (1.82) велико), а также примем, что угол j3„ мал. Тогда

dmxn = — (dtn + $ул)-7*тфл — №л — d/xn)(r — 7 )0п cosфл

~ djzn /г Рп sin Фл ; (1.81)

dm к» = (dqn — djxn)T + djznlBc0; (1.821

dmZil (dtft + djу л ) г cos + (dQn djXy ) ( f lr ) Pn sin фл

— djzn Tr 0jj cos фл. (1.83)

Возьмем интеграл по радиусу от dmXK, используя равенство (1.82):

тІн = “ / (Г — rr)sin фп (dta + ) — Гг(/* + /*,)sin фп —

— шкн cos + Гр (<7* — /*П)0Л cos — /*Л7Г Лл sin ф„ =

= + і%л + ЦпЫ’Ы’я ~ [«Sh — — /*„)]0nCOS«V

(1.84)

Интеграл в правой части (1.84) равен нулю, так как он выражает условие равенства моментов всех сил относительно оси горизонтального шарнира. При принятых нами допущениях j£n = 0 и инерционные силы в выражении (1.84) приводятся к виду (см. формулы (1.43) … (1.45))

-Щп + /£А)Гг*іп К = [So 0л + Sv~h —

— 250(c3XHcos фл — со2н sin фл ) — So 0„ ]Tr sin фл. (1-85)

Сокращение слагаемых 5о0л в правой части (1.85) соответствует тому, что центробежная сила лопасти, приведенная в горизонтальный шарнир, не создает момента, так как находится в плоскости вращения. Представим коэффициенты в виде гармонических рядов. На­пример: л

= *п + Wcos^ + іл1$йпфл + /Л2С cos2^n + … (1.86)

При этом уравнение (1.84) можно проинтегрировать по азимуту. Так как < ш^н, получим

1 — — _ — 1

тхи ~ ~r(Sr^i — ^ли + 25o<oZH)/r + wKHiceo).

2 2 (1.87)

С учетом поворота лопасти относительно вертикального шарнира формула (1.87) и аналогичная формула для тш примут вид

тхтл ~ l(Sr6i — tnU + 25ou»ZH)/r + mKHai —

~ ткнісао — (^nic + ^So ojxi1)]/2; (1.88)

mZK ~ I(Srei — *ліс — 25o wXH) lr — Мусн^і

+ ткяиао (^nis — ^So co2H)/вCo]/2. (1.89)

В формулах учитывают, что при |3Л =£0 лопасти не находятся в плос­кости вращения, так что. создаются моменты силами dqn (слагаемые, содержащие тки). Другое обстоятельство, учтенное в формулах (1.88), (1.89), — отклонение лопасти вокруг вертикального шарнира, из-за чего возникают моменты на плече /вСо — Формулы показывают, что у винта без выноса горизонтальных шарниров моменты тхи и тги не равны нулю и изменение параметров продольного движения (аг, 6В, согн) изме­няет не только т2н, но и тхи, и наоборот. Это значит, что возникают так называемые перекрестные моменты, которые нужно учитывать при выборе кинематических параметров втулки несущего винта, в расчетах динамики полета.

В выражения (1.88), (1.89) входят гармоники тяги и крутящего мо­мента, определение которых затруднено. Поэтому часто используются неполные формулы:

mXH	= (Srlrbl +	2So ь>2и1г + mKHai)/2;
	— —	_ _	(1.90)
	= (STlTax —	2Sb03XnlT — 2;
mXH	= Vr*i/2;	^ZH $r ^rai/2*	(1.91)

Формула (1.90) для т2и достаточно точна, но тхн определяется с большой ошибкой. Формула (1.91) для т2и дает заметную погреш­ность при больших 50 на срывных режимах. Некоторые авторы выводят формулы для тхн, т2и в предположении, что равнодействующая всех сил лопасти равна центробежной (что практически правильно) и направ­лена по оси лопасти (что неправильно]^; при этом получаются формулы (1.91), но вместо Sг в них входит S0. Приведем выражение (189) к размерному виду:

Мги ~ [ын I2 — S0 toH (<о2н/г + ^хн^в^о)] —

— (wkh^i — ^кнії^о + (піс^г — t^l^poFR^RfH.

Инерционные составляющие момента ЛГгн, а также Мхн не зависят от р, а действительно безразмерным является последний многочлен (в скобках).

Крутящий момент несущего винта от аэродинамических сил тк н а находится интегрированием выражения (1.79). Без учета меньших по ве­личине слагаемых получим

_ 1 27Г j _

*»k н. а — dqnr, тк н а — / dфп J dqnr. (1.92)

2іг о о

Для определения инерционной составляющей крутящего момента нужно в выражении (1.79) заменить dqn на — djхл, dtn на djyn, dfn на djZJi. С некоторыми допущениями (угол (Зл мал, djVJ10 <dj2Л, g = = db>Jdtn= 0)

^тк н. ин Фxjr + djzn iB Cq ;

fflK И. ИН ~ “ (^Г + ) (а1 Ы7Н + Ш7н)’

Таким образом.

1 2Л 1 _

ткн — тк н. а тк н. ин = f f dqл г —

2-п о о

~ (Тг + 5г7г)(а, WZH + Ьій)хн). (1.94)

В формулах для определения моментов несущего винта составляю­щие, содержащие аэродинамические и инерционные моменты, получают­ся разными при разных способах вывода формул. В разд. 1.3 выражение для тк н преобразовано так, чтобы использовать условие равенства нулю момента относительно оси вертикального шарнира; при этом полу­чили выражение (1.52) для крутящего момента от инерционных сил,

|_ 21Г 1

а момент от аэродинамических сил -2- f йфл f дя

2п о о

эти составляющие выражены иначе. Разница получается оттого, что при использовании условия равенства нулю моментов относительно оси шар­нира аэродинамические силы частично заменяются равными им инерци­онными.

При выводе формулы (1.84) для тхн силы, параллельные оси Оп Ул, переносили на ось горизонтального шарнира, после чего находили их мо­менты. При этом момент инерционных сил выражался формулой (1.85). Получим выражения для тш ин, шгн ин без переноса сил на ось шар­нира. В соответствии с (1.81), (1.43) … (1.45)

__ — upn

2(r — /г) —— (ь»хясо* фл —

d*n

cjzh sin і^л ^л)(/" ) 0л cos [(^ + 2т /1Л (сохн cos фл —

d(3n

— coZHsin і//л) — 2(г — /г) —— (coXHsin ф +

d*n

+ w2Hcos ^n)]/r|3nsin фл I. (1.95)

Отбросим слагаемые порядка малости (Зл и выше:

_______ — d20

йтхн. ин = <*тл [г(г — /г)(——5- + Рл) —

d*n

— 2г2(йхн cos фл — wZH sin фл)] sin фл. (1.96)

Проинтегрировав по площади винта, получим формулу для тхи ин и аналогично для т2л ин :

тхн. ин = Ло > тгн. ин = ^и> шхн ■ (1-97)

Таким образом, в прямолинейном полете средний инерционный момент равен нулю, а в криволинейном полете он создается направленными вдоль оси Он YH кориолисовыми силами, т. е. представляет собой гироскопи­ческий момент.

Также, без переноса сил на ось горизонтального шарнира, можно полу­чить другие выражения для аэродинамических составляющих моментов лгхна, т2н. а — При обоих способах вывода формул суммарное значение моментов одинаково.

При выполнении маневров гироскопический момент винта может достичь большой величины, но при этом обязательно будет таким же боль­шим и противоположного знака момент от аэродинамических сил (см. формулы (1.78), (1.80)). Поэтому суммарный момент винта существен­но меньше гироскопического.