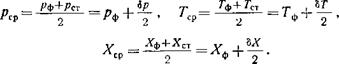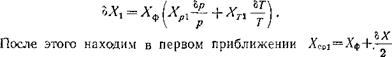МЕТОД ДИФФЕРЕНЦИАЛЬНЫХ ПОПРАВОК

Пусть подлежащая приведению летная характеристика X за­висит от давления воздуха р и температуры его Т:

Х=/(Р, П (6.5)

Продифференцируем обе части равенства (6. 5):

dX= — dp + — dT, (6.6)

дрн дТ у ‘

разделив на X, после преобразований получим

dX___ р дХ dp. Т. дХ dT (6 6′)

Х~Хдрр + Хд1Т’ К ‘ >

dX

где ——- так называемый логарифмический

X

р ен ци а л.

Безразмерные коэффициенты вида и будем

называть показателями; введем для них следующие обозначения:

X =!-—• X = — — р ~ X др 5 т~ X дТ

Тогда уравнение (6.6′) перепишется так:

dX dp. ^ dT

X р р т т

казатель равен показателю степени в формуле указанного вида.

Применение в формулах приведения показателей Хр и Хт

дХ дХ *

вместо частных производных — и — удобнее потому, что,

во-первых, показатели эти безразмерны, а во-вторых, во многих случаях применяемые показатели в довольно большом диапа­зоне изменения параметров, от которых они зависят, могут быть приняты постоянными. В частности, если зависимость характери­стики X от р и Т выражается степенной формулой, то показатели равны соответствующим показателям степени.

В большинстве случаев показатели, применяемые в форму­лах приведения, зависят от сравнительно небольшого числа пара­метров и благодаря этому для определения показателей могут быть использованы несложные графики.

Существенно также отметить, что при пользовании показа­телями достаточно знать только закон изменения характеристи­ки X, но нет необходимости знать все постоянные коэффициенты б зависимостях типа (6.5). При пользовании же частными про­изводными необходимо знать все эти коэффициенты, для того чтобы по уравнению типа (6. 6) найти дифференциал X.

Обычно отклонения температуры и других величин от стан­дартных сравнительно невелики. Относительная величина от­клонения температуры от стандартной для одной и той же баро-

8*

метрической высоты в редких случаях превышает 710/о. Величина отклонения давления воздуха в фактических условиях рф от дав­ления на стандартной высоте /?ст зависит от того, какая высота принята в методе приведения в качестве стандартной. Обычно

эту высоту выбирают так, чтобы отношение — было доста-

Р

точно малым и не превышало в крайних случаях 10—20%. В свя­зи с этим при приведении принято рассматривать конечные при­ращения величин при переходе от фактических условий к стан­дартным как дифференциалы, т. е. считать

= Ър = рст-рф = аР, ЪТ= Тст — Тф — dT

И т. д.

На основании этого при выводе формул приведения обычно применяется следующий метод вывода поправок для перехода к стандартным условиям. Составляют основное уравнение ти­па (6.5), определяющее интересующую нас величину. Затем это уравнение дифференцируют и получают уравнения ти­па (6.6) или (6.8), из которых определяют дифференциал иско­мой величины, рассматриваемый как поправка при пересчете данной величины к стандартным условиям, т. е.

Хст = Хф + ЬХ=Хф + йХ.

В некоторых случаях ошибка, связанная с тем, что мы конеч­ные приращения величин приравниваем их дифференциалам, может быть слишком велика; обычно это бывает в тех случаях, когда показатели Хр или Хт резко изменяются, в зависимости от величины тех или иных параметров. В таких случаях для уточ­нения величины поправки SX при переходе от фактических к стандартным условиям можно использовать один из следующих способов.

Пусть Хр и Хт являются функциями от р, Т и X: Хр=Хр(р, Т,Х),

Хт—Хт(р, Т, Х).

По уравнению (6. 8)

ьх=х(хр^+хтЦ^.

При приведении МЫ переходим ОТ Рф К рст, ОТ Тф к Тст и от Хф к Х„. Если бы Ьр и ЬТ были бесконечно малыми первого порядка, то с точностью до бесконечно малых второго порядка МЫ МОГЛИ бы ВЫЧИСЛЯТЬ Хр и Хт В точке (рф, Тф, Хф) или в точке (рст, Гст, .ЛГСТ). Однако, так как Ьр, ЬТ и ЬХ конечные величины, то точнее определять Хр И Хт для точки

(Рср> ^ср> *ср)>

где

Поскольку оХ вначале неизвестно, воспользуемся способом последовательных приближений. В качестве пер­вого приближения определяем Хр1 и ХТ1 В точке (рфу Гф, Хф) и находим ЪХ по формуле

определяем Хр2 и ХТ2 во втором приближении, а затем вычисляем

Процесс этот продолжаем до тех пор, пока значения $Хг и SXi+1 двух последовательных приближений будут мало отличать­ся друг от друга (например, меньше, чем на 0,2% от X). После этого находим окончательно Л^=Лф+<&Л’г.

Другой способ последовательных приближений заключается в том, что приращения 8р и ST разбивают на ряд небольших интервалов 8рь 8р2, 8р3… и 8ГЬ 8Г2, 8Г3… и находят после­довательно SXi и Хг для каждого интервала.