АНАЛИТИЧЕСКИЕ МОДЕЛИ ПОКАЗАТЕЛЕЙ ЭФФЕКТИВНОСТИ

Комплексный показатель целевой надежности системы (2.13) может быть представлен в следующем виде:

і

/? = 1 — |>в (У) dFn (у), (2.87)

о

где у — нормированная реализация конечного результата функционирования системы (0<у<1).

С помощью предложенных в параграфе 2.2. функций FB(y) и FH{y) на основе модели (2.87) может быть получено 16 частных моделей. Однако, теоретический интерес и практическую значи­мость представляют лишь четыре модели: ступенчатая, линейная, экспоненциальная и нормальная.

Ступенчатая модель эффективности. Ступенчатой будем называть модель, основанную на ступенчатой функции рас­пределения необходимого конечного результата (2.83) и произволь­ной функции распределения возможного конечного результата функционирования системы. Общая ступенчатая модель эффектив­ности получается путем подстановки значения Fn(y) из выражения (2.83) в :(2.87):

R=l-F,(y). (2.88)

В качестве FB(y) может быть использована любая известная функция распределения. Ниже приводятся частные ступенчатые модели эффективности для четырех наиболее типичных видов функ­ции FB(y): ступенчатая

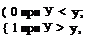(2.89)

ступенчато-линейная

R — 1 — У, о < у < 1;

ступенчато-экспоненциальная

R = е~*вУ; (2.91)

ступенчато-нормальная

Я = (2.92)

Пример 1. Возможный конечный результат функционирования системы ха­рактеризуется величинами рв = 0,8 и 0В=О, О5. Определить вероятность выпол­нения системой поставленной задачи, если необходимый .конечный результат ха­рактеризуется ступенчатым законом. распределения с параметром у = 0,7. За­кон распределения возможного конечного результата функционирования системы не известен.

Решение.. 1. Предполагаем, что закон распределения возможного конеч­ного результата функционирования системы ступенчатый с параметром У=0,8. По формуле (2.89) определяем #i=l, поскольку У>у. Заметим, . что здесь мы приняли Ов = 0. Если учтем, что сгв=0,05 и примем У = цв—Зсгв = 0,8—3-0,05 = = 0,65, то получим R, = 0.

2. Предполагаем, что закон распределения возможного конечного результа­та функционирования системы линейный. То-гда по формуле (2.90) при у—0,7 получаем #2=0,3.

3. Предполагаем, что закон распределения возможного результата функцио­нирования системы экспоненциальный с параметром

ав= 1/>в= 1/0,8= 1,25.

‘Подставляем ав=1,25 и ук = 0,7 в формулу (2.91) и с помощью табл. 4 приложения определяем #з = 0,4.

4. Предполагаем, что закон распределения возможного конечного результа­та функционирования системы нормальный с параметрами Цв — 0,8 и ав=6,05. Тогда при у=0,7-по формуле (2.92) с помощью табл. 2 приложения получаем

Д* = Ч^5?Н'<2>-0’98’

Полученные четыре различные оценки для интересующей нас вероятности #1 = 1, #2 = 0,3, #з=0,4 и #4=0,98 свидетельствуют о том, что при ступенчатом законе распределения необходимого конечного результата функционирования

системы значение комплексного показателя целевой эффективности системы R существенно зависит от вида функции FB(y), поэтому выбор вида этой функ­ции должен быть достаточно обоснованным. На основании качественного ана­лиза использованных видов FB(y) можно сделать вывод, что в данном случае наиболее обоснованной является нормальная функция FB(y)н, так как при сту­пенчатой и линейной функциях необходимо, чтобы ав = 0, а при экспоненциаль­ной Цв=>СГв, чего в рассмотренном примере мы не имеем.

Линейная модель эффективности основана на ли­нейной функции распределения необходимого конечного результата функционирования системы и произвольной функции распределе­ния возможного конечного результата функционирования системы. Для получения линейной модели эффективности подставляем в (2.87) значение F^(y), определяемое по формуле (2.84), и при и г/н=1 получаем

і і

R=l-[FAy)dy—- Ґ ydFB (у) = |i„- (2.93)

‘о о

Следовательно, при линейной функции распределения нормиро­ванного необходимого конечного результата функционирования си­стемы (0^г/^1) комплексный показатель целевой надежности R численно равен математическому ожиданию возможного нормиро­ванного результата функционирования системы цв при любом за­коне распределения последнего.

Поскольку математическое ожидание рв является комплексным показателем целевой производительности системы, приходим к вы­воду, что при линейном законе распределения нормированного ре­зультата функционирования системы имеет место равенство

Mq = R,. (2.94)

т. е. нормированный’ комплексный показатель (критерий) целевой производительности системы Л40 численно равен комплексному по­казателю целевой надежности системы R. Следовательно, комп­лексный показатель R является не только показателем целевой на­дежности, но и показателем (критерием) целевой производитель­ности системы.

Переход от нормированного комплексного показателя целевой производительности системы М0 к ненормированному комплексно­му показателю М в соответствии с (2.27) осуществляется с по­мощью равенства Л4 = ЖГ]М0 или с учетом (2.94):

М = MaR. (2.95)

Экспоненциальная модель эффективности. Экс­поненциальной моделью эффективности системы условимся назы­вать модель, основанную на экспоненциальных функциях распре­деления необходимого и возможного конечных результатов функ­ционирования системы. Для построения этой модели необходимо подставить (2.81) и (2.85) в (2.87) и произвести соответствующие преобразования. В результате получим

R « 1 — е^Ч (2.96)

В данном выражении величина R зависит от отношения рв к іін, Поэтому последние могут быть и ненормированными.

Пример 2. План предприятия задан математическим ожиданием рп=200 ед., а производственные возможности предприятия по выполнению плана оценива­ются математическим ожиданием Цв = 210 ед. Определить вероятность выполне­ния предприятием плана.

Решение. По формуле (2.96) с помощью табл. 4 приложения опреде­ляем

R = 1 — e-‘2I°/200 = 1 — е"1-05^- 1 —0,35 = 0,65.

Это означает, что среди элементарных факторов, определяющих конечный результат производства данного предприятия, 65% таких, которые благоприятст­вуют вьюолнению плана. Несмотря на то, что ц„>рн, целевая надежность про­изводства данного предприятия невысокая. Объясняется это тем, что в данном „ случае имеет место разброс Ун и FB, который характеризуется среднеквадратич­ными отклонениями сгн = У20О и ств=У210.

Нормальная модель эффективности. Условимся на­зывать нормальной моделью эффективности системы такую модель, которая основана на нормальных функциях распределения воз­можного и необходимого конечных результатов се функционирова­ния. В результате подстановки (2.82) и (2.86) в (2.87) получаем

я = л(о*в-і*а)/ V4 ■ %;). ‘ (2.97)

При проведении расчетов по этой формуле не требуется норми­рования конечного результата функционирования системы, посколь­ку аргумент функции FT(z) является безразмерным.

Пример 3. По условиям, данным в примере 2, определить R, если а„=20 ед. И Оц= 10 ед.

Решение. По формуле (2.97) с помощью табл. 2 приложения получаем

( 210 — 200 ‘
(/202+ 102 ;	1 Л 22 )

R =

FT

= FT (0,46) = 0,68.

Комплексный показатель целевой производительности системы

в соответствии с выражением (2.3)

Так как показатель М представляет собой математическое ожи­дание конечного результата функционирования системы, то для его расчета, очевидно, справедливы приведенные выше формулы ма­тематического ожидания случайной величины. Так, при биноми­нальном распределении конечного результата функционирования системы в соответствии с выражением (2.46) имеем

М = пр, (2.99)

еде р — вероятность получения требуемого конечного результата функциониро­вания системы при единичной операции; п — число операций.

Если распределение конечного результата функционирования системы подчинено закону Пуассона, то

М = .

Аналогично рассматривая другие возможные законы распреде­ления конечного результата функционирования системы, можно записать формулы, выражающие зависимость показателя М от па­раметров функции распределения. Следовательно, вопрос опреде­ления показателя М решается достаточно просто, если известен закон распределения возможного конечного результата функцио­нирования системы. Если же этот закон неизвестен, то определе­ние показателя М может быть произведено через показатель Д с помощью аналитических функций, связывающих эти показатели.

Зависимость М от Д для линейной модели эффективности (2.95) установлена. При экспоненциальной модели эффективности (2.96) между М и Д существует взаимосвязь

м

/?= 1-е. (2.101)

При нормальной модели эффективности (2.97) имеем

R = FT (м -(*„)IV’[8]m + <£). (2-І02)

С помощью формул (2.101) и (2.102) можно произвести расче­ты, составить таблицы и построить графики, позволяющие по ве­личине Д определять величину М и наоборот.

Таким образом, если имеются аналитические выражения для функции Ftf(y) или построены математические модели для комп­лексного показателя целевой надежности системы Д, то комплекс­ный показатель целевой производительности определяется доволь­но просто. Болес того, показатель М может быть вычислен и в тех случаях, когда аналитическое выражение функции FB(y) неиз­вестно. Тогда используют известные из теории вероятностей пра­вила вычисления математических ожиданий функций по известным математическим ожиданиям аргументов. Для этого суммарный конечный результат функционирования системы У представляют в виде линейной функции

. — Y=±Yj,

7= 1

где Yj — слагаемые конечного результата функционирования системы, для ко­торых известны математические ожидания М3- и средние квадратичные отклоне­ния О].

4 В соответствии с теоремой сложения математических ожиданий

М = y, Mj. (2.104)

7 = 1

:Если Yj независимы, то среднее квадратичное отклонение

Если же Yj(j= 1, п) зависимы, то а определяется с учетом кор­реляционных связей между величинами Y3-(/= 1, п). В этом случае для определения сг может быть использована следующая прибли­женная формула:

в = а’ — г (а’ — о"), (2.106)

где а’ — среднее квадратичное отклонение Y, определяемое по формуле (2.105); а" — максимальное значение среднеквадратичного из а, т. е. ст"=тах{03|/=

= 1, и}.’ г—’Коэффициент зависимости величин У3-(/= 1, я), который заключен в границах 0^г<1.

В том случае, когда информация о величине г отсутствует, принимают г=0,5, т. е. вычисляют <ху но формуле

а = Т(з’+0")’ (2.107)

Пример.4. Конечные результаты трех предприятий характеризуются оцен­ками: Мi = 20;‘ М2 — 30 и — Л43=40 ед. Среднеквадратичные отклонения оценок:

°М1 = 2: °Л12 = 31 аж3 = 4 ед.

Определить оценку и среднее квадратичное отклонение суммарного конеч­ного результата работы предприятий в предположении, что конечные результа­ты работы независимы.

Решение. По формуле (2.104) вычисляем

М = 20 + 30 + 40 = 90 ед., а по формуле (2.105) определяем, что

а — -)У22 -(- З2 + 4^ = ~j/29 ~ 5,4 ед.

Пример 5. По условиям, заданным в примере 2.4, определить М и а в пред­положении, что коэффициент зависимости конечных результатов работы. отдель­ных предприятий z—ОД

Решение. Поскольку, на величину М не влияет степень зависимости слага1 емых результатов, она остается той же, что и в примере 4, т. е. Л4 = 90 ед.

■Среднее квадратичное отклонение в данном случае определяется по форму­ле (2.106):

а = 5,4 — 0,8 (5,4 — 4) = 4,3 ед.

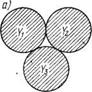
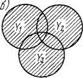
Математическая модель (2.104) называется моделью непересе — кающихся эффектов (рис. 2.3). Если в действительности конечные результаты функционирования подсистем данной системы пересе­каются, то модель (2.104) дает завышенный результат. Такое по­ложение имеет место, например, при расчете валового продукта. Учесть пересечение эффектов при расчете показателя можно с по­мощью следующей модели:

44о = 2 АГ0 j — 2 ^0 U + 2 Мо U* +•••+(- 1 )"-1 440 *, (2.108)

7=1 J<i i<j<&

где Ма— математическое ожидание нормированного конечного результата функ­ционирования системы; M0j — математическое ожидание нормированного конеч­ного результата функционирования j-й подсистемы (/=1, л); М0ц—математиче­ское ожидание нормированного совместного конечного результата функциони­рования трех подсистем (і</</г|/=1, я); М0ц, к — математическое ожи­дание нормированного совместного результата функционирования всех п под­систем.

Нормирующий коэффициент Лїн должен быть для всех конеч­ных результатов (суммарного и частных) один и тот же. Средне­квадратичное отклонение в дан­ном случае определяется по фор­муле (2.106).

Пример 6. По условиям, заданным в примере 2.4, определить М и о с уче­том пересечения эффектов. Нормирую­щий коэффициент Л1н =100 ед.

Решение. Определяем НОріМИрО — вавные конечные результаты функционирования подсистем: М0і = 0,2; Мог = 0,3; М03=0,4.

По формуле (2.108) вычисляем величину М0:

М0 = (0,,2 + 0,3 + 0,4) —(С,2-0,Э+0,2-0,4 + 0,3-0,4) +0,2 ■ 0,3 • 0,4 = 0,66.

По формуле (2.94) определяем М=М0МН =0,66 ■ 100=66 ед.

Среднее квадратичное отклонение будет то же, что и в примере 5 (сг= =4,3 ед.). Сопоставив полученный результат (М=,66 ед.) с тем, который был получен в примере 4 без учета пересечения эффектов (М = 90 ед.), приходим к выводу, что неучет пересечения эффектов в данном примере приводит к завы­шению конечного эффекта примерно на 36%.

Комплексный показатель целевой экономичности системы пред­ставляется как

оо

S=^udF(u). (2.109

Основная трудность практической реализации этой модели со­стоит в выборе функции F(u). Поскольку ресурсы U могут быть разнородными, то

U=%UJt (2.110)

/= і

где Uj — необходимый расход j-го ресурса (/=1, п).

При этом

S= %Sj (2.111)

i=і

или

So = 2 S0j— 2 So<y +- 2 Soijk ••■ + ( 1)” Sq /у,(2.112)

ji = l i<j i<j<k

Связь между S и S0 определяется формулой

• s = s0s„, (2.113)

где S0 — нормированный комплексный показатель целевой экономичности сис­темы; 5Н —нормирующий множитель (коэффициент), который должен быть одинаковым как для суммарного, так и для слагаемых ресурсов.

При использовании формул (2.111) и (2.112) величины S-; оп­ределяются с помощью математических моделей, построенных на основе исходной (2,109). Это означает, что во всех случаях необ- т

ходимо иметь аналитические выражения для F(u) или F(Uj), j = = 1 ,n.

По^ аналогии с выражениями (2.79) — (2.82) для функции рас­пределения необходимых ресурсов можно предложить следующие математические модели:

ступенчатая ( 0, если и < И„; F(u) с = .. ■ ( 1, если U > ин; (2.114) линейная { и/«н при 0 < U < и„; 7г(м)л = { . гг ( 1 при U > и„; (2.115) экспоненциальная F (м)э = 1 — Те “£«, 0 < и < оо; (2.116) нормальная F (й)„ = FT (и — >.u)hu при > За„, (2.117)

где р„ и Ои — математическое ожидание и среднее квадратичное отклонение не­обходимого’ ресурса.

Если параметры приведенных выше функций распределения не­обходимого ресурса известны, то определение комплексного пока­зателя целевой экономичности системы не вызывает затруднений. Так, если функция распределения необходимого ресурса ступенча­тая, то 5 = ын, если F(u) линейна, то S = 0,5uH.

Для экспоненциальной и нормальной функций распределения необходимого ресурса комплексный показатель экономичности си­стемы определяется как 5 = ‘

Важное значение для построения математических моделей комплексного показателя экономичности системы 5 имеют связи между показателями М, R и 5 в форме (2.22) и (2.24), а также математические модели комплексных критериев эффективности системы (2.27). В том случае, когда целью функционирования си­стемы является получение заданного конечного результата при ограниченном расходе ресурса, по формуле (2.22) определяем

S^SJR.

С учетом (2.113) из этого выражения следует

Sq = R. (2.118)

Если целью функционирования системы при многократном ее применении является получение максимального суммарного конеч­ного результата при ограниченном расходе ресурса, то в соответ­ствии с (2.24)

S==SH/Af0. . (2.119)

После подстановки полученного выражения в (2.27) получаем

S0 = M0, ‘ (2.120)

т. е. в случае, когда целью функционирования системы является получение максимального суммарного результата при ограгшчен-

ком ресурсе, комплексный критерий целевой экономичности систе­мы Sо численно равен комплексному критерию производительности системы М0.

Наконец, если целью системы является обязательное получение заданного конечного результата при неограниченном расходе ре­сурсов, математическое ожидание расхода ресурса на получение заданного конечного результата

S = Sx//? ‘(2.121)

где S4—расход ресурса в данном цикле функционирования системы; R(Si) — вероятность получения заданного конечного результата при одном цикле функ­ционирования системы и расходе ресурса S4.

Циклы повторяются до тех пор, пока цель функционирования системы не будет достигнута. Полагая, что 5 является минималь­но необходимым расходом ресурса для достижения заданной цели, комплексный критерий экономичности системы в соответствии с (2.27) определится как

Sq = Si/S или S0 = Я (SO. (2.122)

Следовательно, в том случае, когда целью функционирования системы является получение заданного конечного результата при неограниченном расходе ресурса, комплексный критерий целевой экономичности численно равен вероятности достижения цели при одном цикле функционирования системы R(S{) с расходом ресурса в каждом цикле Si. Функционирование системы после каждого цикла контролируется и прекращается только по достижении за­данного конечного результата. Сказанное справедливо и в том слу­чае, когда к выполнению задачи привлекается несколько систем.

Пусть перед специальным авиаподразделением поставлена задача разведки некоторого объекта в труднодоступном районе. Вероятность обнаружения объ­екта щря одном вылете самолета равна R(Si), где Si — затраты ресурсов на один вылет. Вылеты повторяются одним и тем же самолетом или несколькими самолетами данного типа до тех пор, пока объект не будет обнаружен. Матема­тическое ожидание затрат ресурсов S в данном случае будет определяться по формуле (2.121), а целевая экономичность операции оцениваться критерием S0 (2.122). По смыслу задачи в качестве комплексного показателя целевой эконо­мичности системы может быть использовано также математическое ожидание числа вылетов для выполнения заданной цели:

N = S/Sl.

‘Как итог анализа моделей комплексных показателей и критериев эффектив­ности систем воздушного транспорта отметим удобство этих моделей при прак­тическом использовании, наглядность и низкую трудоемкость расчетов. При анализе этих моделей установлено:

1. В случае линейных моделей эффективности комплексный критерий целе­вой эффективности является в то же время комплексным критерием целевой производительности и целевой экономичности системы. Для моделей, отличных от линейных (например, экспоненциальной и нормальной), между показателями и критериями также существует взаимосвязь, позволяющая по известным комп­лексным показателям эффективности вычислять комплексные критерии эффек­тивности, и наоборот.

2. Существуют три типичных случая, для которых выявлена комплексная оценка эффективности системы. Для промежуточных случаев комплексные оцен­ки хотя и менее определенны, однако возможны.

3. Исходным пунктом разработки математических моделей показателей и критериев эффективности является наличие аналитических выражений для функ­ций распределения конечного результата функционирования системы и функции распределения необходимого расхода ресурсов на получение заданного конеч­ного результата функционирования системы.

Рассмотренные аналитические модели позволяют строить комй — лексные показатели и критерии эффективности систем воздушного транспорта по известным параметрам и единичным показателям функционирования систем. Однако в практике исследования эф­фективности воздушного транспорта могут встретиться такие слу­чаи, когда для использования аналитических моделей нет необхо­димых исходных данных. Тогда ищут другие пути решения постав­ленной задачи, к которым относятся натурные и машинные экспе­рименты, а также решение задач оценки эффективности с помощью статистических моделей.