СТАТИСТИЧЕСКИЕ МОДЕЛИ ПОКАЗАТЕЛЕЙ ЭФФЕКТИВНОСТИ

Под статистическими моделями эффективности сложных систем понимаются математические отношения, позволяющие ‘определять покааатели и критерии эффективности по статистическим данным. В практике исследования эффективности сложных систем и про­цессов используются следующие статистические модели: точечных и интервальных оценок показателей и критериев эффективности; статистической проверки гипотез о показателях и критериях эф­фективности; статистической проверки гипотез о функциях распре­деления „конечных результатов функционирования систем и функ­циях распределения необходимого расхода ресурсов для получения заданного конечного результата функционирования системы; кор­реляционного и регрессионного анализа показателей и критериев эффективности; объединения информации о показателях и крите­риях эффективности и др.

Статистические модели оценки показателей и критериев эффек­тивности — это математические выражения, представляющие собой выборочные функции, используемые в качестве статистических оценок соответствующих показателей и критериев эффективности. Обозначим через 0 интересующий нас показатель эффективности и рассмотрим порядок построения математических моделей для точечной и интервальной оценок показателя 0 по статистическим данным.

Предположим, что для определения показателя 9 проведено п независимых и свободных от постоянной погрешности испытаний и получены результаты

в;, ей,…. е}…… 0„.

точность которых характеризуется средними квадратичными откло­нениями

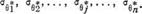(2.124)

Задача состоит в том, чтобы по имеющейся информации опре­делить точечную и интервальную оценки для показателя 0.

Точечной оценкой показателя 0 называется выборочная функция

0*=/(б}. Че*), ]=,п,

которая может быть принята в качестве приближенного значения показателя 0. Приняв 0 — 0*, мы допустим случайную ошибку.

89* = 0* — G,

которая характеризуется средней квадратичной а 0в*. Решение по­ставленной задачи сводится к определению такой выборочной функции, которая будет удобна для практического использования, является несмещенной оценкой показателя 0 и обладает наиболь­шей точностью (минимумом дисперсии).

Чтобы удовлетворить первому требованию, необходимо взять выборочную функцию (2.125) линейной, т. е.

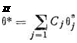(2.127)

Е [8*] = 9,

2 СjE [0*] = 0.

Второе условие будет выполнено, если будет иметь место ра­венство

Поскольку по условию’ задачи £[О.;*] = 0, то равенство (2.129)

будет выполняться при 2 <4 = 1 •

1-І

/5[0*]= VC72D[0*]+min.

Третье условие будет справедливо при

-Таким образом, математическая модель для определения коэф­фициентов Cj будет иметь вид:

где D[0j*]— дисперсия случайной величины 9,*.

Эта модель отражает нелинейную задачу математического про­граммирования. Решив ее методом неопределенных множителей Лагранжа, получим

(2.132)

— UD [0*]=1/а2

J О •

После подстановки значения Cj из (2.132) в (2.127) и (2.130) получаем следующие рабочие формулы:

і е* = (2.!33)

7-і • / 7=1

V=1/j/i^. (2Л34)

В свою очередь вес 6* оценки

4i =!/<&■ (2.135)

е7

Определяемая по формуле (2.133) оценка >0* является несме­щенной и обладает минимальной дисперсией п62„, рассчитанной по формуле (2.134).

Пример 7. Часовая производительность самолета Ан-24 определялась в трех подразделениях и получены следующие оценки (т.-км/ч):

А* = 1600; Л2 =1700′> А* = 1650.

Средние квадратичные отклонения оценок аА* = 100; Од* = 150; a^| = 80.

Определить объединенную оценку часовой производительности самолета,4* и ее среднее квадратичное отклонение

Решение. Определяем по формуле (2.136) вес оценок A

qx = 1/1002 ^0,0001; q2 = 1/1502 = 0,0000445; q3 = 1/802 = 0,000156;

Вычисляем сумму весовых коэффициентов

41 + 42 + 4з = 0,0001 + 0,0000445 + 0,000156 = 0,0003005,

Для удобства расчетов принимаем qi=. Тогда

з

<72 = 0,445;- <73= 1,56 .и ^q’t = 3,005^3.

■ 7-і

Вычисляем по формуле (2.133) объединенную оценку А*:

А* = (q[ А* + 4г + 4з Аз)/(4І + q’2 + 4з) =

= — і — (1-1600 + 0,445-1700 + 1,56-1650) = 1643,5 т-км/ч. ‘

О

Вычисляем по формуле (2.134) среднее квадратичное отклонение ад* = 1/уС0,003 к 58 т-км/ч.

На основании формул (2.133) и (2.134) могут быть получены формулы для ряда частных случаев.

Случай 1. Оценки (2.123) равноточны, т. е. <*,<=«• В этом случае

7-і

0()* = п-

Пример 8. По условиям, данным в примере 7, определить объединенную оценку часовой производительности самолета А* и ее среднее квадратичное отклонение ад„. , если точность каждой частной оценки Aj* характеризуется средним квадратичным отклонением 0=150 тк • м/ч.

По формуле (2.128)

А* = — (1600 + 1700 + 1650)= 1650 т-км/ч.

О

150

Определяем по выражению (2.137) <гА* =—— ~ 87 т-км/ч.

у 3

Случай 2. Имеются только две частные оценки показателя 0, т. е. п = 2. В этом случае формулы (2.1-33) и (2.134) имеют следующий вид:

+.у о-»»

« “«= ли.: / |А/+ + ■ (2.139)

Пример 9. Проектная оценка комплексного показателя целевой производи­тельности данной системы и ее среднее квадратичное отклонение:

М* = 220 ед, ам* = 10 ед. ‘

По. результатам опытной эксплуатации системы определены оценка данного показателя и ее среднее квадратичное отклонение М2 = 200 ед-и ам* =5 ед.

Требуется объединить полученные оценки.

По формулам (2.1.38) и-(2.130) вычисляем:

М* — (52-220 + 102-200)/(Ю2 + 52)« 204 ед.;
аж*= 10-5//Ї02 + 52«зЗ,2 ед.

С помощью точечных оценок могут быть получены приближен­ные значения интересующих нас показателей и средние квадра­тичные отклонения і (ошибки) приближенных значений. Их недо­статком является то, что она не содержат информации о границах интервала, в пределах которого находится истинное значение дан­ного показателя, т. е. с помощью точечной оценки и ее среднего квадратичного отклонения мы не можем определить величину ошиб­ки приближенного равенства 0»0*. Ответ на этот вопрос может быть получен с помощью интервальных (доверительных) оценок.

Интервальная оценка показателя 0 определяется на ос­новании следующего уравнения:

Y = Вер {(6* — 0| < є}, (2.140)

где 0 — истинное значение показателя эффективности; 0* — точечная оценка того же показателя; у— достоверность интервальной оценки (вероятность того, что истинное значение показателя эффективности заключается в интервале 0*—ег^О<0* + е); е — точность интервальной оценки показателя эффективно­сти (половина доверительного интервала, содержащего с вероятностью у истин­ное значение показателя эффективности).

На основании уравнения (2.140) могут быть построены следую­щие рабочие формулы для определения интервальных оценок:

в = в*±*7в#, (2.141)

і

или

0 = 0* ± *Т ®в** (2.142)

где и — коэффициенты достоверности интервальной оценки, определяемые с помощью табл. 5 и 6 приложения соответственно.

Формула (2.141) используется в том случае, когда исходная информация о показателе эффективности 0 задается статистичес­ким рядом оценок 0j* (2.123) и соответствующим рядом средних квадратичных отклонений °е* (2.124) оценок вД т. е., когда а0*.

известны. В этом случае выборочная функция * = (0* — ®)/v име’ ет нормальное распределение и поэтому коэффициент Zy определя­ется с помощью таблицы квантилей нормального распределения (табл. 5 приложения). Входом в табл. 5 является порядок кванти­ля (рис. 2.4)

Р =(1 + Y)/2. (2.143)

Пример 10. По условиям, данным в примере 9, определить доверительный интервал для показателя производительности системы М с достоверностью у=0,9. 1

Поскольку средние квадратичные отклонения объединяемых в — примере 9

оценок М * и М2 известны, доверительный интервал показателя М определя­ется по формуле (2.141). Для этого ло (2.143) вычисляем р— (1 +0,9)/2 = 0,95 и по табл. 5 приложения определяем z0,9 = 1,64. После этого — подставляем в фор­мулу (2.141) значения М* = 204 ед., ам* = 3,2 ед, — 1,64 и получаем М = 204± 1,64 • 3,2 = 204-±5,2 или 198,8 <М< 209,2.

Следовательно, с — вероятностью 0,9 можно утверждать, что истинное значение показателя" М в условиях данного примера находится в интервале, границами которого являются числа.: 198,8 ед. и 209,2 ед., т. е. что Af= 198,84-209,2.

Формула (2.142) используется в том случае, когда исходная информация о показателе эффективности 0 задается только рядом статистических оценок 0-j* (2.123), средние квадратичные откло­нения которых °е*. не известны. В этом случае предполагают, что все 0j* (2.123) равноточны, независимы и свободны от постоянной погрешности и определяют оценку среднего квадратичного откло­нения генеральной совокупности, из которой сделана выборка

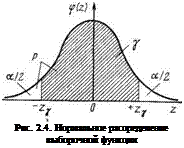/———— я

■°* = |/ ^^(а;-6*)2, (2.144)

0*. (2.145)

При этом среднее квадратичное отклонение оценки

oe* — a*/Vn. (2.146)

f = (0*_e)/oj, (2.147)

имеет распределение Стьюдента, и поэтому коэффициент k оп­ределяется с помощью таблицы квантилей распределения Стью­дента (табл. 6 приложения). Входами в эту таблицу являются по­рядок квантиля р (2.143) и число степеней свободы k=n—1.

Пример 11. По условиям, данным в примере 9, определить доверительный интервал для показателя производительности системы с достоверностью y^O.9 в предположении, что средние квадратичные отклонения оценок АЦ* и Мг* не известны.

По формулам (2.145), (2.144) и (2.146) вычисляем:

0* = — у (220 + 200) = 210 ед.;

с* = |/ ~j [(220 — 200)2 + (200 — 210)2] as 22 ед.;

— 21 , 2?д 14 ел.] |

При значениях р==0,95 и k= по табл. 6 приложения определяем U 9: <= = 6,31. По формуле (2.142) вычисляем 0 = 210±6,3-1 -14 = 210 + 88 или 122s£0< <298.

Следовательно, по условиям данного примера с вероятностью 0,9 можно ут­верждать, что истинное значение показателя целевой производительности систе­мы находится в пределах 122-4298. Сопоставив результаты примеров 10 и И, можно установить роль средних квадратичных отклонений <г0* исходных оце­нок 0j* при определении точечных и интервальных оценок показателей эффек­тивности.

В том случае, когда точечная оценка среднего квадратичного отклонения показателя эффективности а* определяется по форму­ле (2.144), интервальная оценка может быть найдена с помощью неравенств

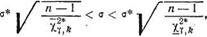(2.148)

—2* 2* о — _

где и ~квантили Х2“РаспРеДеления» определяемые по табл. 7 прило — жения. При определении х^*й входами в нее являются р — (1 4- у)/2 и к = п — 1 а при определении соответственно /> = (1 — у)/2 и к = п— 1. Выборочная функция ^-распределения имеет вид:

Х2=(я — 1)а*7а2, ■ (2.149)

где сг*2 — оценка дисперсии сг, определяемая по формуле (2.148).

Пример 12. По условиям, данным в примере 11, определить интервальную оценку для (Т с доверительной вероятностью у —0,9.

На основании табл. 7 приложения по р’ = (1 — Y)/2 = (1 —0,9)/2= 0,05 и А = и— 1 = 2— 1 = 1 определяем хо, э; і = 0,004, а по д" = (1-НУ)/2 = О + -4- 0,9)/2 = 0,95 и k = 1 определяем x<j, э; і = 3,84. По формуле (2.148) вычис­ляем:

a-,/ A" L = 14 I / — і— = 7:

. V Х& V 3,84

я* f — W.3.L = и /1/0,0°4: 7°; 7 < а < 70 ед. г *Т;й

Следовательно, с. вероятностью 0,9 можно утверждать, что среднее квадра­тичное отклонение распределения частных оценок показателя 0 находится в пре­делах от 7 до 70. Низкая точность объясняется тем, что оценка а* определя­лась только по двум частным оценкам.

Рассмотренные статистические модели определения показате­лей эффективности применимы как для комплексных, так и для единичных показателей. При использовании указанных моделей необходимо проверять гипотезу о принадлежности объединяемых оценок к одной и той же генеральной совокупности.

Проверка гипотезы о принадлежности двух оценок к одной и той же генеральной совокупности производится с использованием критерия

** = IBJ-<&/}/"+ (2.150)

ИЛИ

/* = |0*-e;[/j/a2*+o2* > taJI, (2.151)

где za и —коэффициенты значимости гипотезы Яо : 01 = 02, определяемые по табл. 5-и 6 приложения, соответственно; 0t и 02 — математические ожида­ния оценок 01* и 02* соответственно.

Если выполняется неравенство (2.150) или-(2.151), то гипотеза о принадлежности оценок 97 и 02* к одной и той же генеральной совокупности отвергается. В противном случае указанная гипотеза не отвергается (но и не подтверждается!). Если неравенство (2.150) или (2.151) не выполняется, то вычисляют вероятность

■ «=1-ф(К-в2|/]/Л + Л) (2.152)

и по величине а делают заключение о возможности принятия или непринятия выдвинутой гипотезы, т. е. вероятность а — это уро­вень риска при отклонении гипотезы. Значение функции Ф(г) бе­рут из табл. 3 приложения.

Примерно те же результаты для вероятности а. дает формула

« = 2 [l — Ft (К-‘«Я / У + (2’153)

Формула (2.152) или (2.153) применяется. тогда, когда провер­ка гипотезы о принадлежности 07 и 02* к одной и той же генераль­ной совокупности проводится по критерию (2.150). Если же про­верка указанной гипотезы производится с помощью критерия

(2.151), то в случае неотклонения гипотезы расчет а следует про­изводить по формуле

«=S(K-e;|//<1*+’1;*2), (2.154)

где Sт(г) — табличная функция Стьюдента.

Условия применения критериев (2.150) и [(2.151) те же, что и моделей (2.141) и (2.142). При определении, коэффициентов za и іа входом в табл. 5 и 6 приложения соответственно служит кван­тиль (см. рис. 2.4)

р 1 — а/2. (2.155)

При использовании критерия (2.151) число степеней для входа в табл. 6 приложения определяют по формуле

k — m + n% — 2, (2.156)

где пі и пг — числа результатов испытаний, по которым определялись оценки 01* и 02*.

•Порядок проверки гипотезы #о : 01 = 02 рассмотрим на следую­щих примерах.

Пример 13. Оценки выполнения плана двумя предприятиями Mt*=200 ед и М2* = 210 ед. Средние квадратичные отклонения оценок: Qм ~ ед — и

<j^[*= 15 ед. Можно ли считать, что показатель эффективности работы второго

предприятия выше, чем первого? ‘ •

Проверяем гипотезу о принадлежности оценок Mt* и М2* к одной и той же генеральной совокупности. Если яти оценки принадлежат к одной генеральной совокупности, то разность оценок Mi* и Мг* несущественна и поэтому нет осно­ваний для того, чтобы считать показатель эффективности работы второго пред­приятия выше. Проверку гипотезы H0:Mi = M2 производим в следующем по­рядке:

вычисляем выборочную функцию

г = 1200 — 2101//102 + 152 = 0,56;

задаемся уровнем значимости гипотезы (уровнем риска) а=0,10, вычисля­ем по формуле (2.155) р— 1—0,05=0,95, по р=0,96 входим в табл. 5 приложе­ния и определяем z0,i = 1,64;

в соответствии с критерием (2.100) устанавливаем, что г = 0,5’6 С г0.і = = 1,64. Следовательно, гипотеза Нп:Мі—М2 не отвергается, поэтому нет осно­ваний для того, чтобы считать показатель эффективности работы второго пред­приятия выше первого;

вычисляем по (2.152) е помощью табл. 3 приложения уровень риска а, при котором гипотеза Но : Mi=M2 отвергается: а = 1 — Ф (0,56) = I —• 0,42 = 0,58.

Следовательно, гипотеза о принадлежности оценок Мі* = 2С0 ед. и М2* = = 210 ед. к одной и той же генеральной совокупности может быть отвергнута только с уровнем риска а=0,58;

определяем по формуле

вероятность того, что показатель эффективности работы второго предприятия М2 больше показателя эффективности работы первого предприятия: P(.M2>Mi) = fT(0,56) =0,71. Поэтому с вероятностью 0,71 можно утверждать, что в условиях данного примера показатель эффективности работы второго предприятия выше показателя эффективности работы первого;

Р (ЛІ! > Мз) = Л ^ (МЇ — Ж*) j У °2М+ °м*2 j (2- 15S)

вероятности того, что Mt>M2:

F (Mi >М2) —Fт (—0,56) = 1—Fт (0,56) = 1—0,71 =0,29. Следовательно, несмотря на то, что M2*>AV с вероятностью 0,29 можно утверждать, что в условиях данного примера показатель эффективности работы первого предприятия выше эффективности работы второго.

Пример 14. Оценка показателя регулярности полетов для данного пред­приятия была до проведения некоторых мероприятий по ее повышению Кі*—- = 0,60, после проведения которых стала Кг*— 0,70. Средние квадратичные отк­лонения оценок соответственно равны ^*^*=0,05 и q*k*=0,1. Оценки определя­лись по выборкам пі = 10 и п2 = 6.

Можно ли считать проведенные мероприятия эффективными?

Решение. Для получения ответа на поставленный вопрос проверяем ги­потезу Н о : Кі = Кг,

вычисляем выборочную функцию критерия (2.151)

t= /0,60 —0,70|//0,052 +0,12 = 0,1/0,112=0,89;

задаемся а=0,1 и вычисляем по формуле (2.155) р = 0,25;

■по формуле (.2.156) определяем число степеней свободы 6=10+6—2= 14; при р = 0,95 и 6=14 по табл,- 6 приложения определяем to, і-, u=1,76; в соответствии с критерием (2.151) устанавливаем ^ = 0,89 < tgi;14 = 1,76. Следовательно, гипотеза о принадлежности оценок /бі* = 0,6 и Кг* = 0,7 к одной и той же генеральной совокупности не отвергается, поэтому нет основа­ния считать проведенные мероприятия по повышению регулярности полетов эф­фективными. Разность оценок К і* и Кг* является результатом случайного раз­броса.

Определяем по формуле (2.154) уровень риска а, с которым может быть от­вергнута гипотеза По : Кі=Кг : a=S(0,89) =0,62.

Следовательно, гипотеза о принадлежности оценок ТО* = 0,6 и /С2* = 0,7 к одной и той же генеральной совокупности может быть отвергнута лишь при уровне риска a = 62%. Риск достаточно велик, поэтому следует считать, что проведенные мероприятия по повышению регулярности недостаточно эффек­тивны.

В. ряде случаев в качестве показателя эффективности системы может быть использовано среднеквадратичное отклонение конеч­ного результата или расхода ресурса. При этом также может воз­никнуть необходимость проверки гипотезы о принадлежности оце­нок дисперсии к одной и той же генеральной совокупности.

Проверка гипотезы о приналежносте двух оценок дисперсии af и <+* к одной и той же генеральной совокупности, т. е. гипо­тезы Н0 : + = 021 , производится с помощью критерия

F* = cf/af > FM, (2.159)

где <s‘f и з|* — оценки дисперсии a > af); F k k—коэффициент значимос­ти гипотезы, определяемый по табл, 8 приложения, в которой приведены значе­ния квантиля У’ф.*,.*, распределения выборочной функции

F* = 4*l° Г1 (2.160)

Входом в табл. 8 являются порядок квантиля р = 0,95, отвечаю­щий a=0,Q5, и степени свободы kl = n1—1 и k2=n2—.

Пример 15. В процессе контроля стабильности некоторого производственно­го процесса получены две оценки дисперсии 02*= 16,4 ед2 и Oj* = 22,5 ед2. Число наблюдений, по которым определялись указанные оценки, соответственно, равны: «1=14 и «2=10. Требуется проверить гипотезу о принадлежности полу­ченных оценок к одной и той же генеральной совокупности, т. е. гипотезы Но :а,2=ст22.

Вычисляем по формуле (2.160)

F* = 22,5/16,4= 1,37.

По табл. 8 приложения при р = 0,95, = 13, k2—9 определяем F0,os, ie,9=

= 2,71.

В соответствии с критерием (2.159) имеем

F* = 1,37 < Fqoj. 13; д = 2,71.

Следовательно, гипотеза о принадлежности оценок of = 22,5 ед2 и af = 16,4 ед2

к одной и той же генеральной совокупности не отвергается. Это означает, что нет оснований для принятия решения о регулировании производственного про­цесса.

В том случае, когда возникает необходимость проверки при­надлежности к одной и той же генеральной совокупности более двух оценок, необходимо произвести попарную оценку принадлеж­ности к одной и той же генеральной совокупности всех оценок. Данные оценки принадлежат к одной и той же генеральной сово­купности тогда и только тогда, когда все они попарно принадле­жат к одной и той же генеральной совокупности.

Пример 16. Себестоимость перевозок самолетом Ан-24 определялась на трех предприятиях. Были получены оценки:

С ~ 10 коп/т-км; 4 = 20 коп/т-км; 4 = 25 коп/т-км

и средние квадратичные отклонения оценок:

о * = 2 коп/т-км; а * = 1 коп/т-км; а * = 2 коп/т-км.

С1 с2 . Д

Можно ли считать полученные оценки принадлежащими к одной генераль­ной совокупности?

Но. формуле (2.150) вычисляем:

г2 = 110— 20[/ У22 + 12 = Ю//5 = 4,47;

43 = ЦО — 251 l/W+22 = 15//8 = 5,30; z*23 = J20 — 251// И + 22 = 5//S = 2,24.

Задаемся а = 0,1 и при р=0,95 по табл, приложения определяем z0,і — = 1,64.

В соответствии с критерием (2.150) все рассмотренные гипотезы отвергают­ся. Полученные оценки себестоимости не принадлежат к одной генеральной со­вокупности, следовательно, причина большого разброса значений себестоимости не случайная.

Наиболее трудоемкой и сложной операцией является проверка с помощью статистических критериев, гипотез о законе распреде­ления конечного результата функционирования системы F(y) и необходимого расхода ресурсов F(u), а также законов распреде­ления любых других случайных величин, используемых при оцен-

ке эффективности воздушного транспорта. Рассмотрим порядок решения этой’задачи для функции распределения F(x) некоторой случайной величины X, которая может быть конечным результа­том функционирования системы Y, необходимым расходом ресур­сов U или любой другой случайной величиной.

Проверка гипотезы о законе распределения случайной величи­ны X производится численным методом, основанным на примене­нии критерия х2> разработанного К — Пирсоном. Согласно этому ме­тоду наблюдаемое опытное распределение частот сравнивается с гипотетическим теоретическим распределением соответствующей ге­неральной совокупности. Для этого выдвигается гипотеза о неиз­вестной функции распределения F(х) генеральной совокупности, которая сопоставляется с подходящей выборочной функцией, и в зависимости от величины отклонения опытного распределения от теоретического выдвинутая гипотеза отвергается или не отверга­ется. Так как статистическая гипотеза относится к неизвестной функции распределения F(x), а. не к отдельным ее параметрам, то говорят о непараметрическом методе проверки гипотезы или о кри­терии подобия. Критерий х2 и представляет собой один из таких критериев подобия.

Для проверки гипотезы о функции распределения F(x) по кри­терию X2 строят выборочную функцию

т

х2* = 2 (я* —npiFInpi. (2. 161)

1=1

Вероятность попадания результата наблюдения на данный ин­тервал

Pi == F0 (Х;)~ F0 Oi-i), ‘ (2.162)

где Fo(x)—значение гипотетической функции распределения случайной величи­ны X для аргумента х; я — общее число наблюдений; я,-—число наблюдений в интервале Ах = хі—лцЩ; т—число интервалов.

Критерий значимости гипотезы Н0: F (х) =F0(x) строится в ви­де неравенства

Х2*>Х2;,.. (2-163)

где х2д,— коэффициент значимости гипотезы (квантиль ^-распределения порядка р= 1—а при k степенях свободы, определяемый по табл. 7 приложе­ния).

Задача проверки гипотезы о функции распределения решается в следующем порядке:

1. Производят качественный анализ результатов наблюдений Xj(i=,n) и разбивают область распределения последних на ин­тервалы

Ах і = Х[ — хі_. і. (2.164)

Число интервалов т определяется таким образом, чтобы вы­полнялось неравенство

npi >5, ‘ (2. 165)

где npi — оценка теоретического числа’ результатов наблюдений на данном ин­тервале Лащ

2. Подсчитывают число результатов nt, попавших на интервал АХі.

3. Вычисляют частоты попадания интересующих нас результа­тов наблюдений на интервалы Ах{

р* = n-Jn, . (2. 166)

н статистическую функцию распределения

F* (X) = 2 Ре — (2-167)

Х1<Х

Если случайная величина х непрерывна, то определяют также оценку плотности ее распределения:

/*(*/) = р’/Ьхі. ‘ (2. 168)

4. Строят гистограмму плотности распределения f*(x) статисти­ческих данных и по виду гистограммы выдвигают гипотезу F0(x) о виде функции F(x). При выдвижении гипотезы Н0: F(x) =F0(x) используются ранее рассмотренные функции распределения слу­чайных величин.

5. Вычисляют оценки ц* и ст2*:

т

М’* = 2 Р* (хі + 0,5Д^і); (2- 169)

i = l m

a2* = 2 Vi (XI — 0,5Дх,-)2 — p*2. (2. 170)

i=l

6. По величинам ц* и сг2* вычисляют оценки параметров функ­ции F0(x).

7. Рассчитывают по формуле (2.162) теоретические значения pi.

8. По формуле (2.161) находят значение выборочной функции

X2*-

9. Определяют по табл. 7 приложения коэффициент х2,* • Вхо­дами в табл. 7 являются квантили

р = 1 — а н k = п — 1 — г, (2. 171)

где г — число параметров функции F0(x), определяемых по результатам’ наб­людений.

10. В соответствии с критерием (2.163) принимают решение о выдвинутой гипотезе.

Расчеты ведут с использованием табличных алгоритмов.

Пример 17. В аэропорту с ежедневным числом самолето-вылетов т —10 регистрировались задержки вылетов. Было проведено в общей сложности п — = 200 наблюдений. Число задержек ад вылетов по группам т распределилось следующим образом:

Xi… О 1 2 з 4 56789 10 in… 41 62 45 22 16 8 4 2 0 0 О

Предполагалось, что число задержек Хі имеет распределение Пуассона, так как в нормальных условиях работы аэропорта задержку вылета данного самоле­та можно считать редким событием, которое не зависит от задержки вылета

других самолетов. Требуется проверить, соответствует ли это предположение дей­ствительности.

Решение. Случайная величина X в нашем примере предполагается рас­пределенной по закону Пуассона (2.50)

/ х

р (xt) = (X Чхі) ег Хі = 0, 1, 2,… 10. (2. 172)

Требуется проверить гипотезу

Н0: F (х) = Fq (х) = 2 0х‘/Хі) е_х. (2.173)

Для решения поставленной задачи производим необходимые вычисления.

По формуле (2.166) определяем значения частот р** (табл.

2.1).

Таблица 2.1 Исходные данные Расчетные данные (пГ"Рі)2 (ni~nPi) 2 xi " pi Pi *Р[ пГпРі npt 0 41 0,205 0,1653 33,06 ‘ 7,94 63,0436 1,91 1 62 0,310 0,2975 59,50 2,50 6,2500 0,11 2 45 0,225 0,2678 53,56 — 8,56 72,2736 1,37 3 22 0,110 0,1607 32,14 —10,14 102,8196 3,20 • 4 16 0,080 0,0723 14,46 1,54 2,3716 0,16 5 (8- 0,040 0,0260 5,20 6 4 0,020 0,0078 1,56 7 14 2 0,001 0,0020 7,28 0,40 6,72 45,1584 6,20 8 0 0 0,0005 0,10 9 » 0 0,0001 0,02 10 [о 0 0,0000 0,00 ’ 2 200 1 1 200 0 291,9168 X2*= 12,95

Вычисляем по формуле (2.169) оценку (Л* = 0 • 0,205 — f 1 ■ 0,310 + 2 ■ 0,225 + 3 ■ 0,110 + 4 • 0,080 + 5 • 0,040 + 6 • 0,020 + 7 X X 0,010 =1,8.

Поскольку в рассматриваемом примере имеется в виду провер­ка гипотезы о дискретном распределении, в формуле (2.169) вместо координат центров интервалов x;-|-0,5Ax* использованы значения числа задержек вылетов Х{. Учитывая, что для распределения Пу­ассона имеет место равенство А, = р, оценка параметра распределе­ния (2.172) А,* = р,* = 1,8.

По формуле (2.162) с учетом (2.173) вычисляем теоретические значения вероятностей ри которые соответствуют распределению Пуассона (2.173) при i* = l,8.

По формуле (2.161) вычисляем значение выборочной функции у2* = 12,95. Результаты расчетов сведены в табл. 2.1.

С помощью табл. 7 приложения по величинам р = 0,95 (а=0,05) и k = m—1—г= 6—1—1=4 определяем критерий значимости гипо-

тезы Хо 05-4 — 9,5 и с помощью критерия (2.163) проверяем гипотезу о распределении Пуассона (2.173): х2*= 12,95 > Хо, о5;4-

Следовательно, данная гипотеза в условиях рассмотренного примера отвергается. Необходимо выдвигать и проверять другие возможные гипотезы.

Критерий (2.163) построен в предположении, что случайная ге­неральная совокупность имеет нормальное распределение. Поэтому с помощью этого критерия можно проверять гипотезу лишь о нор­мальном распределении. Однако, как показывает практика, этот критерий дает вполне удовлетворительные результаты при провер­ке гипотез и о других законах распределения, например о биноми­альном, законе Пуассона, Эрланга, Вейнбулла, Рэлея и др.