МАТЕМАТИЧЕСКИЕ МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА И ПРОГНОЗИРОВАНИЯ ПОКАЗАТЕЛЕЙ ЭФФЕКТИВНОСТИ

Под регрессией понимается зависимость математического ожи­дания какой-либо случайной величины от некоторой другой или от нескольких величин. В отличие от функциональной связи у = —f(x), когда каждому значению х соответствует одно определен­ное значение у, при регрессионной связи одному и тому же значе­нию х могут соответствовать в зависимости от случая различные значения у.

Математические модели и методы регрессионного анализа ос­нованы на том, что случайные величины X и У, имеющие совмест­ное распределение вероятностей, связаны вероятностной зависи­мостью: при каждом фиксированном значении Х=х величина У является случайной величиной с определенным (зависящим, от значения х) условным распределением. Регрессия величины У по величине X определяется условным математическим ожиданием У, вычисленным при условии, что Х = х:

. у (а) = Е [У/х]. (2.174)

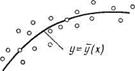
Уравнение у = у(х), в котором х играет роль «независимой» переменной, называется уравнением регрессии, а кривая, соответ­ствующая этой зависимости (рис. 2.5),— линией регрессий. При­чем функции у = у(х) и х=х(у) не являются взаимно обратимыми. Точность, с которой уравнение регрессии У по У отражает измене­ние У в среднем при изменении ‘х, измеряется условной дисперси­ей величины У, вычисленной для каждого значения Х=х:

D [Г/А-] а2 (А). • (2. 175)

Линия регрессии обладает тем свойством, что среди всех дей­ствительных функций f(x) минимум математического ожидания £{(У—f(x)2] достигается для функции f(x)=y(x)=E[Y/x], т,- е. ре­грессия У по х дает наилучшее с точки зрения принципа наимень­ших квадратов представление зависимости У от X. Это свойство линии позволяет использовать модель для прогноза величины У

по известным значениям величины X. Регрессия бывает парной, когда рассматривается система двух вели­чин (У, X), и множественной, когда рассматривается система грех и большего. числа величин

(Р, Xiil=-n)- Парная и множествен­ная регрессии бывают линейными и нелинейными.

Практические методы изучения регрессионной зависимости между величинами по статистическим дан­ным получили название методов регрессионного анализа’. Регрес­сионный анализ включает: определение общего вида уравнения регрессии; построение оценок неизвестных параметров, входящих в. уравнение регрессии; проверку статистических гипотез о регрессии

Пусть требуется произвести прогноз значений некоторого пока­зателя эффективности Y (например, конечного результата функци­онирования системы) для некоторого момента времени 4 при из­вестных значениях этого показателя г/j (/ = 1 ,п) для моментов вре­мени tj{j—,fi).

С помощью регрессионного анализа такое прогнозирование проводится следующим образом.

1. Производят качественный анализ динамического ряда

{(УҐ> tj)j=T7R} (2. 176)

с целью определения наличия корреляционной связи между У И І. При наличии связи строят график распределения статистических данных (2.176) и по виду распределения выдвигают гипотезу о ли­нии регрессии

У (0 = У 4: аД j = 1, п,

где а,- — коэффициенты регрессии.

2. По данным динамического ряда определяют точечные и ин­тервальные оценки коэффициентов регрессии.

3. Проверяют статистические гипотезы о коэффициенте регрес: сии aj и о линии регрессии y(t).

4. С помощью построенной регрессионной модели

У*(4 = У*(4. а*),/= Т77Г ‘ (2.178)

определяют точечную и интервальную оценку математического ожи­дания у (4) рассматриваемого показателя У для заданного момен­та времени 4.

При решении задачи используют известные в теории регресси­онного анализа математические модели. Точечная оценка коэффи­циента корреляции производится по следующим формулам:

или

где

7=1 7=1

t’ = tj—7; у’ ~ yj—(/;

/2 Tl

■ 2 *>;=2

7=1 7=1

І (7;.)2=V

7=1 7=i

I W)s"i ■

7=1 ■ 7=i

Проверка гипотезы о значимости корреляционной связи между У и t производится с помощью критерия

С > t..

Р и, ft*

где ^ctS—коэффициент значимости гипотезы, определяемый по табл. 6 приложе­ния при р= 1—а/2 и k = n—1; а — уровень значимости гипотезы; п — число членов динамического ряда.

При этом параметр t9 определяется следующим образом:

(2. 182)

При выполнении неравенства (2.180) гипотеза об отсутствии корреляционной связи в системе (Y, t) отвергается. В противном случае указанная гипотеза не отвергается.

Выбор уравнения линии регрессии производится в соответствии с характером изменения показателей, приведенных в табл. 2.2, где U’t — средний прирост первого порядка; Ut2— средний прирост второго порядка; Yt — скользящая средняя зависимой переменной.

Показатель ……. —* ■	Характер изменения показателя	Вид кривой
ut	const	Прямая y = a + bt
Ut	Линейный	‘ Парабола второй степени у— i=a+bt+ct2
Щ2)	»	Парабола третьей степени у— =a+bt+ct2+dt3
и St	const	Экспонента у—аЬг
UtIVt	. Линейный ■	Логарифмическая парабола и=
ig ut		Модифицированная экспонен­та y = l+,abl
. ut ig — !t	»	Логистическая кривая у— 1 + +bl~at
. Ut : lg — yt	»	Кривая Томперца y=labt

Средний прирост

Ut — Ut^і + р (р + 1) (2р + 1) [фз — f 1) ijt+p+ ppt—p~ — (2р + 1) yt],

(2.183)

где р = {т — 1)/2 . . " (2.184)

т — число уровней сглаживания в интервале (число„точек сглаживания). Урав­нение (2.183) принимает вид:

при т = 3 ‘ ‘ ‘•

— yt—i — f (/^+i)/2; (2.185)

при m = 5

Ut — X — 2yt—2 — Ut—і + (//+i 4- 2у<+г)/10. (2. 186)

При m = 5 она имеет вид:

yt — (—Зу<_2+ і + 17г/^ + 2yt + i—3yt+2)- (2.188)

Наиболее простой и в то же время наиболее широко используе­мой в практике исследования эффективности систем воздушного транспорта является парная регрессия

ук = а* b*ts.

Коэффициенты регрессии рассчитываются следующим образом: b* = yjtj — nyt^I^2 ^ —(2.190)

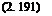а* = у— b*t.

Здесь

_

j=1 i= і

“а* ■

°У/У* •

Коэффициент значимости гипотезы ta, k определяется по табл. 6 приложения при р = 1—а/2 и k = n—2. При выполнении неравенств (2.193) гипотезы #0:а = 0 и Н0:Ь = 0 соответственно отвергаются. В противном случае указанные гипотезы не отвергаются. Интервальная оценка прогнозируемого показателя У определя­ется как (2-195) Среднее квадратичное отклонение величины уь* рассчитывает­ся по формуле

°у*к^ Су/у*

Проверка гипотезы о значимости коэффициентов регрессии аиб производится с помощью критериев

где

Пример 18. Динамический ряд индексов показателя целевой производитель­ности функционирования некоторой системы У приведен в табл. 2.3. Требуется определить прогнозируемое значение индекса показателя У на 1980 г. (t = 7). Значение показателя целевой производительности системы в базовом году М Б =200 ед.

г 1

 

Решение. 1. Производим корреляционный анализ динамического ряда индексов показателя. Необходимые вспомогательные данные сведены в табл. 2.3.

■ Таблица 2.3

В соответствии с (2.179) по данным табл. 2.2 находим;

у = 624,6/6 = 104,1; ~t = 21/6 = 3,5;
p*t = 32,50//17,50-63,76 = 32,50/33,40 = 0,973.

2. Проверяем гипотезу о значимости корреляционной связи У и t с использо­ванием критерия (2.181). Для этого вычисляем выборочную функцию (2.182) t* = 0,973/4//1 — 0,9732 «г 8,43.

Задаемся а=0,1 и по табл. 6 приложения при р=1—а/2=1—0,05 = 0,95 и — k—f>—2 = 4 определяем /о,1:4 = 2,13. В соответствии с критерием (2.181) уста­навливаем, что гипотеза о равенстве нулю коэффициента корреляции отверга­ется. Следовательно, корреляция элементов динамического ряда значима.

3. На основании качественного анализа динамического ряда приходим к вы­воду, что наиболее подходящей является прямая линия регрессии.

4. Вычисляем по формулам (2.190) и (2.191) точечные оценки коэффициен-

2218,6— 6-3,5-104,1

тов регрессии: Ь* = ——— —— б"~352—— ” = а* = ^,1 — 1.86-3,5 = 97,59.

5. Проверяем гипотезу о значимости коэффициентов регрессии а и Ъ с по­мощью критериев (2.193), для чего проводам — следующие вычисления по форму­лам ‘(2.194):

<3у/у* = {-g^— [(100,4 — 99,46)2 + (101,3— 101,32)2 + (101,8 — 103,17)2 +

+ (104,8— 105.03)2 + (106,8 — 106,89)2 + (109,5 — 108,74)2]} V2 = 0,922;
а* = {//“j” [01 — 6 -3,502)|1/2 = 1,870;

1а* ‘

6 (6— 1). 1,8702 * ‘ ‘ 0,922 1,870 /6^П — =°’221.; . 97,59 -g-ggg = 113.7; /, = 1,86/0,221 = 8,42.

	) 1/2 j = 0,858;
99

 

Задаемся а = 0,1 и вычисляем р= 1—а/2=1—0,05 = 0,95; /г = 6—2=4. Три р = 0,95 и fe=4 по табл. 6 приложения определяем to, as-, 4 = 2,13. В соответствии — с критериями (2.193) гипотеза о равенстве нулю коэффициентов регрессии а и b отвергается, т. е. оба коэффициента регрессии значимы.

6. Строим регрессионную модель прогнозирования индекса показателя’ (2.180): Уь = 97,59 — t — 1,86^

и вычисляем точечную оценку индекса показателя на 1981 .г. (th = 7): у*ы = 97,59 4-1,86-7 =110,6.

7. По формуле (2.196) находим среднеквадратичное отклонение оценки

*

У 81 ;

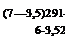
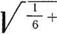= 0,858.

8. Вычисляем по формуле (2.195) интервальную оценку индекса показателя на 1981 г.:

081= 110,6 ± 2,13-0,858 = 110,6 ± 1,83, т.,е, 108,77 < у81 < 112,43.

9. Определяем точечную и интервальную оценки самого показателя произ: водительности рассматриваемой системы на 1981 г.:

М$. = 0,010gi• М0 = 1,106-200 = 221,2 ед., 1,0877-200 < М81 < 1,124-200, 217,5 < М80 < 224,8 ед/

Задача прогнозирования интересующего нас показателя с помощью регрес­сионной модели решена.

При исследовании эффективности воздушного транспорта ветре — • чаются случаи, когда возникает необходимость анализа изменения данного показателя эффективности в зависимости от изменения нескольких факторов эффективности. В таких случаях используют­ся математические модели множественной линейной регрессии.

Математическая модель множественной линейной регрессии [56]:

т

У* = «0 + 2 а*іхЧ> І = ‘ (2»197)

/ = 1

или в матричной форме

У* = а*Х, (2,198)

где Xij — независимые переменные (і = 1, т; j = 1, п) и а* (г = 1, т) — точечные оценки коэффициентов регрессии; у j — оценка зависимой переменной (/=1, п) а*—вектор оценок коэффициентов регрессии; X — матрица независи­мых переменных Хц.

Вектор точечных оценок коэффициентов регрессии определяет­ся но формуле

а* = {Х’Х)-1.Х‘У, (2,199)

*11	*12	• • ■ . *1т
•*21	*22	• • • *2 т
*п1	*я2	■ • • *ят

2*л ^jxjml 2 Xjl 2 ХМ 2 ХПхІт 2 у і 2 yjxn 2 Уіх)т

• ■ 2 хїт ■ 2 xhxІт

п

Х’Х =

]ТП

XY =

 

Матрица X’ является транспонированной матрицей X.

Среднее квадратичное отклонение точечных оценок коэффици­ентов регрессии определяется по формуле

# . * г-г—

~ °уш* * blu

ау/у* ■

7=1

Ъц—диагональный элемент матрицы (Х’Х)~1.

Проверка гипотезы о значимости коэффициентов ; регрессии (2.199) производится с помощью критерия

(2.201)

где tla, k — коэффициент значимости гипотезы, определяемый по табл. 6 при­ложения. При этом k=n—m—1.

Точечная оценка показателя У осуществляется с помощью ра­венства

у = ао — У 2 а1х*’ (2.202)

і=і

где Хік —1 значения показателей или факторов, определяющих показатель Y в момент времени th — aQ и aL— оценки коэффициента регрессии; У — точечная оценка показателя У для момента времени /»„, ;

Интервальная оценка значения. показателя У для момента вре­мени th определяется по формуле

т Ук = y*k ± *a, ftV — (2.203)

■ .к t

где — Т Vy У Хь (Х’Х)-Х*

Х/,= (xik)—матрица значений показателН’а(фактб(Шв) xif ДЛЯ МойёЙтД ‘вфеме*

НИ th.: . — • -■

Исходные данные	Расчетные данные
j	yi	*l J	хп	* у і		{уГу))2
і	10 .	2	1	10,2559:	— 0,2559	0,0655
2	12	2	2	10,8676	1,1324	1,2823
3	17	8	10	16,5324	0,4676	0,2186
4	13	2	4	12,0910	0,9090	0,8263 .
5	15	6	8	15,0520	— 0,0520	0,0270
6	10	3	4	12,2195	— 2,2195	4,9262
7	14	5	7	14,3117	— 0,3117	0,0972
8	12	3	3	11,6078	0,3922 .	0,1538
9	16	9	10	16,6609	— 0,6609	0,4368
10	18	10	11	17,4012	0,5988	0,3586
2	. 137			137,0′	0	8,3923

Пример 19. Показатель производительности некоторой системы У зависит от двух факторов Xt и Хг. В табл. 2.4 приведены исходные статистические дан­ные уj при значениях Хц, хц. Требуется определить оценку показателя У при Xih—12 и х2й = Т5.

Т а б л и ц а 2.4

Решение. 1. Принимаем уравнение регрессии

У] = aQ + aiXij + a2x2j (2.204)

а* =

и определяем точечные оценки коэффициентов а0, а і и а2. Для этого производим следующие вычисления:

Регрессионная модель получит вид:

У* = 9,3871 4- 0,1285.^ + 0,6174лг2у — (2.205)

2. Производим оценку значимости коэффициентов регрессии с помощью кри­терия (2.201). Для этого по формулам (2.204) — (2.205) проводим расчет y*j и tjj — y*j, необходимых для определения а** (2.200). Результаты расчетов све­дены в ■/абл. 2.4.

По формуле (2.200) вычисляем:

°у! у* ~ |/	10 — 2 — 1 ■8’3924^]/	8,3923 -4j — — 1.0949;
= 1,0949 1^	/2876 / — = 0,6939; = 1,0949

1,0949

Рассмотрев критерий (2.201), приходим к выводу, что гипотеза Н0 :ао=0 отвергается, а гипотезы Но’: а± = 0 и Н0 : а2 — 0 не отвергаются. Однако при «=0,3 (р=10,85) гипотеза H0:a2—0 отвергается. На основании этого делаем вывод, что переменная Xi практически не влияет на у. Положив в. модели (2.202) a j = 0 и произведя пересчет оценок коэффициентов регрессии, получим следующую модель: у*и — 9,4 + 0,7166х2£.

Следовательно, у — 9,4 + 0,7166-15 = 20,1.