СТАТИСТИЧЕСКИЕ ОЦЕНКИ ВЕРОЯТНОСТИ БЕЗОТКАЗНОЙ РАБОТЫ

Рассмотрим далее методы определения оце­нок вероятности безотказной работы и их доверительных пределов при экспоненциальном распределении отказов и различных планах испытаний.

Л Л

Функция, связывающая оценку Я, параметра К и оценку Р вероят­ности безотказной работы Р, нелинейна:

Л —XT"

Р = е. (5.69)

Поэтому, подставляя в (5.69) несмещенную оценку К, получим сме-

Л

щенную за счет нелинейности преобразования оценку Р. Смещение может быть весьма существенным в практически важном случае, ког­да надежность близка к единице из-за усечения распределения оценки

Л Л

Р на интервале (0; 1). Для определения несмещенной оценки Р при различных планах испытаний необходимо найти плотность вероятности

Л

этой оценки fp (Р) и вычислить ее математическое ожидание:

Лї[р] = j Pfp (р) dP. (5.70)

К сожалению, таким путем не удается найти конечные формулы

Л

для расчета несмещенных оценок Р. Поэтому в практических расчетах, когда нецелесообразно применять ЭВМ, остается определять оценки

Л

вероятности безотказной работы по несмещенным оценкам %, исполь­зуя формулу (5.69). Однако, зная односторонний верхний доверитель-

л л

НЫЙ Предел 5іів оценки к вычисленный С коэффициентом доверия Yl. можно совершенно точно найти односторонний нижний доверительный

Л Л

предел Р1н оценки Р с тем же коэффициентом доверия по (5.69):

Р1„ = е-"1‘Г. (5.71)

Эти соображения и заставляли так подробно анализировать форму-

л

лы для определения 7.ів при различных планах испытании. В практи-

л л

чески важном случае, когда KiBT<lO, l или Яін> 0,9, выражение (5.71) можно упростить:

PUi~l-KtDT. (5.72)

Таким образом, несмотря на трудности определения несмещенных

Л

оценок Р, используя зависимости (5.51), (5.55), (5.58), (5.63) для вы-

Л

числения Я-1В, можно с учетом (5.71) или (5.72) найти односторонний

Л

нижний доверительный предел Р1н с коэффициентом доверия Yl — для плана (п, В, Т)

Рш = ехр[— Gi_Tl й /«] • нли »1 — Gi-Tl(^) /п; (5-73)

для плана («, В, г)

Для плана (я, Б, Т) в соответствии с (5.63) и (5.71) оказывается, что

л

величина Р1н совпадает с односторонним нижним доверительным пре­делом надежности изделия, испытываемого по биномиальному плану.

л

Следовательно, величина Рін при плане (я, Б, Т), так же как и при биномиальном плане, может быть найдена по табл. П.10 для случая, когда — уі = 0,95, или с использованием приближенных зависимостей

(5.41) — (5.43), (5.45), (5.46).

Для приближенных расчетов точности оценивания вероятности безотказной работы могут быть использованы и величины средних

л л

квадратических отклонений о(Р] — оР оценок Р, найденных при раз­личных планах испытаний. Функция (5.69) является функцией случай-

А

ного аргумента К. Приближенное среднее квадратическое отклонение такой функции определяется выражением

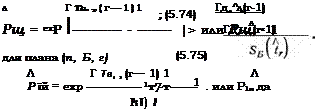— Т а

°х = Те Тр°і>

откуда

6Р/Р xKToh! K. (5.76)

Подставляя (5.50), (5.54) и (5.62) в (5.76), получим: для плана (я, В, Т)

ор/рда У(і-р)/« ;

для планов (я, В, г) и (я, Б, г)

Ор/рда-1пр/)/7 — 2 или при Р > 0,9 ор j Р да (l для плана (я, Б, Т)

/л а / -|/7Г~

ар/Рда — In Р/ у m или при

Р > 0,9 Op / Р да (1 — р) !У~т.

Рассмотрим далее некоторые приемы расчета оценок вероятности безотказной работы системы, включающей в себя конечное число k(i = 1,2, …, к) последовательно соединенных элементов. В том слу­чае, когда отказы в элементах возникают независимо и каждый отказ элемента ведет к отказу системы, несмещенная оценка вероятности безотказной работы или сокращенно надежности системы имеет вид

л /; А

Р = П Р,. (5.80)

i= 1

Л

Зная средние квадратические отклонения ст оценок Pt 1см.

* і

(5.77)—(5.79)] и линеаризуя функцию (5.80), можно найти среднее

Л

квадратическое отклонение оценки Р надежности системы:

(6-81)

Л

Если величины Pi близки к единице, то (5.81) упрощается:

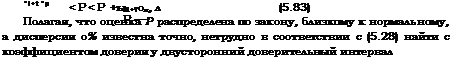(5.82)

или в соответствии с (5.29) односторонний нижний доверительный пре­дел

Рш=Р-

где н1+т и и-и — квантили нормального распределения, определяе-

2

мые по табл. П.4.

Пример 5.15. Пусть система включает в себя к = 9 последовательно сое-

А А

диненных элементов, оценки надежности которых Pt — Рг = 0,99, а средние квадратические отклонения этих оценок Ср = ар 0,001. Требуется найти

оценку надежности системы и ее двусторонний доверительный интервал с коэф­фициентом доверия у = 0,9.

В соответствии с (5.80) и (5,82) имеем:

Р = 0,99® ^0,914; ар = 0,01 1^9 ~ 0,03.

По табл. П. 4 при (1 + у)/2 = (1 + 0,9)/2 = 0,95 найдем «о,95 = 1,645 и в соот­ветствии с (5.83) получим

0,914— 1,645-0,03 < Р < 0,914+1,645-0,03, или 0,865 < Р < 0,963.

л л

При величине Р, близкой к единице, в особенности когда Р 4- + 2op > 1, распределение оценки становится явно несимметричным. В этом случае целесообразно определять только нижний доверитель-

л

ный предел РiH. Иногда удается более строго найти доверительные пре­делы для оценки вероятности безотказной работы системы, состоящей из последовательно соединенных элементов, с учетом статистических планов их испытаний. Наиболее удачные для практики результаты решения этой задачи получены в [19], которыми далее и воспользуемся.

При испытании элементов системы по плану (пь Б, Т) (і — 1, 2, k) и при отсутствии отказов во всех этих испытаниях односторонний нижний доверительный предел вероятности безотказной работы си­стемы с коэффициентом доверия у! определяется по зависимости, ана­логичной выражению (5.38):

Л Kicfe

Лн-0-Vj. (5.85)

где (Пі) min — минимальное число испытаний среди всех nt. Таким 1

образом, в рассматриваемом случае совпадают нижние доверительные пределы системы и элемента, для которого проведено наименьшее чи­сло испытаний.

Если каждый элемент системы испытывался по плану (пг, Б, Т)

Л

и наблюдалось mi отказов в каждом из яг испытаний, но надежность элементов достаточно высока и все п{>20, то отказы можно считать редкими событиями, распределенными по закону Пуассона. При этом с коэффициентом доверия Vi односторонний нижний доверительный предел оценки надежности системы

PiH = exp[—a, (m)/(n,) min ], (5.86)

1 <i<k

Л * Л Л

где m = }/П| — общее число отказов всех элементов; a,_Tl (m) —

/=і

квантиль распределения Пуассона, определяемая по табл. П.7.

Пример 5.16. Пусть при испытаниях по плану (гц, Б, Т) элементов, после-

л

довательная цепь которых составляет систему, всего наблюдалось m — 5 отка­зов, причем минимальное число испытаний для одного из элементов (иг)шіп = 50. Требуется найти односторонний нижний доверительный предел для оценки вероятности безотказной работы системы с коэффициентом доверия Ух = 0,9.

л

По табл. П.7 при 1—ух = 1 — 0,9 — 0,1 ига = 5 находим ао, і(5) = 9,275 и в соответствии с (5.86) имеем

Л —9,275/50

Р1и = е ^0,831.

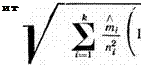
Если число отказов велико и предположение о том, что отказы как редкие события следуют закону Пуассона, становится грубым, можно

л

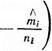для определения величин Рін использовать нормальное распределение в виде

где иъ — квантиль нормального распределения, определяемая по табл. П.4.

Пример 5.17. Пусть система состоит из трех последовательно соединенных элементов, испытываемых по плану (nit Б, Т). В результате испытаний получено

АЛА

щ — п2 = п3 = 100; nti = «2 = Щ = 10. Требуется найти односторонний ниж­ний доверительный Предел надежности системы С коэффициентом доверия Yi = = 0,9. •

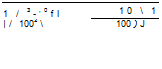По табл. П. 4 находим ыо, э = 1,282 и в соответствии с зависимостью (5.79) имеем

Заметим, что в условиях этого примера приближенное значение РГн можно найти и другим методом. В соответствии с (5.12) и (5.80) оценка надежности системы

Р = П (l— m-Jm) = (1— 10/100)3 = 0,729.

І= I

На основании (5.13) средние квадратические отклонения оценок надежнос­ти элементов

10 (l	10
юо2 У	100 )

j = 0,03.

В соответствии с (5.81) среднее квадратическое отклонение оценки надежнос­ти системы

Односторонний нижний доверительный предел оценки надежности системы с коэффициентом доверия Yi = 0,9 находим по (5.84):

Я1Н = = 0,729— 1,282 • 0,0421^ 0,675.

Таким образом, результаты получены близкие (0,693 и 0,675), однако надо отдать предпочтение формуле (5.85), так как при ее выводе было сделано меньше допущений.

При испытаниях по плану (пи Б, г) элементов, образующих по-

Л

следовательно соединенную систему, определяют наработки Sb (in) [см. (5.57)1, имеющие /^распределение. В этих условиях односторон­ний нижний доверительный предел оценки вероятности безотказной работы системы в течение времени Т с коэффициентом доверия уі опре­деляют по формуле

кН(Л = ехр [-(2r)/2[s^(/ri)]i] , (5.88)

* Л

где г = У, rr. [Sb (0-;)] —минимальная наработка до ггго

jtmmm ‘ III 1 IT

і=1 І <л<к

отказа среди всех k элементов; y2i-7. (2г) — квантиль /^ распределе­ния с 2г степенями свободы, определяемая по табл. П.8.

Пример 5.18. Пусть в результате испытаний по плану (п;, Б, г,) трех эле­ментов, составляющих последовательную цепь (систему), найдены наработки

Л

до пятого отказа (гг = 5), среди которых минимальной оказалась (/^ )]min —

= 5000 ч. Требуется найти односторонний нижний доверительный предел оцен­ки вероятности безотказной работы системы в течение Т = 50 ч с коэффициентом доверия у, = 0,9.

При г = 3 • 5 = 15 и 1 —уі — I —- 0,9 = 0,1 по табл. П.8 находим Xo, i(30) = 40,3 и, подставляя в (5.88), получим

Л —0.2015

Р1н=ехр[—50 ■ 40,3/(2 • 5000)] = е =0,818.

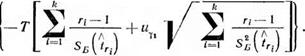Если число отказов г велико, то, так же как и для плана (пг, Б, Т), можно использовать нормальное распределение для расчета односто­роннего нижнего доверительного предела оценки вероятности безот­казной работы системы в течение времени Т:

Пример 5.19. Пусть в результате испытаний по плану (и,-, Б, п) трех эле­ментов, составляющих при последовательном соединении систему, найдены оди-

л

наковые наработки S (t ) = 5000 ч до пятого отказа (г* =5). Требуется найти

Ь Г j

односторонний нижний доверительный предел оценки вероятности безотказ­ной работы системы в течение Т — 100 ч с коэффициентом доверия = 0,9.

По табл. П.4 находим ы09 = 1,282 и в соответствии с (5.89) рассчитываем

Р1Я (Т) == ехр {— 100 [3 (5 — 1)Л5000 + 1.282 V3 (5 — I)/5000а]} =
= е-о,329 _0>720_

Эту же задачу можно решить иначе, аналогично тому, как было сделано в

Л Л

примере 5,17. По (5.56) найдем оценки 7; параметров Хг для элементов X; = (5— -0/5000 = 0,800 • 10~3 ч"1.

В соответствии с (5.69) при Т = 100 ч оценки надежности элементов Р:(Т) = — е—о,8оо — ю-®. loo ~ 0,923.

На основании (5.78) средние квадратические отклонения этих оценок ар = = — In 0,923//5=2 ж 0,0462.

По (5.80) и (5.81) рассчитываем оценку надежности системы и ее среднее квад-

Л

ратическое отклонение Р = 0,9233 « 0,786,

ср = 0,786 У 3(0,0462/0,923)2 » 0,0681.

Л

В соответствии с (5.84) имеем Рн* = 0,786 — 1,282 • 0,0681 л* 0,699.

Таким образом, и в этом случае при разных методиках расчета получены близкие результаты, среди которых нужно предпочесть найденный по более точной формуле (5.89).