ЭЛЕМЕНТОВ И НЕОПРЕДЕЛЕННОСТИ ИНФОРМАЦИИ О ПОТОКЕ ЗАЯВОК

Рассмотрим постановку задачи оптими­зации числа запасных элементов при многократном пополнении за­пасов в определенные моменты эксплуатации системы ЛК. Полагаем при этом, что задано такое число I раз пополнения запасов (см. рис. 8.1), когда выполняется условие

П = І V (8.64)

9=1

Для каждого интервала xq, в принципе, запас может быть найден решением задачи (8.61) с учетом (8.56), (8.62), (8.63). Однако в этом случае после первого интервала ть на котором будет израсходовано какое-то число элементов, новый заказ должен быть сделан с учетом остатка. Следовательно, в постановку задачи необходимо ввести ме­ханизм учета неизрасходованных элементов. При этом различают две постановки задачи:

дополнительный заказ элементов для интервала хц после завер­шения Tg_!-ro интервала эксплуатации при достоверно известном остатке rq_і запасных элементов и достаточно быстром пополнении запаса по заявке (во всяком случае, до израсходования остатка

fq-l);

планирование продолжительности интервалов xq и количества — заказываемых запасных элементов на весь период эксплуатации Тэ при заданном допустимом числе I раз подачи и удовлетворения за­явок.

Решение первой из рассмотренных задач сводится к определению величины (nq — rq_i)kN заказа для интервала xq при минимизации функции риска (8.61):

	С(Пд)=Пд (1	+ Q<z)	Л Од — ад — X, ТГ Є Czqtlq 4- л;=0
	+ Оад	СО S Х=Пд+1	ах —о ид и х—— е = min; х	(8.65)

aq = J o> (/) dt = —— J a (/) dt при tv < / < tv. (8.66)

о 9 0 v=l -*=1

В качестве исходных данных в этой задаче должны быть заданы Сзд; тд ш(/) или a(t). (8.67)

Несколько сложнее поставить вторую задачу, так как при этом необходимо дополнительно решить вопрос о прогнозировании слу­чайного количества не использованных на предыдущем интервале запасных элементов.

Обозначим через nq запас, создаваемый к началу интервала тч, а через nq — заказываемое число запасных элементов па время rq. Тогда

tl’q — nq Гg_j, * (8.68)

где rq_i — реализация случайной величины остатка Rq_.

Следовательно, на интервале rq удовлетворение заявки на запас­ной элемент со склада происходит при условии, что случайный рас­ход Xq на этом интервале не более запаса nq, т. е. при

Хд < Пд = П’ + Rq_і = П’ + (Пд_! — Xg. j)

или при

Xq -{- Xq_1 tlq Hg_j • (8.69)

Следовательно, в задаче появляется еще одна неизвестная вели­чина пд. Таким образом, для каждого интервала q = 1, 2, I не-

л

обходимо найти оптимальную продолжительность т? числа заказы­ваемых rig и размещаемых на складах п(] запасных элементов. С уче­том того, что для первого интервала число заказываемых и размещае­мых на складах элементов

п[ = пи (8.70)

общее число оптимизируемых параметров составит 3/ — 1.

Для построения функции риска потребуется распределение слу­чайной величины

Yq = Xq_l + Xq, (8.71)

определяющей расход элементов на соседних интервалах. Полагая, как и раньше, что случайная величина Xq (9= 1, 2 ……………………………………………………………………………….. /) распре­

делена по закону Пуассона с параметром

получим для суммы двух независимых случайных величин также рас­пределение Пуассона с параметром (см. [14, 68)]

cg+i + aq. (8.73)

Представим функцию риска как сумму математических ожиданий расходов на каждом из I интервалов, включающую в себя плату за: 1) заказ riq элементов; 2) хранение nq элементов; 3) повторный на интервале тд заказ элементов, если

Первая составляющая с учетом (8.59) и (8.73) принимает вид про­изведения стоимости заказа на вероятность того, что потребность сбудет меньше заказа и остатка:

Вторая составляющая мало отличается от соответствующею •члена в выражении (8.59):

тде C2q — средняя стоимость в единицу времени хранения и ТО эле­мента с учетом расхода.

а* — (^ —«5>~е

Третья составляющая принимает вид

С учетом (8.64), (8.72) — (8.76) получим функцию риска и дадим математическую постановку задачи:

^<7» Tg) —	У, I С„„; V" «=» L So xl	+
п -+С2ЛП5^	e~°Q+C3q ^ (x-nq)^ с — |= min;	(8.77)
х=0
	? . V
	°5 = J w (0 & — — J й (0 ctf; т5 6	(8.78)
	2 ^э » <7=1	(8.79)

п[ = tii’, (8.80)

9=1,2,…, 1. (8.81)

Для решения задачи (8.77) — (8.81) необходимы следующие ис­ходные данные:

1 7У, <о (/) или a (t) при 0 < / < Тэ; Clq С29; Сзд. (8.82)

Задача сводится к поиску минимума нелинейной функции от 31 — 1 неизвестных параметров при выполнении ограничений (8.78) и (8.79), заданных в виде равенств. В обычных для практики условиях функ­ция (8.77) — выпуклая и для решения задачи можно использовать обычные алгоритмы выпуклого программирования (см. [32, 63, 64]).

Заметим, что при I = 1 с учетом условия (8.80) функция риска (8.77) с точностью до постоянного множителя (Си + C2t) совпадает с (8.59) и (8.60).

Задачу (8.77) — (8.81) можно несколько упростить для случая, когда число kN элементов в системе ЛК велико и, следовательно, случайная реализация расхода элементов на интервале тд t практи­чески совпадает с математическим ожиданием расхода aq_j. При этом для всех интервалов

и’ = nq — (ng_! — %.,). (8.83)

Число неизвестных в задаче сокращается до 21, так как оптимизи­руются только значения nq и тд. Первая составляющая (8.74) функ­ции риска (8.77) упрощается:

П

Ciq [nq — (/Vi — а9_і)] ^ е 9 • (8.84)

jc=0

С учетом (8.84) функция (8.77) принимает вид

/ пд ах _а

С {tlq, Tq) = Ciq tlq {tlq-1 ~~ e 4~

(7=1 *=0

"4" Ciqtqtlq Є 4 — f — C3q (x

*=° *=Vi

а условия (8.78) — (8.81) остаются прежними. Заметим, что досто­верное знание расхода элементов на предыдущем этапе должно при­водить к некоторому уменьшению оптимальных запасов при 9=2, 3, …. I по сравнению с результатами решения более полной задачи с целевой функцией (8.77), в которой учтена дополнительная плата за неопределенность остатка rqA.

При рассмотрении задач оптимизации числа запасных элементов как при однократном, так и многократном их заказе предполагалось,
что функция изменения параметра потока заявок w(t) или a(t) в процессе эксплуатации известна достоверно. Однако на практике их можно либо прогнозировать с какой-то долей уверенности, либо оценивать статистически по результатам эксплуатации системы ЛК в течение какого-то сравнительно небольшого срока и экстраполи­ровать дальнейший предполагаемый ход функций.

Как абсолютное значение, так и вид функции to(t) во многом пред­определяют результаты решения задачи. Поэтому возможные ошибки функции (£>(t) желательно учитывать при постановке задачи. Рассмот­рим возможные варианты оценки случайной функции u)(t) или a(t) и учет неопределенности информации о ее поведении при оптимиза­ции числа запасных элементов.

Изменение функции oj(/) или a(t) в процессе эксплуатации системы ЛК можно оценить по данным отказов соответствующего элемента на различных интервалах времени.

Рассмотрим достаточно общий и важный для практики случай,, когда элемент ЛК может использоваться в двух режимах:

ожидании функционирования в течение времени эксплуатации t с периодическим контролем его состояния, техническими обслужи — ваниями, доработками и заменами, что приводит к изменению (повы­шению) его надежности;

функционирования в процессе выполнения ЛК задачи за время т, в течение которого расходуется ресурс и падает надежность элемента.

В рассматриваемой задаче нас интересует изменение o>(t, т) в каж­дый момент t процесса эксплуатации и т функционирования объекта. Характеристике a(t, т) соответствует вероятность безотказной ра­боты объекта (элемента) в течение времени т’ при условии, что объект начнет функционировать в момент t эксплуатации:

т’

— J to (t, т) dt

P{t, т’) = е 0 . (8.86)

В принципе, функция

to(t, т) = ю(/)ф(т), (8.87)

где to(t) учитывает изменение to{t, т) за счет доработок и других ме­роприятий, повышающих надежность элемента, и отражает поток заявок на элемент до начала его функционирования по данным конт­роля; ф(т) учитывает изменение to(?, т) в процессе функционирования объекта в течение времени т и отражает поток заявок на замену эле­мента с того момента, как он начал работать.

Для статистического оценивания функции ф(т) необходимы ис­пытания группы элементов в течение времени функционирования, причем все отобранные для испытания элементы должны относиться к одному периоду выпуска или времени эксплуатации. Например, если элемент в процессе функционирования невосстанавливаем, то, проведя испытания по плану [Л7, Б, Т] (см. § 5.4), можно найти А А

оценку ф(т) = ?.(т). Для заменяемого (восстанавливаемого) в про­цессе функционирования элемента по плану [N, В, Т] или [Л/, В, г)

Л Л

получим ср(т) = <в(т). В частном случае, когда поток откатов при

" Л Л

функционировании простейший, найдем оценки параметров К пли ох Поскольку в рассматриваемой задаче нас интересует в конечном счете поток заявок, то для не восстанавливаемого с начала фуикцпони-

А

рования элемента можно считать ф(т) = 1.

Для статистического оценивания функции <м(() необходимо в системе ЛК, содержащей kN элементов данного типа, фиксировать

Л

число отказов или заявок a(tj) на сравнительно небольших интерва­лах (tj, tj — f — At) времени эксплуатации. Возникает задача нахожде-

л

ния статистической оценки a(t) функции a(t) пли <л(() по наблюденным

значениям a(tj) (/ = 1,2…………… п). Будем считать, что аргумент

tj определяется достоверно, и вся неопределенность может заклю­чаться в отличии выборки kN от генеральной совокупности. Если же kN составляет всю генеральную совокупность (все элементы

Л

данного типа в системе ЛК), то будут найдены не оценки a(tj), а истинные значения a(tj), которые остается только аппроксимировать какой-либо гладкой функцией a(t), а затем использовать ее для определения величин aq в задаче (8.77) — (8.81):

^ci(t)d(t). (8.88)

о

Для случая, когда kN представляет собой выборку из генераль­ной совокупности (например, в первые годы эксплуатации не закон­чено формирование системы ЛК и число комплексов в дальнейшем будет увеличено), необходимо выбрать метод статистического оцени-

А

вания, позволяющий по данным a(tj) найти оценку функции a(t). Такая задача требует в первую очередь знания закона распределения

А

случайной величины a(tj). Если, как и раньше, предполагать, что число заявок на интервале (tj, tj + At) для /-го элемента из kN (і — ==1,2, …, kN) распределено по закону Пуассона с параметром aL(ij), то суммарный поток независимых заявок от kN элементов также рас­пределен по закону Пуассона (см. [14, 681) с параметром

kN

о(^) = 2«г(^)- (8-89)

i—i

Таким образом, по результатам эксплуатации найдены значения

A kN Л

ввНЦв|(0). (8.90)

£=1

которые представляют собой оценки параметра (8.89) закона Пуассона.

Известно, что выборочная сумма наблюдений случайной величины, распределенной по закону Пуассона, также имеет пуассоновское рас­пределение (см. [68]). Итак, установлено распределение опытных то­чек, остается принять или выбрать вид функции a{t). Обычно анали­тическую форму функции a(t) можно подобрать по характеру распо-

Л

ложения опытных точек a(tj). В частности, экспоненциальный рост вероятности безотказной работы элемента ЛК, описываемый моде­лями, рассмотренными в гл. 4, приводит обычно к экспоненциаль­ному изменению потока отказов или заявок

a(t)=a0e~at, (8.91)

где а0 и а — постоянные параметры.

Таким образом, рассматриваемая задача сводится к определению Л Л А

оценок а0, а параметров а0, а по опытным значениям a(ij), имеющим распределение Пуассона. Для решения задачи можно использовать метод максимума правдоподобия, рассмотренный в § 5.2. В соот­ветствии с (5.9) составим функцию правдоподобия, которая будет представлять собой произведение вероятностей того, что случайная величина X, распределенная по закону Пуассона с параметром a(t)„

А

примет значение a(tj), т. е.

А

і — fl вер (х = S (/,)) = П е~ . (8.92,

/=1 /-І а (tj) 1

Подставляя в (8.92) значения функции (8.91) в точках tj, по­лучим

т і П lfloe —а»е

L (а0, «) = і 1 —Ч———————— е

/=і

Перейдем к логарифмической функции правдоподобия:

In L (а0, а) = р {а (tj) (In а0 — аtj) — a0e~*tj — In [а (tj) l] J. (8.94)

Для неизвестных оценок а0 и а составим уравнения правдопо­добия:

д In L(ct0, се) ___ q# д In L (а0, а) ________ q. g

даи да

они в соответствии с (8.94) после очевидных преобразований прини­мают вид

л л

Решение уравнений (8.96) дает искомые оценки а„, а максималь­ного правдоподобия, так как можно показать, что функция (8.94) — выпуклая. Пренебрегая нелинейностью, находим искомую оценку максимального правдоподобия функции (8.91):

Л Л _а<

а (t) = с0е. (8.97)

Так же как это было сделано в § 5.9 при определении довери­тельных пределов оценки функции надежности, можно рассчитать ковариационную матрицу оценок [см. (5.175)1 и найти изменение дис­персии Dta(/)1 в каждом сечении t процесса эксплуатации. Полагая,

л

что закон распределения оценки максимального правдоподобия a(t) близок к нормальному, найдем односторонний верхний доверитель­ный предел ЭТОЙ оценки с доверительной вероятностью Yl:

«В(t. її) = a(t) + Hj_Ti У D[a{t), (8.98)

где Hi_Tl — квантиль нормального распределения, определяемая по табл. П.4.

При достаточно большом числе испытаний закон Пуассона схо­дится к нормальному, поэтому поставленную задачу определения

Л

оценки a(t) функции а(1) при большом числе kN решают не методом максимума правдоподобия, а методом наименьших квадратов (см. § 5.2). В этом случае вместо функции (8.94) в соответствии с (5.23) по­лучим выражение для поиска оценок в следующем виде:

п гл —«Ы*

2 [a(tj) — a0e ’] = min. (8.99)

/=і

Если (8.91) прологарифмировать и заменой переменной у(() = = In a(f); Уо — In «о свести к линейному уравнению

У(*) = Уо — <*t, (8.100)

Л Л Л

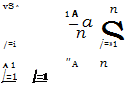то для нахождения оценок у0 — In а0 и а можно воспользоваться ко­нечными фомулами (5.202):

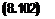л ;=1

а = Л—

Л л

где ys = In a (t j).

При использовании метода наименьших квадратов не снимаются

Л Л

трудности с расчетом изменения дисперсии Da{f) оценки a(t) функ­ции a(t), без знания которой невозможно найти искомый односто-

Л

ронний верхний доверительный предел aB(t, Yi) по зависимости (8.98).

Л гЛ і

Если в конечном итоге найдены функции a(t) и Dla(t)], то при

Л

расчете искомогодоверительного предела aB(t, yi) снова возникает за­дача нахождения оптимальной, например по критерию минимума риска, доверительной вероятности Yi — В этом случае с учетом вида и степени несимметричности функции потерь можно найти опти­мальнее значение Yi> используя результаты, полученные в § 5.8. При этом следует учитывать, что потери от ошибки в оценке вели — л л

чины a(t) возрастают в большей степени, если значение a(t) занижа­ется по сравнению с истинным из-за высокой стоимости повторного заказа и простоя ПУ. Можно рекомендовать рассчитывать оптималь­ную доверительную вероятность Y( для каждого интервала т9, на котором отыскивается оптимальное число запасных элементов при

Ад — С3д/(С1а C2q)

по зависимости (5.161)

Ті — Agl{ -(- Aq ),

соответствующей линейной несимметричной функции потерь.

Таким образом, рассмотрена процедура, позволяющая вместо до­стоверно известной функции a(t) или со(t) использовать оптимальный

Л

по критерию минимума риска верхний доверительный предел ов(/, Yi) (8.98). По существу, в задачу (8.77) — (8.81) введено дополнительное стохастическое ограничение типа

(8.105)

решаемое независимо. Следовательно, при неопределенном измене­нии параметра потока заявок задача оптимизации числа запасных элементов может быть решена в два этапа: сначала по минимуму рис­ка находят оптимальное значение верхнего одностороннего довери-

Л

тельного предела ая(і, Yi) оценки потока заявок, для чего нужно

Л Л

найти оценку функции a(t) и ее дисперсию D [«(/)]; затем решают задачу оптимизации числа запасных элементов, в которой достоверно

Л

известная функция a(t) заменяется оценкой aB(t, Yi)- При детерми­нистской постановке задачи рассматривалась функция «(/), связан­ная с параметром aq зависимостью (8.78). Если вместо «(г1) исполь-

л

зовать непосредственно функции a(t) или oB(f, Yi)> то для интервала тд среднее значение параметра потока заявок

J a(t)dt 0

или

 

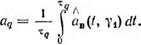(8.107)

Таким образом, полученные в предыдущем и этом параграфе ре­зультаты позволяют решить основные задачи, связанные с разработ­кой системы обеспечения системы ЛК запасными частями:

оценить и спрогнозировать переменные в процессе эксплуатации потоки заявок на элементы;

найти оптимальные периодичности и объемы заказов элементов. Решение этих задач позволяет формулирЪвать и более частные задачи: размещения запасов на системе складов, имеющих опре­деленную структуру; оптимизацию самой структуры складов; планы перемещения запасов по складам и др.