ВИБРАЦИИ

3.1. Решение задачи о колебаниях системы с распределенной массой, находящейся под воздействием дополнительных силовых

факторов

В главе 2 настоящей работы было показано, что силовые факторы, например (вес ротора), оказывают существенное влияние на поведе­ние динамической системы ротор—корпус.

В работах [142, 64] предложены новые способы подавления вибра­ции путем ступенчатого или плавного изменения жесткости ротора.

Однако адекватной модели ротора, учитывающей, например, воз­действие продольной нагрузки на поведение динамической системы ротор—корпус до настоящего времени разработано не было.

Для решения задачи применен метод конечных элементов. Алго­ритм метода использует математическую модель колебаний упругого тела без учета демпфирования и сопротивления движению, которая может быть определена в форме динамической задачи с помощью матричного дифференциального уравнения:

[М ]—у{и}+ М{и}= {F },

Эг

где [М] — матрица масс системы;

[/С] — матрица жесткости;

{и} — вектор перемещений узлов конечных элёментов;

(і1) — вектор узловых нагрузок.

Матрицы [М], [/С] и векторы { } и {F} при этом построены с учетом действия продольных нагрузок и гироскопического эффекта.

Метод конечных элементов (МКЭ) является наиболее общим прие­мом дискретизации системы с распределенными параметрами, при использовании которого дискретизируются не только инерцион­ные, но и жесткостные характеристики системы.

Описанию метода конечных элементов и способам реализации расчетов на ЭВМ с его помощью посвящена обширная литература (например, [83—85]).

Поэтому ниже приводится непосредственно решение конкретной задачи исследования свободных и вынужденных колебаний вала ро­тора, результатом которого является получение амплитудно-частот­ных характеристик, а также картины изменения внутренних силовых факторов (изгибающих моментов, продольных и поперечных сил) в процессе колебаний системы.

Пусть весь вал разбит на сечений. Тогда число конечных эле­ментов будет в каждом из которых заданы Е (модуль Юнга),

г (плотность материала вала), I (момент инерции поперечного сече­ния), F (площадь поперечного сечения).

Вал, таким образом, будет представлен в виде совокупности ба­лочных конечных элементов (КЭ).

Рассмотрим отдельно взятый конеч­ный элемент с узлами k, k+ в коорди­натной плоскости ХУ для которого оп­ределим поле перемещений, дефор­мации и работу внутренних усилий

„ (напряжений) на виртуальных переме­щениях (деформациях) (рис, 3.1).

Каждый из конечных элементов будет иметь поле перемещений, оп­

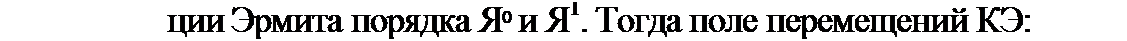ределяемое 6-ю компонентами для каждого из узлов. В качестве аппроксимирующих функций поле перемещений используем функ-

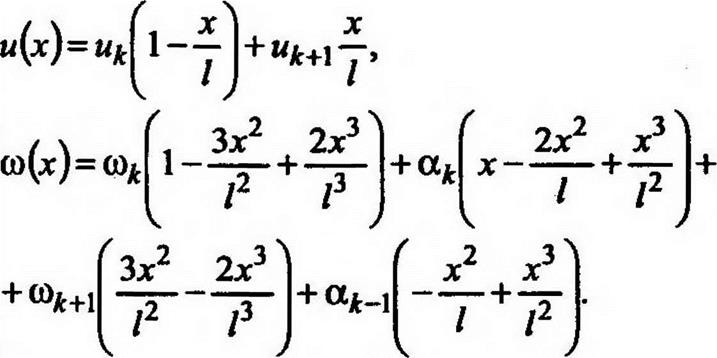(3.1)

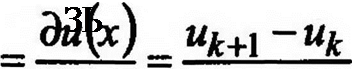Деформации КЭ запишем в виде:

Работа внутренних усилий (напряжений) на виртуальных перемещениях (деформациях):

+a*+il —г+~~jTy a*+i

+a*

(“*+1 ~uk)b(“k+l — Uk)+—[(2%k + Хк+l )&Хк + (2%* + Хк+l )Ь%к+ ]•

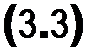
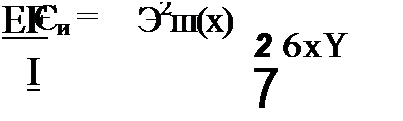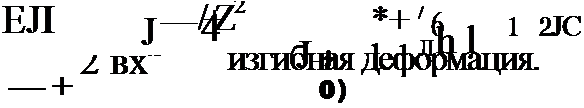J= — у-(и*+1 ~икЖ«*+і — uk)+ EJ=

xt = («>*+, — )~5~ ~ 4a* + 2a*+l;

Z Z

К

6 2a t + 2a ь.%

l 6 6a*

—"-у — — ;

zz z

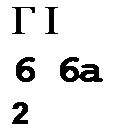+Xk+i ~ (щ+і -щ)-т~

2zt+i +x* = К-co*+i)— —ta.

Z Z

Рассмотрим процесс колебаний в плоскости XOY в обратной по­становке (т. е. вал неподвижен, а вся система нагрузок вращается относительно оси ОХ с угловой скорость со). Будем считать, что прогибы вала малы настолько, что колебания можно рассматривать независимо в координатных плоскостях XOY и XOZ. В таком случае решение задачи можно получить с помощью суперпозиции.

Система уравнений для статической задачи имеет следующий вид:

мм — м

где [К — матрица жесткости; {и} — вектор узловых перемещений; {F) — вектор узловых нагрузок.

Динамическая задача будет определяться в этом случае системой уравнений:

[*Ф>+ММ=М

где [М] — матрица масс.

Для численного решения динамической задачи с последующим со­ставлением алгоритма расчета на ПЭВМ можно воспользоваться неяв­ной (абсолютно устойчивой по времени) конечно-разностной схемой:

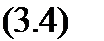Д/2 2 * 1

Так как матрица [X] из-за нелинейности колебаний зависит от времени, то с учетом приращений перемещений (м+1=м+,-м). перепишем уравнение (3.4) в окончательном виде:

МЧАц?4′ | [МІМ41

2 At2

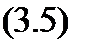ММ ЫМ£1 [д/ ка^ у

Дґ

Левая часть этого соотношения определяет систему линейных урав­нений, а правая — вектор свободных членов. Получим все компо­ненты этого уравнения.

В каждом из сечений вала заданы по 3 компонента вектора переме­щений: продольное — поперечное — И3£-1 и угол поворота Hot, где k — номер сечения, Т. е. всего 3£Я| — компонент вектора перемещений.

Очевидно, что в таком случае можно описать поле перемещений во всей области решения и, следовательно, поля деформаций и напря­жений (3.1), (3.2).

Получим матрицу жесткости /2-го конечного элемента Начальное состояние КЭ (примем /2=1 для простоты в написании индексов) и его конечное (деформированное) состояние изображены на рис. 3.2.

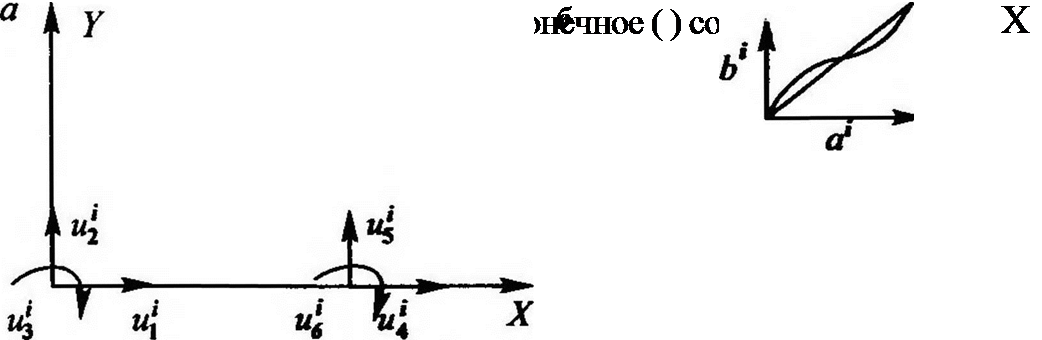Здесь і — момент времени; о1, Ы — направляющие косинусы про­дольной оси КЭ по отношению к осям соответственно.

и*1 = u[al + 1/4* = иа* + ubl

©2* = — u{bl + и12а1; ©5* = — иЪ1 + 1/5 а1.

Очевидно, что в новом (текущем, произвольном) положении КЭ продольные и и поперечные ш* смещения будут выражаться через соотношения:

Щ-1("1- "5 У + (“2 — «5 )“*]+

~^2-щУ +(«i — и4)а*]+

~Т(«2 — м5}у+ (w4+4п3 +2и6 j&/3 + + їщ ~ Щ )a2 + («5 “ "2 )*4

/ 12a / LZ. UU JU / w5 ~ M2 / З *" (M1— м4 /7Т———————- Гм3 +мб)

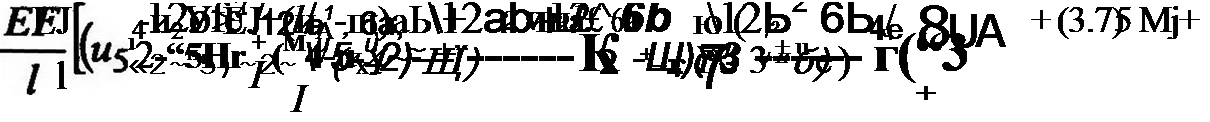Подставив (3.6) в (3.3) и опустив для простоты индекс і, получим:

EJ Г 4 6a

—I («2-«5)-

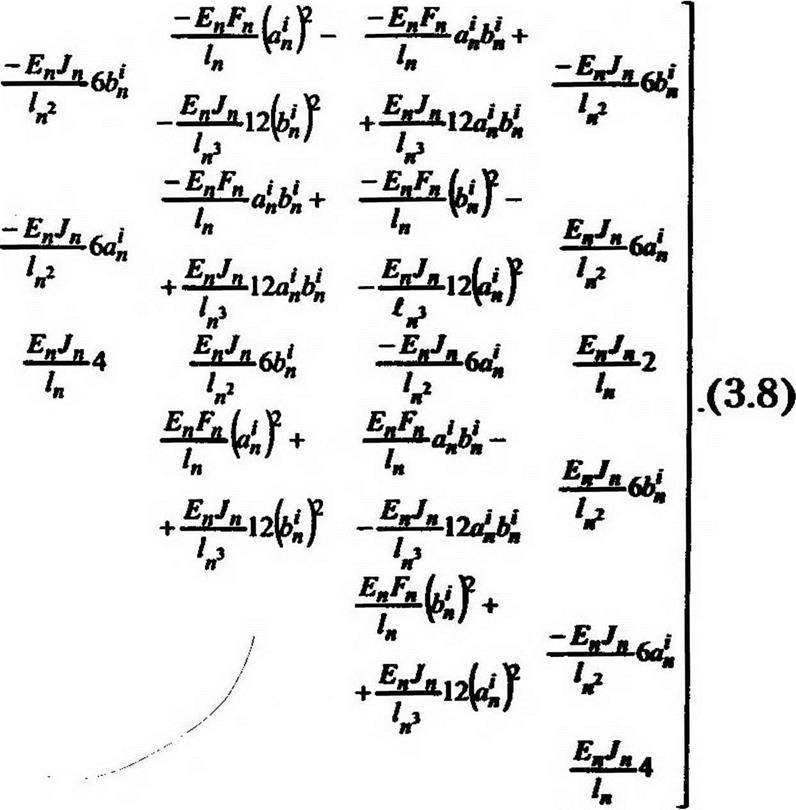Таким образом, матрица жесткости [Кп]1 п-го конечного элемен­та для момента времени і имеет следующий вид:

Для решения задачи будет использована диагональная матрица масс. В работах [83—85] рекомендуется использовать только согласованную матрицу масс, однако, в ряде случаев при решении подобных задач отмечается, что использование «сосредоточенной» или диагональной матриц масс приводит к повышению счетной устойчивости и точности.

В матрицу масс входят:

— массы собственно конечных элементов;

— массы присоединенных деталей конструкции (это метут быть, например, массы колес турбины и компрессора);

— моменты инерции «присоединенных» деталей конструкции для учета влияния гироскопических моментов на АЧХ ротора. При этом моменты инерции должны быть относительно оси, перпендикулярной плоскости ХОУ.

В таком случае масса я-го КЭ, которая равна p-F-l «разбрасывает­ся» равномерно на соседние сечения п и п+1, а остальные массовые факторы «присоединяются» к соответствующим сечениям.

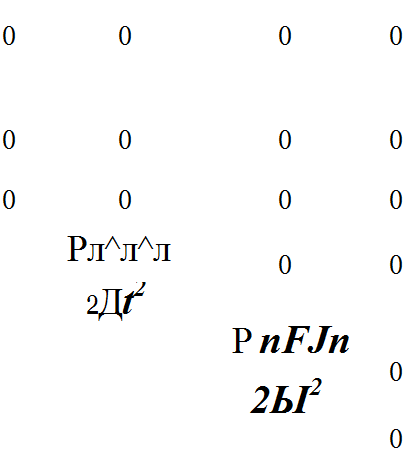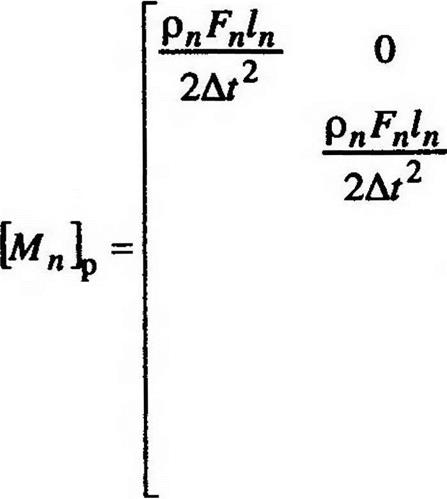Введем величину шага по времени Д£ в матрицу масс для я-го конечного элемента. Тогда для масс конечных элементов получим:

Аналогично, для k-то сечения вала для сосредоточенных масс:

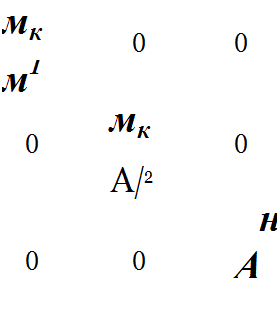(3.10)

Здесь Ml — сосредоточенная масса в k-м сечении вала;

J — соответствующий момент инерции.

Очевидно, что суммарная матрица масс [М может быть получена с помощью суммирования (3.9) и (3.10) по всем конечным элемен­там и сечениям.

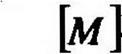=£ы+

л=1 л=1

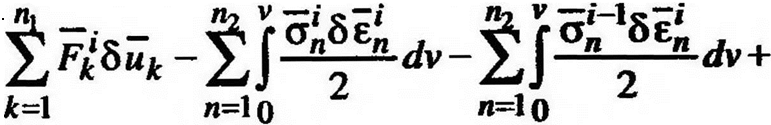Рассмотрим формирование вектора свободных членов (усилий). Далее будут рассмотрены компоненты правой части основного уравнения (3.5), которую запишем следующим образом:

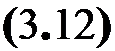А _

+ Хл*АсДі45и*.

Здесь F‘ — вектор внешних нагрузок в k-м сечении;

о’п — Ъ1п (ах, ъи ) и = є1п(єх, єи) — вектора напряжений и деформа­

ций в я-м конечном элементе соответственно;

їїя, Аи’п — вектор перемещения и его приращение для я-го КЭ;

ик, АйІ — вектор перемещения и его приращение для k-ro сечения.

Ниже будут рассмотрены и получены все компоненты выраже­ния (3.12).

При рассмотрении внешних нагрузок можно выделить 5 основных групп:

• весовые нагрузки (например, рFig — вес я-го конечного элемента);

• весовые нагрузки от сосредоточенных масс (например, М — для ненулевой сосредоточенной массы в сечении);

• поперечные нагрузки Р k для k-ro расчетного сечения;

• продольные нагрузки Pxk для k-ro расчетного сечения;

• пульсирующие нагрузки (продольные, только в двух сечениях), которые позволяют учитывать пульсации давлений на колесах тур­бины и компрессора.

В связи с обратной постановкой задачи (поле нагрузок вращается вокруг оси ОХ) первые три вида нагрузок зависят от времени, т. е. выражаются следующим образом:

р FI sin(cof), kf^gsin(a)t) Рук sin (он),

здесь со — круговая частота вращения вала.

Что касается пульсирующих продольных нагрузок (5-я группа), то они могут быть представлены в виде: Рх = р(/),

где р(£) — коэффициент, определяемый из соотношений

p(f)=5 + sin(Cc+D) (3.14)

(если р(£) < 0, то при вычислениях принимается (3(£) = 0). А, В, С, D — постоянные коэффициенты.

Суммируя все вышесказанное и соотношения (3.13) и (3.14), получим:

І Р*8й* = nFnlngsin (о/’ W “inti +

к=1 П=1 Z )

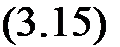+ І [(^kg + Pyk )&u3k-l sin К Pxk&u3k-2]+ X Ajk^jk^uЗД-2*

k=1

Для формирования записи этой компоненты можно воспользо­ваться соотношением (3.3), только продольную деформацию опреде­лим следующим образом:

Ф *

еі=у-1. (3.16)

Здесь /** — длина КЭ в текущем (деформированном) состоянии для момента времени і.

t*i I

(мЗл+1 иЗп-2 )^п _+ (мЗ*+1 “ и3к~2 Ж _

№*Ъ*л +хІ+і)бхІ +І? хЬ і +xi)sxWl Здесь:

Итак, рассмотрим я-й конечный элемент:

X* =-4-["Йл+і ““Зл-гЙ + Йл+г-вЗл-і)ял]-7-иЗл _7~“з(л+і):

ХІІ+1 = 75" Йл+1 _ “Зл-2 Й + Й”-1 ““Зл+гЙ]"1"/-“Зл +7“из(л+і)’

ln ln ln

г er4*)5£«(*hr

Для соотношения J о ‘и все индексы г, кроме тех, КО"

V

.

торыми обозначены а1п и Ь1п меняются на і— 1.

Виртуальная работа от внутренних усилий (напряжений) для все­го вала может быть в таком случае определена уже только с помо­щью простого суммирования по индексу я (я** 1,…, п2).

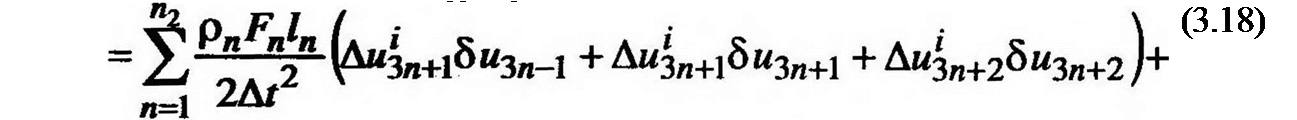
Виртуальная работа от массовых усилий может быть определена по соотношениям для матриц масс элементов (3.9), (3.10). Для вала в целом имеем:

Используя соотношения (3.5), (3.8—3.12), (3.15), (3.17) и (3.18), можно получить систему линейных (относительно приращений переме­щений) уравнений на каждом из щагов:

(3.19)

При этом следует учитывать, что при формировании правой час­ти (3.19) собираются компоненты при одинаковых buj (j — ),

причем j будет определять номер строки в векторе-столбце свобод­ных членов.

К уравнению (3.19) для его решения необходимо присоединить и начальные условия в виде

{“}={«(*)} $о}=Ш1 (3.19*)

Так как колебания вала носят установившийся характер (что, од­нако, не означает отсутствия в колебаниях переходных процессов, биений и тд), то в качестве начальных условий выбираются переме­щения, полученные при квазистатическом нагружении вала только продольными (без «пульсаций») нагрузками ^г} т. е.:

{«}={«*} (3.20)

Решение системы уравнений (3.19) с начальными условиями (3.20) целесообразно проводить методом Гаусса, адаптированным для симмет­ричных матриц с ленточной структурой (ширина ленты при этом равна 6).

Для нахождения первых (низших) частот и форм (мод) колебаний необходимо, прежде всего, составить систему линейных (относительно приращений перемещений) уравнений, описывающих процесс колебаний.

№}+[м]й=0. (3.21)

Источником нелинейности данного уравнения, как и для уравне­ния (3.4) является матрица жесткости [К (из-за коэффициентов в* , зависящих от времени).

При условии, что может быть найдена (это будет показано ниже) линейная форма записи матрицы [К], процедура определения частот и форм колебаний может быть представлена следующим образом:

а) задаемся формой колебаний (произвольный нулевой вектор {<р0} и произвольной частотой (0°, т. е. ищем решение в виде

И = (*,*) = ф(*)с05сЛ, (3.21 )

где й=й(и, со, а); Ф = ф(ф*,Ф<о>Фа)

Принимаем значение счетчика итераций і = 0;

б) определяем вектор-столбец сил инерции, т. е. вычисляем:

{9‘}=(со’)2Иф»]

в) решая задачу mV4MVM=° относительно вектора

неизвестных |ф,+1|* получаем новое приближение к форме колеба­ний;

г) новое приближение для квадрата собственной частота можно получить из соотношения:

Здесь: Mk — массовая характеристике вала в k-м сечении;

Gk — момент инерции присоединенных деталей в k-м сечении.

Получить постоянную матрицу жесткости можно, положив в ней направляющие косинусы константами, а именно: ai = 0; bi — 0. Одна­ко в таком случае невозможно будет определять частоты и формы колебаний с учетом продольных сил (и, вообще, колебания по осям X и У окажутся независимыми друг от друга).

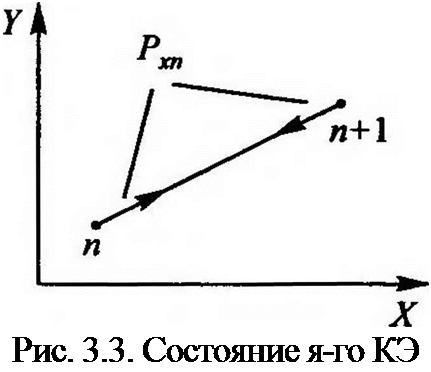
Предположим, что у нас есть (найденное, хотя бы из квазис — татического решения) распределение продольных усилий по валу ^хп = и1» п2ш Рассмотрим п-й конечный элемент (рис. 3.3).

Сила Рш в направлении оси Y будет совершать виртуальную ра­боту

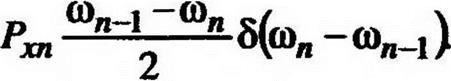(3.22*)

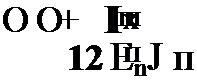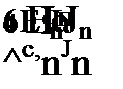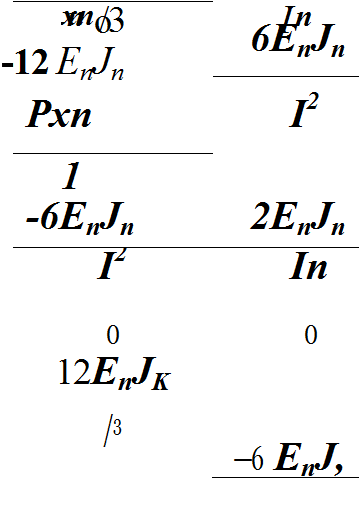Учитывая все изложенное выше, а также то, что сила (после ее выделения) является внешней, можно записать новый вариант мат­рицы жесткости, не зависящей от перемещений (или их приращений):

I

4EnJ п

I

Приведенная форма записи матриц жесткости (2.24) позволяет на­ходить собственные числа и вектора как с учетом продольных (Р * 0) сил, так и без их учета (Р — 0).

При этом матрица жесткости остается постоянной (не зависящей ни от времени t, ни от перемещений). Правда, это об­стоятельство приводит к некоторому упро­щению «физики» явления, но в рамках сде­ланных допущений (о малости перемещений, углов поворота и деформаций), практичес­ки не скажется на точности полученных ре­зультатов.

По предложенной модели разработан алгоритм решения задачи, реализованный на компьютере и имеющий следующие возможности:

— представлять вал в виде совокупности балочных конечных эле­ментов с одновременным определением графических, силовых, кине­матических и начальных условий;

— проводить анализ собственных частот и форм (мод) попереч­ных колебаний (низшие значения) валов без учета и с учетом про­дольных усилий. В последнем случае задача искусственно приводит­ся к линейной и прогибы считаются малыми;

— осуществлять численный расчет (методом конечных элементов) вынужденных продольно-поперечных колебаний валов в нелинейной постановке (с учетом углов поворота, которые, впрочем, считаются малыми). Решение системы нелинейных гиперболических уравнений при этом осуществляется с помощью конечностно-элементного пред­ставления (по координатам) с учетом линеаризации кинематических соотношений и неявной абсолютно устойчивой конечно-разностной схемы (по времени). Используемые здесь балочные конечные эле­менты допускают линейные (по длине) изменения кривизны балки. Необходимо отметить, что параметры, найденные при расчете вы­нужденных колебаний, более адекватно отвечают условиям динами­ческого нагружения, чем определенные по программе расчета соб­ственных частот и форм колебаний (это связано с приближением расчетной модели в последней к линейной, использованием более «строгого» предположения о малости прогибов, неучете продольных перемещений и связанных с последними массовых сил);

— определять параметры, характеризующие напряженно-дефор­мированное состояние балок по изменению векґора узловых переме­щений по времени. При этом имеется возможность определять как эволюции, (т. е. изменение по времени для определенного сечения вала), так и эпюры (т. е. изменение по длине вала) таких геометри­ческих и силовых факторов, как продольные и поперечные переме­щения, усилия и изгибающие моменты.

Необходимо отметить также, что имеется дополнительная возмож­ность проводить оценку статической устойчивости стержней, так как в случае действия на вал продольных сжимающих усилий, величина которых достигает критического значения, происходит потеря устойчи­вости вала. Процесс колебаний в таком случае вырождается в про­цесс апериодического отклонения вала от положения равновесия.

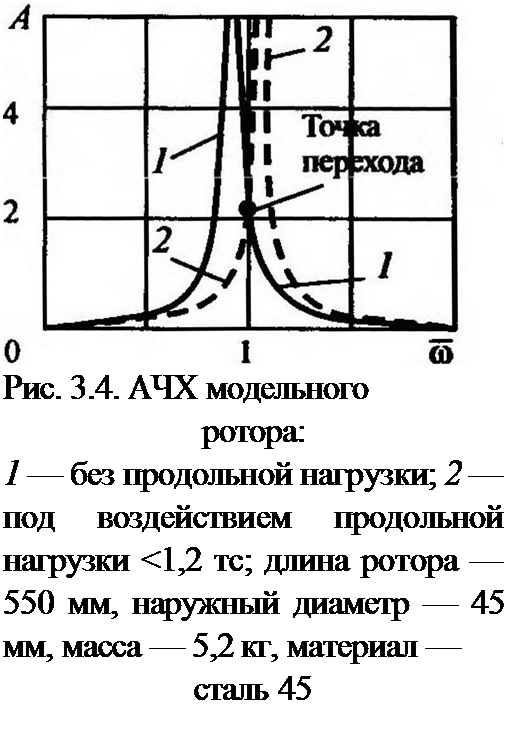
Расчетные исследования для модельного ротора (см. главу 5) дают основание сделать заключение о значительности влияния продоль­ной растягивающей нагрузки на АЧХ ротора (рис. 3.4).

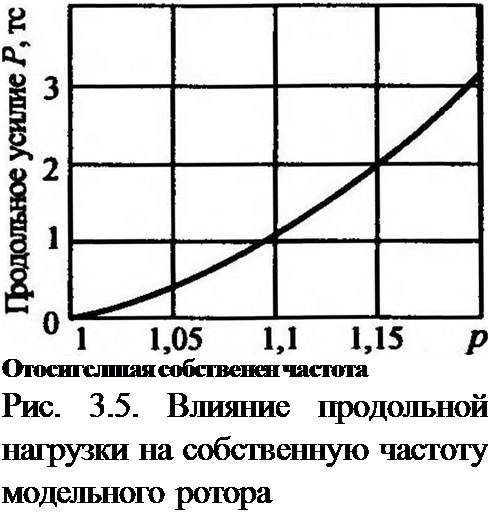
При изменении продольной нагрузки 0…3 тс (рис. 3.5) собствен­ная частота ротора изменилась на 20 %.

Экспериментальные исследования (см. главу 4) подтвердили дос­товерность расчетной методики.

Таким образом, можно сделать вывод о необходимости учета про­дольной нагрузки при определении собственных частот поперечных колебаний. Рациональное управление этим фактором может способ­ствовать смещению рабочих частот по оси абсцисс в нужную зону.

Кроме того, результаты исследований дают обоснование примене­ния для подавления вибрации разработанного автором метода [18,19], заключающегося в ступенчатом изменении жесткости ротора при его прохождении резонансной зоны путем введения и стравливания дав­ления наддува. Это позволит избежать для -«гибких» роторов даже кратковременной работы в резонансной зоне и исключает необхо­димость применения сосредоточенного демпфирования в опорах ро­тора.