МАТЕМАТИЧЕСКИЕ МОДЕЛИ РАСПРЕДЕЛЕНИЯ КОНЕЧНОЕО РЕЗУЛЬТАТА ФУНКЦИОНИРОВАНИЯ СИСТЕМЫ

Как следует из формул (2.3) и (2.13), для определения комп­лексного показателя целевой производительности системы М необ­ходимо знать функцию распределения конечного результата ее функционирования Fn{y), а для определения комплексного пока­зателя целевой надежности системы R — функции распределения конечного результата функционирования системы FB(y) и необхо­димого результата функционирования конечного результата функ­ционирования системы FB(y).

Функция распределения возможного конечного результата функ­ционирования системы

Дв(у)-Вер{Гв< у], (2.37)

где Ев—случайная величина, выражающая возможный конечный результат — функционирования — системы; у — переменная неслучайная величина, являющая­ся частной реализацией случайной величины Ув.

Если случайная величина YB дискретна, то

(у) = 2 р Шв> J= П~п, — (2.38)

У j<y

тде уj — возможное значение случайной величины Ув; Р(уі)—вероятность ве­личины Уд я — число возможных значений случайной — величины Ув.

В том случае, когда случайная величина Ув непрерывна-,

и

■ Рв {у) ~ J/в (У) dy,

о

где fa (у) —плотность распределения возможного конечного результата функци­онирования системы YB.

Функция распределения необходимого конечного результата функционирования системы Fn(y) имеет аналогичное (2.37) выра­жение ‘»

F* (</) = Вер {Г„ < у}, (2.40)

где’ Ун —случайная величина, выражающая необходимый результат функциони­рования системы; у — неслучайная переменная, являющаяся частной реализацией случайной величины Уы.

Если величина Ун дискретна, то

Fн ((/) = 2рв((/у), у=й. (2.41)

у]<у

где У і — возможное значение случайной величины Уп; Рв(Уі)—вероятность получения у у, п — число возможных значений случайной величины Ун.

В том случае, когда величина Ун непрерывна,

Fн (у) — f f*(y)dy, (2.42).

b

где fa(у)—плотность распределения необходимого конечного результата функ­ционирования системы.

Рассмотрев приведенные выше математические модели, можно заметить, что по форме математические модели функций FB(y) и FH(y) совершенно одинаковы, отличаются они лишь содержанием аргумента у. Поэтому принципы их построения должны быть так­же одинаковы.

Как известно, из теории вероятностей [15], функция F(у) явля­ется неубывающей, т. е. она обладает тем свойством, что при У2>У имеет место неравенство F(y2)^F(уг). При у = 0 функция F(y)= 0; при у = оо функция F(y) = 1. Следовательно, при ^оо имеют место неравенства

0 . /'(//) 1. (2.43)

В практике исследования случайных величин используется ряд стандартных функций распределения случайной величины, обла­дающих отмеченными выше свойствами и используемых при ре­шении практических задач.

. Биномиальное распределение. Пусть р обозначает вероятность появления события в каждом из п независимых испы­таний. Тогда вероятность того, что в п испытаниях событие поя­вится ровно у раз определяется биномиальным распределением

Ру, п-,р = СипРУ V — P)n~V’ У * > "• •

3 2412

Функция биномиального распределения

Г(У)= (2.45)

1 = 0

Математическое ожидание случайной величины, имеющей би­номиальное распределение,

х = пр. (2.46

Среднее квадратичное отклонение случайной величины, имею­щей биноминальное распределение,

а = Упр (1 — р). (2.47)

Биномиальное распределение обладает следующими свойст­ва ии:

максимум Ру — п; р достигается при у, которое определяется не­равенством

р(п+ 1)— 1 « у < р(п+ 1); • (2.48)

при п—>-оо, 0 и пр = const биномиальное распределение схо­

дится к распределению Пуассона с параметром Х = пр. Приближе­ние вполне приемлемо для п> 10 и р<0,10;

при п->-оо биномиальное распределение сходится к нормаль­ному с параметрами [х = яр и о2 = пр( 1—р). Сходимость будет хо­рошей для р = 0,5, плохой для р<1/(я+1) и р>п(п+. 1), а также вне полосы За;

рекуррентная формула

Py+V, n;p РУ^р( у + Уі)[і^р);

биномиальное распределение является дискретным; его нель­зя рассматривать как непрерывную функцию времени. Оно приме­няется тогда, когда конечные результаты классифицируются на удовлетворительные и неудовлетворительные, т. е. когда случайная величина Y имеет только два возможных значения: ух = 1 и у2 = 0.

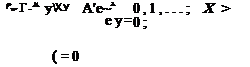Распределение Пуассона. Имеет место в тех случаях, когда на некотором интервале или площади событие с малой ве­роятностью появляется большое число раз. Основные соотношения распределения Пуассона имеют вид:

Распределение Пуассона является аппроксимацией биномиаль­ного распределения и обладает следующими свойствами:

вероятность Ру,), имеет максимальное значение для г/^(Я] (наи­большее целое число, равное или меньшее X);

для малых значений X распределение сосредоточено вблизи на­чала координат. С ростом X распределение приобретает асимптоти­ческую колоколообразпую форму. При Х>9 распределение Пуассо­на молено приближенно заменить нормальным распределением с параметрами р=А, и о2 = Х; рекурентная формула

<2’5,> если Уи Y2, …, Уп — независимые случайные величины, распре-

П

деленные по закону Пуассона, то случайная величина У = 2 Y1

7 = 1 п

распределена по закону Пуассона с параметром ^ = 2 Н — 1 і і

Равномерное распределение определяется плотностью

f(y) = !/(* — «), а<у<ь (2.52)

и функцией распределения

F (.У) = (У — &)/0-— а). (2.53)

Числовые характеристики параметров распределения р, и а оп­ределяются по формулам:

ц=(6 + а)/2; а = (6 —а) /(2/3). (2.54)

Нормальное распределение определяется плотностью

Z(i/) = (l/=/2rt)e-^-^2/2s’2 . (2.55)

и функцией распределения

F (У) =(1/о /2S) } e-^^dy.

—- оо ‘г = (У-1*)/*

Для

нормально распределенной случайной величины F имеем:

/т(2) = (і/іД2я)е“г2/2;

Ді(И = (і//2^) jV2^; (2>58)

Z

Ф с?) = (2//2л fe

о —

Значения функций fT(2), Дт(г) и Ф(г) приведены в табл. 1, 2 и 3 приложения.

Нормальное распределение обладает следующими свойствами: является колоколообразным и симметричным относительно точ­ки у = [і и имеет точки перегиба при значениях г/ = р±о; имеет од­ну моду в точке у = х, которая является также медианой; является предельным для многих распределений.

3*

Так как плотность нормального распределения отлична от нуля в интервале (—оо, — f-oo), то при его использовании математическое ожидание р, должно быть существенно больше нуля, а параметр р—Зет положительным.

Экспоненциальное распределение определяется сле­дующими плотностью

/ (у) = X е Ху, у > О и функцией распределения

F(y)= 1—е~Ч

Математическое ожидание и среднее квадратичное отклонение случайной величины, имеющей экспоненциальное распределение, равны:

Р=1Д; о=1/у% (2.61)

Экспоненциальное распределение характеризуется постоянной интенсивностью событий Я, которая является также параметром распределения. В табл. 4 приложения приведены значения функ­ции e~z, с помощью которой могут производиться расчеты вероят­ностей событий при экспоненциальном распределении.

Распределение Вей булла характеризуется трехпарамет­рической плотностью

f(x) = —(y — vf-1 ;

а

у > v, v>0, р > 0, а > 0,

где а—-параметр масштаба; |5 — параметр формы; у— параметр положения. Функция распределения Вейбулла имеет вид:

F(y) = 1 — , х > v > О, а > 0, р > 0. (2.63)

При v = 0 математическое ожидание ц и среднеквадратичное от­клонение а случайной величины, имеющей распределение Вейбул­ла, определяются так:

р = а1/рГ(1 + 1/Р); (2.64)

o=VV/fi[r(l +2/р)-{Г(1 + 1/р))2]. (2.65)

Распределение Вейбулла обладает следующими свойствами: имеет единственную моду

(/•=v + [d(l-l/P)]^, р > 1; (2.66)

при |3=1 переходит в экспоненциальное распределение.

Одним из достоинств распределения Вейбулла является разно­образие форм кривых распределения.

/(*/) =

Распределение Эрланга. При ностью и функцией распределения:

или F (*) = 1 — Р/_1 (Х. с). (2_т)

Математическое ожидание р, и среднеквадратичное отклонение о случайной величины, имеющей распределение Эрланга, вычисля­ются по формулам:

|А = /Д И o = /7/j/X (2.70)

Значения функции-

I

(2-71)

можно найти в справочниках и книгах по теории вероятности, на­пример в работе [6].

При 1=1 распределение Эрланга переходит в экспоненциальное распределение. С ростом параметра I распределение Эрланга стре­мится к нормальному распределению.. Если 020, то можно поль­зоваться табл. 1 и 2 приложения при г = (Ху — i)/y

Случайную величину Y, имеющую распределение Эрланга с параметрами X и /, можно интерпретировать как сумму взаимно независимых случайных величин Уь У2, …, И, имеющих экспонен­циальное распределение с параметром %.

Логарифмически нормальное распределение. Случайная величина У имеет логарифмически нормальное распре­деление, если InY имеет нормальное распределение с параметрами рн и (тн — Плотность и функция этого распределения имеют вид:

	/((/)-(1/°н-/2я)<р^ j	(2.72)
И		(2.73)

где Fr(z)—табличная функция. нормального распределения, значения которой приведены в табл. 2 приложения.

Математическое ожидание и среднеквадратичное ‘отклонение случайной величины Y, имеющей логарифмически нормальное рас­пределение, определяются по формулам:

u _ е(1Хн+0’5он)	(2.74)
	(2.75)
	69

При практическом использова­нии логарифмически нормального распределения следует рассматри­вать не величину У, а ее логарифм In У. В этом случае могут быть ис­пользованы табл. 1, 2 и 3 приложе­ния.

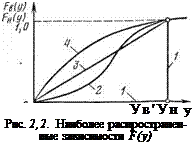Распределение Рэлея характеризуется следующими плот­ностью и функцией распределения:

/00 = 2а.-Це<-уМ у> 0;
■ f (у) = — е~(у/а)г:

• Математическое ожидание и среднеквадратичное отклонение случайной величины Y, имеющей распределение Рэлея, определя­ются так:

0,89а и а ^ 0,45а.

Как показывает опыт исследования эффективности сложных си­стем, с помощью приведенных выше стандартных распределений вероятностей могут быть найдены функции распределения конеч­ных результатов функционирования достаточно широкого класса сложных систем воздушного транспорта. Чтобы выбрать из приве­денных выше стандартных распределений наиболее подходящее для функций FB(y) и FB(y), необходимо произвести качественный анализ данной системы и конечных результатов ее функциониро­вания, выдвинуть соответствующую гипотезу, т. — е. принять одну из стандартных функций в качестве гипотетической, и произвести проверку выдвинутой гипотезы с помощью статистических методов проверки гипотезы о функции распределения случайной величины. Если же для статистической проверки выдвинутой гипотезы пет необходимых статистических данных, то принимают для практиче­ского использования выдвинутую гипотезу без статистического под­тверждения.

На основе анализа характера сложных систем воздушного тран­спорта и конечных результатов их функционирования можно уста — — новить, что наиболее характерными функциями распределения ■ возможного конечного результата являются ступенчатая 1, экспо­ненциальная 4, линейная 3 и нормальная 2 (рис. 2.2).

Ступенчатая функция распределения возможного конечного ре­зультата функционирования системы

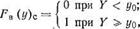(2,79)

где. у о — критическое значение аргумента у.

Она является частным случаем равномерной функции распре­деления (2.53).

Линейная функция распределения возможного зультата функционирования системы

У/Уо при 0 < Г < у0; 1 при У > у о-

Эта функция также является частным случаем равномернс функции распределения (2.53).

Экспоненциальная функция распределения возможного коне1 ного результата функционирования системы

FB(y)3 = (2.8

где а„—постоянная величина, определяемая из условия, чтобы при у=Уо им ло места приближенное равенство Рв(у0)а~. •

Нормальная функция распределения возможного конечного pi зультата функционирования системы

= ‘ (2-8:

где рв и и в—математическое ожидание и среднеквадратичное отклонение во можного конечного результата функционирования системы; FT(z)—таблична функция нормального распределения аргумента г (см. табл. 2 приложения).

В этом случае должно выполняться условие рв> ЗсГв-

Выбор одной из рассмотренных функций распределения во: можного конечного результата функционирования системы прои: водится разработчиком на основе комплексного анализа ее струї туры, внутренних и внешних связей и качества организации.

Для характеристики и математического описания функции ра< прёделения необходимого конечного результата функционировани системы FH(y), как показывают исследования, может быть исполі зована одна из тех функций, которые рекомендованы выше дл описания возможного конечного результата (ступенчатая, линеі ная, экспоненциальная или нормальная).

Ступенчатая функция распределения необходимого конечног результата функционирования системы (см. рис. 2.2)

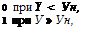
(2.8;

где ун — нормативное значение аргумента у.

Эта функция наиболее широко используется в практике иссле дования эффективности систем воздушного транспорта, хотя с тес ретической точки зрения она подвергается серьезной критике.

Линейная функция распределения необходимого конечного ре зультата функционирования. системы

Функция (2.84) используется в тех случаях, когда можно пред положить, что выполнение системой поставленной задачи возмож но и при У<уп- В этом случае на участке 0^Y<yH вероятност

выполнения системой задачи растет линейно с ростом величины конечного результата ее функционирования. Такая гипотеза не противоречит здравому смыслу, и поэтому функция (2.84) может быть использована при построении математических моделей эффек­тивности многих производственных систем воздушного транспорта. Ее достоинством является то, что она весьма удобна для практи­ческих расчетов.

Экспоненциальная функция распределения необходимого ко­нечного результата функционирования системы

Лі (у)э = 1 — е~а*у, (2.85)

где ан—постоянная величина, ‘Определяемая из условия, чтобы гари у=ун вы­полнялось условие FB(у)в~ 1.

Данная функция применима в тех случаях, когда степень объ­ективной возможности выполнения системой задачи с ростом ко­нечного результата функционирования системы растет по экспонен — ■ циальному закону, т. е. на начальном участке незначительное из­менение у приводит к существенному росту вероятности выполне­ния задачи, и для повышения вероятности выполнения системой задачи на конечном участке (см. рис. 2.2) требуется весьма суще­ственное приращение конечного результата. Экспоненциальная функция находит широкое применение в теории и практике иссле­дования эффективности воздушного транспорта.

Нормальная функция распределения необходимого конечного результата’ функционирования системы

(г/)н = Л (у — рн)/®н — (2.86)

Рассмотренные четыре вида функций распределения не исчер­пывают всех ВОЗМОЖНЫХ ВИДОВ функций FB(y) И Fitly)- Изложен­ные здесь теоретические положения должны рассматриваться как один из возможных подходов к решению поставленной задачи.