МОДЕЛИ ДЛЯ ПРОГНОЗИРОВАНИЯ ИЗМЕНЕНИЯ НАДЕЖНОСТИ ЛЕТАТЕЛЬНЫХ КОМПЛЕКСОВ ПРИ ОТРАБОТКЕ

Для аналитического описания изменения надежности ЛК в целом, его составной части, основного или сос­тавляющего элемента, происходящего во время наземной, летной отработки или эксплуатации, необходимо получить соответствующие модели роста надежности. Понятие модели весьма многогранно, но в данном случае под моделью понимают аналитическое выражение или систему зависимостей, связывающих показатель надежности с каким-либо одним аргументом и несколькими параметрами.

Чтобы получить общность результатов, будем рассматривать как единое целое некий объект, имеющий показатель надежности Р, опре­деляющий вероятность выполнения объектом какой-либо задачи во время испытания [например, вероятность безотказной работы в тече­ние заданного времени, обобщенный показатель надежности ЛК (4.1)]. Полагаем, что необходимо найти модель, описывающую изменение показателя Р от времени. Для упрощения далее назовем P(t) надеж­ностью объекта.

Обратимся теперь к исследованию причин изменения надежности. Среди рассмотренных в § 4.1 выделим главную — доработки конструк­ции и технологии производства или эксплуатации объекта. В такой постановке задача об изменении надежности объекта под действием проводимых персоналом доработок может быть отнесена к классу за­дач об изменении характеристик обучаемых или самообучающихся объектов. Действительно, есть некоторая аналогия между обучением биологических объектов (животных, человека) или кибернетических систем под действием каких-либо стимулов, вводимой эксперимента­тором (накапливаемой в процессе работы) информации и улучшением качества технического объекта под действием доработок. Дальнейший анализ покажет, что упомянутые физически отличные процессы могут иметь одинаковые формализованные схемы, как это часто случается при применении одинакового математического аппарата.

С начала 50-х годов развивается математическая теория обуче­ния, или теория стохастических моделей обучаемости, довольно полно определенная впервые в работе Р. Буша и Ф. Мостеллера [И], а позд­нее — в трудах других специалистов [31. В 60-х годах подходы, пред­ложенные в теории обучения, были использованы для получения мо­делей роста надежности при опытной отработке таких объектов, как ЛК или его составные части и элементы [40]. В 1967 г. автором были получены и исследованы более эффективные, чем предложенные в ра­боте [40], модели роста надежности ЛК в ходе отработки, а в 1974 г. —• модели роста надежности ЛК в процессе его эксплуатации (см. § 4.3 и 4.4) [4, 17, 52].

Построение моделей роста надежности объекта при опытной отра­ботке основано на анализе рекуррентного процесса, включающего в себя результаты последовательных испытаний, после которых в определенных условиях проводятся доработки, приводящие к изме­нению надежности. В зависимости от частоты и эффективности дорабо­ток рост надежности идет медленнее или быстрее. Подобная схема име­ет место и при обучении биологических объектов. Например, группу крыс пускают по Т-образному лабиринту, при повороте в лабиринте налево крысы получают корм, который стимулирует их в последую­щих опытах чаще избирать путь по левой ветви. При этом обученность крыс, оцениваемая вероятностью выбора пути к корму, будет расти от опыта к опыту, качественно, так же как надежность ЛК, «обучаемого» надежности за счет доработок.

Сформулируем два очевидных, но весьма полезных при построении моделей свойства процесса роста надежности объекта при его испыта­ниях и доработках:

1. Надежность объекта может изменяться только после проведения доработки, причем в каждой доработке она может увеличиться, умень­шиться или остаться прежней.

2. Установление предполагаемых причин отказов и их устранение доработкой возможно после любого исхода испытания.

Первое свойство очевидно и не требует комментариев, но сформу­лировано оно потому, что в ряде предлагавшихся ранее моделей (см. [40]) факт изменения надежности объекта связывайся не с доработкой, а с использованием, т. е. предполагалось, что проведение испытаний вызывает рост надежности. Второе свойство обусловлено тем, что в каждом испытании, закончившемся как успехом, так и отказом, из-за большого объема измеренных параметров накапливается информация, которую можно использовать для проведения доработок, причем эти доработки по ряду организационных причин не всегда можно провести сразу же после испытания, в котором найдена причина отказов. В боль­шинстве моделей, предложенных зарубежными специалистами, факт проведения доработки ставился в зависимость от наличия или отсут­ствия отказа в испытании. Заметим также, что второе свойство пред­полагает случайный (вероятностный), а не детерминированный харак­тер обнаружения причин отказов и их устранения, т. е. допустимы ошибки в определении причин отказов, а следовательно, возможны и доработки, не изменяющие или снижающие надежность объекта.

Таким образом, процесс опытной отработки изделия является це­ленаправленным, но случайным. Поскольку ход отработки связан с последовательностью испытаний j = 1, 2, …. п, то удобнее рассматри­вать не случайную функцию P(t), a P(j)=Pj, зависящую от номера испытания. Если бы в нашем распоряжении имелись результаты боль­шого количества опытных отработок одинаковых объектов в одинако­вых условиях, то по реализациям случайной функции Р} можно было бы легко найти ее вероятностные или статистические характе­ристики.

Сложность рассматриваемой задачи заключается в том, что прово­дится отработка только одного изделия и один раз, т. е. известна только одна реализация процесса Р-г Последний является нестационар­ным и уже тем более не эргодическим, а поэтому по одной его реали­зации оценить какие-либо параметры процесса невозможно. Попытаем­ся, используя логико-вероятностные схемы, построить такую модель

процесса, которая бы привела к получению аналитической зависимости

Р} = Р(аи a2,…,akj), (4.14)

где «і, а2, …, ак — постоянные или случайные параметры.

При этом случайная функция Р} с одной известной реализацией заменяется с точностью, определяемой качеством модели процесса, функцией случайных или неслучайных аргументов, для которой из­вестно п опытных точек, полученных в результате проведения п испы­таний. Далее (4.14) будем называть моделью роста надежности объекта.

Приступим к построению модели. Выделим произвольное у’-е звено рекуррентного процесса отработки, включающее в себя исход испыта­ния (успех или отказ) и следствие (проведение или отсутствие доработ­ки). Указанным событиям соответствуют определенные вероятности: Pj — успех в у-м испытании; яь п2 — проведения доработки после успе­ха и отказа. После любого испытания могут наступить два несовмест­ных следствия: проведение и отсутствие доработки, поэтому вероят­ность отсутствия доработки после успеха равна 1 — я*, а после отказа 1 — я2. Соответственно и приращение надежности за счет доработок после успеха составит А Ри, а после отказа — ДР2;, т. е. АР и ф АРг}.

Представим схему процесса (табл. 4.1).

Таблица 4.1 Исходы /-го испытания Вероятности исходов Следствия Вероятности следствий Вероятности успеха в (/+1)-м испытании Л1;- (успех) р, Оцу (доработка) Чр1 Pj+bPiS 1 J 012/ (нет доработки) а-ч )Р/ Pj A2j (отказ) 1 — Ps 021/ (доработка) 7t2 (I Pj) Pj+ЬРяі 02а7- (нет доработки) 0~Ч)0 ~Pj) Pj

На рис. 4.2 показана структура ветвящегося процесса отработки объекта на у’-м шаге.

Рассмотрим зависимости изменения надежности ДPi}, AP2j, так как именно они определяют конечный вид выражения Ps (4.14). В соот­ветствии с приведенным выше первым свойством процесса

АР^ ® 0; AP2J s 0. (4.15)

В [4, 11, 17, 40] показано, что наиболее удачны линейные конструк­ции, связывающие приращения надежности с достигнутой к /-му испы­танию надежностью и параметрами модели аи а2, …, ah. Такие зави­симости должны отражать повышения и понижения надежности объекта после доработки, т. е. выполнение условий (4.15), а также замедление прироста надежности с ее увеличением. В начале отработки легко обнаруживают большое количество дефектов, устранение кото­рых заметно повышает надежность, затем число выявленных причин
отказов падает, так как остаются редко проявляющиеся дефекты и надежность растет медленнее.

/-е /-е (/ + 1)-е

pllj (*Л)

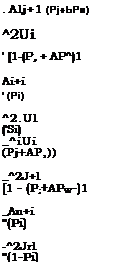испытание следствие испытание

Рис. 4.2. Ветвящийся процесс опытной отработки
объекта

С учетом сказанного в общем виде линейные операторы, определяю­щие приросты надежности, можно записать в виде

АРц = «1/(1 — Pj-і) — ЬиР,_й (4.16)

АР2] = «2/(1 — Pi-i) — b2jPj_u (4.17)

где а, ц, a2j — коэффициенты, характеризующие эффективность до­работок, т. е. уменьшение оставшейся к/-му испытанию ненадежности 1 — Р)_й bij, b2J — коэффициенты, характеризующие негативность доработок, т. е. уменьшения достигнутой к /-му испытанию надежности

Рі-1-

Заметим, что использование линейных операторов (4.16) и (4.17) дает нелинейное изменение функции Р j, так как с увеличением достиг­нутой надежности ее приращения уменьшаются даже при постоянных коэффициентах. Выражения (4.16), (4.17), логика процесса, представ­ленная табл. 4.1, и начальное значение процесса Р0 полностью описы­вают функцию Р}, которая отражает исходный случайный процесс.

Из рис. 4.2 видно, что в каждом сечении процесса существует ко­нечное, хотя иногда и очень большое, число точек, в которые могут
прийти реализации процесса. При этом каждой точке отвечает опреде­ленная вероятность попадания в нее реализации, т. е. для каждого сечения существует распределение вероятностей. Однако, как было отмечено выше, при опытной отработке ЛК или его элементов и состав­ных частей проводят одну реализацию процесса. В таком случае сле­дует различать задачи получения модели реализации процесса и его математического ожидания.

Если отработка проведена и нужно статистически оценить ее ход, то необходимо использовать модель, которая бы хорошо отражала имевшую место реализацию процесса Pj, а если нужно прогнозировать ход процесса, то удобнее использовать модель математического ожида­ния МІРj этого процесса.

Проанализируем зависимости (4.16), (4.17) и табл. 4.1, описываю­щие формализованный процесс опытной отработки. Для получения значений функции Pj в любой точке необходимо знать начальное зна­чение процесса Р0, являющееся вероятностью успеха в первом испыта­нии, а также вероятности я,, л2 и параметры сщ, a2j, Ьц, b2j, т. е.

Pj = Pj(po> ЛЬ Л2, atj, a2j, bij, b2j j). (4.18)

Таким образом, если процесс содержал число испытаний n(j — 1, 2, …, п), т. е. п экспериментальных точек, то число неизвестных па­раметров, определяющих модель, т — 3 + 4п. Из основ математи­ческой статистики известно, что для оценивания функции, содержащей т неизвестных параметров, необходимо иметь опытных точек п»т, так как дисперсия оценок параметров обратно пропорциональна ве­личине п — т и при п — т равна бесконечности. Следовательно, опе­раторы (4.16), (4.17) описывают процесс достаточно полно, но такое описание не может быть практически использовано.

Заметим, что параметры о,;-, a2J, by, b2j отражают эффективность и негативность устранения причин отказов, т. е. зависят от оснащен­ности аппаратурой и оборудованием стендов или полигонов, а также квалификации и опыта персонала, ведущего отработку. Эти категории практически не изменяются при опытной отработке одного объекта, т. е. справедливо следующее допущение:

ац = ай а2] = а2, Ьц = Ьй Ъ2} ~ Ь2. (4.19)

При этом операторы (4.16), (4.17) упрощаются:

A Pij = с,(1 — Pj_i) — biPj.6 (4.20)

A P2j = а2( 1 — TV,) — b2Pj_u (4.21)

а функция (4.18) будет зависеть от семи параметров:

Pj = Pj{P0, Jit, п2, аи «г, Ьи Ь2, /). (4.22)

Процесс (4.22) может быть промоделирован или проанализирован и для него найдено рекуррентное нелинейное выражение математиче­ского ожидания в произвольном /-м сечении (см. [11, 171).

м [PUi] = ir202 — I — [iTjCj — r2c2 + 1—^2 (o2 + 62)1 M [Pj] — f

+ [П, к + *2) — *1 (0! + &,)] A42 [Pj]. (4.23)

Для частного случая, когда

Яі(оі + £>і) = я2(а2 + Ь2), (4.24)

можно (4.23) свести к линейному уравнению, что позволяет легко найти нерекуррентную зависимость математического ожидания процесса.

Условие (4.24) выполняется тогда, когда доработки с одинаковой вероятностью я — я і = я2 следуют как после успешного, так и не­успешного испытания; в этом случае приращения надежности равны (APj = APij — = AP2j) и процесс описывается одним оператором

APi = a(l-Pj_i)~bPJ_l (4.25)

и табл. 4.2.

т- Таблица 4.2 Исходы /-го испытания Вероятности исходов Следствия Вероятности следствий Вероятности успеха в (/+1)-м испытании И и’ (отказ) Pi Ош’ (доработка) -■Pi Рі + АР і біг/ (нет доработки) (1-т) Pj Pj A.2j (отказ) 1 — Pj Ого (доработка) "(1 — Pi) Pi + АР і 0 Ї2І (нет доработки) (!-")(! — Pi) Pi

Для такой упрощенной модели математическое ожидание процес­са в соответствии с (4.23) и (4.24) описывается линейным разностным уравнением

MPj+il = яа 4- Тэта — ла 4- 1 — я (а + Ь)МР,], или

МРиА — MPj = я а — я (а + b)MPj. (4.26)

Введем обозначения

Рос — а/{а 4- Ь), (4.27)

а — я а, (4.28)

при которых (4.26) принимает вид

М [Pj+1] — М [Pj] = а — аМ [Р}/Р„. (4.29)

Величина Р0о из (4.27) является предельным значением надежности объекта, которое может быть достигнуто при числе испытаний /-*- оо. Действительно, при b — 0, т. е. когда все доработки приводят только к приросту надежности [см. выражение (4.25)], при достаточно большом числе испытаний в принципе всегда можно получить Poo = 1; при Ь Ф

Ф 0 в среднем процесс стремится к асимптотическому значению а! (а + + Ь). Величина а = тса характеризует эффективность одной доработки с учетом вероятности ее проведения.

При построении модели роста надежности предлагалось, что все причины отказов устраняются доработками. Однако и при Ра, = 1 реальный объект может иметь действительную надежность, меньшую единицы, за счет старения, выработки ресурса и других причин, что должно учитываться в расчетах методами, рассмотренными в гл. 2.

Линейное разностное уравнение (4.29) при начальном условии МР0 — Р„ имеет следующее решение (см. [11, 17]):

М [Pj] = Ра,- (Ра, — Р0)( 1 — а/Ро, У. (4.30)

Решение уравнения можно получить и другим путем.

Разделим обе части (4.29) на А/ = 1:

AAf[P,]/A/ = a(l — /Р„)М[Р,]. (4.31)

Переходя к пределу при Д/-V 0, вместо полного точного разност­ного получим приближенное дифференциальное уравнение, описываю­щее математическое ожидание процесса:

dM [PjVdj » ~а (1 — И Ра,) М IPjl (4.32)

Уравнение (4.32) при начальном условии М[Р, = Р0 имеет решение

— (Poo — Р0)е~С"Я“. (4.33)

Заметим, что переход от решения точного разностного уравнения к решению (4.33) приближенного дифференциального уравнения соот­ветствует замене

(1 — а/Ра,) «е а^Рт (4.34)

или

In (1 — а! Ра,) л* — a/Ра,.

Такая замена вызывает малые ошибки (не более 3%) при 0,8<С < с 1, что обычно выполняется в практических задачах.

Роо

Когда Poo = 1, выражения (4.30) и (4.33) упрощаются:

М IP,] = 1 — (1 — Р0) (1 — а)1, (4.35)

М IP,] =1 — (1 — Р0) е~ о/ . (4.36)

Таким образом, упрощенная модель процесса [см. выражение

(4.25) и табл. 4.3] приводит к описанию математического ожидания простой функцией от /, включающей в себя три (а, Р0, Роо) или два (а, Р0) неизвестных параметра.

Используя идею замены разностного уравнения дифференциаль­ным, найдем решение нелинейного уравнения (4.23), не прибегая к довольно сильному допущению (4.24).

Введем обозначения

(3 — ttjGj jt2а2 + 1 — я2 (а2 ~Ь Ь. г);

= »ta (о2 + b2) — ttj (a, 4- by),

при которых (4.23) записывается в виде

М [PUl] — М [Р,] = г2а2-(]-ЩМ [Р}) + аМ2 [Р,]. (4.38)

Деля обе части (4.38) на А/ = 1 и переходя к пределу при Л/->-0, получим

dM [Pj]
dj

При начальном условии ЛДР0] = Р0 дифференциальное уравнение

(4.39) имеет решение (см. [И, 17]) «-

м [Pj] = JL 4- , (4.40)

2у. 2а 1 — Сер/

еде P=V (]—№ — 4к2а2а ■ С=[2«Р0 —(1—Р) —р]/[2аР0 —(1 — — Р) + рЬ

Таким образом, решение (4.40) является приближенным [при замене разностного уравнения (4.38) дифференциальным (4.39)] выражением математического ожидания процесса роста надежности, формализо­ванного в рамках общей модели [см. (4.20), (4.21) и табл. 4.1].

В данном случае не удается оценить ошибку замены разностного уравнения дифференциальным, так как полное решение нелинейного разностного уравнения (4.34) отсутствует.

В пределе при /-> оо отношение (1 + Се?/)/(1 —Се*’) стремится к единице, поэтому предельная надежность, к которой сходится про­цесс, _

Роо » (1 — р — р)/(2а). (4.41)

Заметим также, что из (4.40) не может быть получено как частный случай при а — 0 (4.24), (4.37) решение (4.33), но при лі = я2 = 1; Яі = 0, я2 = 1 или лі = 1, я2 = 0 решение (4.40) справедливо.

Так, если доработки достоверно следуют только после успехов, т. е. Jtj = 1; я2 = 0; ал = а а2 = 0; bt = b] Ь2 = 0, то выражение

(4.40) упрощается:

М [Pj] » О. бРоо { 1 + [Р0 — (Р« — Р0) l[P0 + (Роо — Р0) Є""]} .

(4.42)

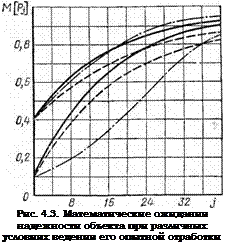
Полученные выражения (4.30), (4.33) или (4.35), (4.36), (4.40) и (4.42) описывают изменения математического ожидания процесса роста надежности при соответствующих схемах и параметрах моделей. На рис. 4.3 даны графики изменения математического ожидания MfPjl для различных моделей и исходных данных, приведенных в табл. 4.3.

Из графиков видно, что при малой начальной надежности быстрее растут кривые с высоким значением л2, причем из-за большей величины Лі эффективнее идет процесс, описываемый моделью (4.30). При боль­шем значении Р0 эти различия сглаживаются, однако на рост надежности сильнее воздейству­ет величина вероятности п. С увеличением вероятности л2 и уменьшением Я о кривые растут быстрее, так как при малом зна­чении Р0 в начале процесса чаще возникают отказы, которые слу­жат основным источником «обу­чения» объекта надежности (вы­сока вероятность л2). Аналогией таких процессов является обу­чение человека на собственных ошибках. Если же человек имеет слабые навыки выполнения ка­кой-либо работы и может их приобрести или развить только в результате удачного ее выпол­нения, то обучение пойдет мед­ленно.

Значение вероятностей л4 и л2 зависит от информативности стендо­вых или летных испытаний объектов. Большой объем телеметрической информации (данные о возможных причинах отказа и доработках объек­та) получают как при отказе, так и при успешных испытаниях, хотя неуспешные испытания несут большую информацию. Так, для летных испытаний ЛК можно принимать Лі = 0,35 0,70; л2 = 0,30 0,65,

а при стендовых испытаниях двигателей ЛА — — 0,2 — у — 0,5; л2 =

= 0,5 — г — 0,8 (см. [17]). Чем примитивнее оснащение испытаний аппа­ратурой и меньше опыт персонала, тем ниже значение вероятностей Лі и л2 и в особенности Лі. При экстенсивной отработке, когда источ-

никами информации о возможных причинах отказов служат только испытания, окончившиеся неуспешно, имеем эх, = 0. Использование же мощных измерительных комплексов и алгоритмов, позволяющих по измеренным характеристикам объекта прогнозировать возникнове­ние неисправностей, приводит в пределе к равной (я4 = ji2) и достаточ­но высокой информативности каждого испытания с любым исходом. Рассмотренные три модели (4.40), (4.30) и (4.42) охватывают основные схемы ведения опытной отработки объектов.

Таким образом, для прогнозирования процесса изменения надеж­ности ЛК или его элементов и составных частей, т. е. для описания математического ожидания процесса роста надежности, необходимо в соответствии с предполагаемым ходом процесса и данными, отражаю­щими прежний опыт отработки подобных объектов, выбрать модель и значения соответствующих параметров, после чего расчет функции МРj становится элементарным. Следует понимать, что его точность зависит от того, насколько удачно выбрана "применяемая модель и подобраны исходные данные. Значительно точнее может быть решена задача, если имеются статистические данные о ходе процесса. Методы решения такой задачи будут рассмотрены в следующем параграфе.