ВЫЧИСЛЕНИЕ ТРАЕКТОРИИ ПО ПЕРЕГРУЗКАМ

Покажем теперь, как можно получить основные кинемати­ческие параметры — линейные скорости центра тяжести само­лета и его координаты,— если известны угловые скорости (или углы) и перегрузки в функции времени 1. В § 6 и 7 мы уже видели, как можно получить углы <[>, г>, у. Поэтому будем считать, что эти углы и угловые скорости известны.

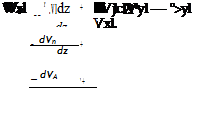Как известно из курсов_ теоретической механики, проекции ускорения центра тяжести w (или вообще любой точки твердого тела, принятого за начало связанных координат) на оси, связан­ные с твердым телом, выражаются формулами

С другой стороны, проекции вектора ускорения силы тя­жести на связанные оси равны

gx=— £ sin ft, )

gyi = — g COS» cos ч, (12.15)

&i = £cos$sinT. J

Наконец, проекции векторов ускорения центра тяжести са­молета да, ускорения силы тяжести g и перегрузки п связаны между собой в соответствии с равенством (12. 11) уравнениями

Wxl = gx—gnx,

Wyi = ёу —[ (12.16)

^ZX = gzX-gtlzl. )

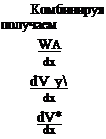уравнения (12.14), (12.15) и (12.16), легко = mzivyi — »уУа — S sin » — £Пхи

= «д-1 Va — <oltVx і — g cos b cos т—gnyl,

= <»yiVx і — ^jV/^ + ^cos&sinif—gnzl.

Эта система дифференциальных уравнений относительно Vxl, Vvu Vzi может быть проинтегрирована любым численным спосо­бом, если известны значения 0*1, у, пхи Щ9 п~ в

функции времени и известны начальные значения величин Vxu VvU Vzi. Последние известны, например, если движение началось с некоторого установившегося режима; при этом Vxi9 VyU Vz легко вычислить, зная V, а, {3.

Следует указать, что такой метод определения составляющих скорости можно применять только для сравнительно коротких промежутков времени, так как ошибки, накапливаясь при инте­грировании, могут существенно исказить результат. Поэтому при длительных промежутках времени можно этим методом пользоваться только в том случае, если желательно получить лишь качественную картину. Например, таким путем в свое время пользовались при изучении качественной картины вы­хода из штопора.

Метод очень упрощается (и уточняется) в отдельных частных случаях. Разберем, например, случай продольного движения в плоскости симметрии[17]. В этом случае <»xi = шу1 = п21= ^ = у =0 [18]

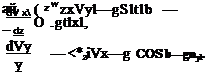и система дифференциальных уравнений приводится к весьма простому виду

Первое уравнение сводится к квадратуре

)+ f mzA-

Введем проекции вектора скорости V на земные оси Vxo, Vye, связанные с проекциями Vx и Vyl соотношениями

vx0= KriCOS&—yylsin &, Vr>,() = VJ:isin& + VJ,1cos&.

Подставляя в уравнения (12.18), получим весьма простые соотношения

— g(tlxi cos Ь — пу1 sin»),

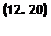dt ^

— g—fir(«,isind + «yl COS&),

dt

из которых Vxo и VyQ могут быть получены тоже простыми квад­ратурами. Зная Vxo и Vvo, можно подсчитать величины Vxt и Vy% а затем скорость V и угол атаки.

Комбинируя изложенные методы с методами, при которых скорость, высота или какие-нибудь другие параметры замеряются непосредственно, можно получить большое разнообразие мето­дов. Некоторые из них получили практическое применение.

Глава XIII