ПРИБЛИЖЕННОЕ НЕПАРАМЕТРИЧЕСКОЕ СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ

Рассмотренные выше методы статистиче­ского оценивания параметров в* распределений или параметрическо­го оценивания основаны на том, что известен вид исходного закона F(x) случайной величины X, по выборочным значениям (xj, х2,…,хп)

л

которой находят оценки 0Х. Однако на практике чаще всего досто­верно неизвестен вид распределения F(x), при этом возникает важ­ная задача проверки вида исходного закона, т. е. задача непарамет­рического оценивания.

Следует сразу же отметить, что для проверки вида распределе­ния необходимо иметь результаты по меньшей мере 40—50 незави­симых испытаний. При меньшей выборке можно оценить параметры распределения, полагая известным его вид, но проверить закон рас­пределения с достаточной достоверностью удается лишь при боль­шом числе испытаний.

Существуют различные методы проверки вида распределения. Обычно процедура сводится к проверке гипотезы о совпадении ста-

л

диетического распределения F(x) и предполагаемого теоретического F(x). Разработано большое количество критериев, по которым оце­нивается достоверность гипотез. Как правило, при большом объеме выборки (п> 100) статистическое и теоретическое распределе­ния сравниваются по нескольким критериям, что позволяет точнее принять окончательное решение.

В инженерной практике применяют простые и наглядные графиче­ские методы проверки вида распределения, при которых совпадение или несовпадение статистического и теоретического распределений оценивается визуально по их графикам. Естественно, что простота графических методов основана на отсутствии обобщенной количест­венной оценки расхождения проверяемых распределений.

Суть графических методов заключается в следующем. Для любого распределения F(x), содержащего не более двух параметров, можно подобрать такое преобразование координат р == ф(Е) и q = Щх), при котором график функции p(q), зависящий от вида распределения F(x),
превратится в прямую линию. Если в новой системе координат нанести точки статистического и теоретического распределений, то по их поло­жению легко оценить степень совпадения законов и приближенно оце­нить их параметры, так как точки теоретического распределения со­ставляют прямую, а точки статистического распределения распола­гаются около этой прямой.

Подберем преобразования координат для характерных законов распределений.

Для нормального закона с функцией распределения F(x, тх, ах) выбираем вместо исходной системы координат (F, х) новую:

р=(х — тх)/ах; q = х. (5.90)

Величина р является квантилью и нормального распределения с тх = 0 и ах — 1, т. е.

{х — тх)/ах = и или и — xlox — тх1ох. (5.91)

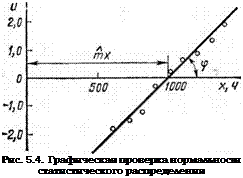Таким образом, квантили нормального распределения линейно зависят от аргумента х (рис. 5.4), причем расстояние от начала коор­динат (и, х) до точки пересе­чения прямой и(х) с осью абсцисс равно математическо­му ожиданию тх, а наклон прямой таков, что tgcp = — !ах. С другой стороны, квантиль и непосредственно связана со значением функ­ции распределения F(x)=

=ф0[(х—— ГПх)/ох] (см. табл. П.1,

П. З, П.4). Если по выбор­ке (xi, х2, xit…. хп) най — л

ТИ опытные ТОЧКИ (Ui, Xi) и нанести их на плоскость (и, х), то при нормальном рас­пределении они должны’ быть близки к прямой линии.

Л

Для построения статистического распределения F(x) или какой-либо

Л

функции р = ф(F(x)) необходимо сгруппировать выборочные значения в статистическое распределение. Для этого в выборке находят мини­мальное xmin и максимальное хгаах значения. Размах хтак — xrain де­лят на k = 6 — 20 обычно равных интервалов длиной

„ h — (xmax (5.92)

Затем определяют границы интервалов:

K= *min +2h>

Xi = X min+t/i:

*fe = *min+^ = *max’

а также величины nt, равные числу выборочных значений из (хи х2,…, хп), попавших на интервал (х’*_1> хг’), и величины т]£, равные числу выборочных значений, меньших х’;.

При этом статистическая функция распределения

F(x’i) = іу/п (і = 1, 2, …. k). (5.94)

Если число испытаний п велико, то исподрзование формул (5.19)— (5.22) требует громоздких расчетов. Тогда оценки математического ожидания и дисперсии могут быть найдены по зависимостям

Пример 5.20. Испытано 100 агрегатов до выработки ресурса. Полученные вы­борочные значения от *mj„ =500ч дохтах=1500 ч сгруппированы с учетом (5.92) и (5.93) на 10 равных интервалах длиной h = 100 ч. Частоты яг и т)г попада­ния выборочных значений на эти интервалы в зависимости от средних точек ин­тервалов х{ приведены ниже:

х[, ч…	600	700	800	900	1000	1100	1200	1300	1400	1500
Пі…	3	4	5	24	18	19	6	12	6	3
уц…	3	7	12	36	54	73	79	91	97	100

Известно, что для данных агрегатов ресурс имеет распределение, близкое к нормальному. Требуется проверить вид распределения и оценить его парамет­ры.

В соответствии с этими данными по зависимостям (5.95) находим приближен­ные с учетом группирования оценки математического ожидания и дисперсии:

тх = 550 — 0,03 + 650 — 0,04 + 750 0,05 + 850 ■ 0,24 + 950 — 0,18 +

+ 1050 — 0,19+ 1150 • 0,06+ 1250 — 0,12+ 1350 • 0,06+ 1450 • 0,03 = 998 ч;

а* =448г • 0,03 + 3482 • 0,04 + 2482 ■ 0,05+ 1482 • 0,24 + 482 • 0,18 +

+ 522 ■ 0,19+ 1522 ■ 0,06 + 2522 • 0,12 + 3522 • 0,06 + 4522 ■ 0,03 = 42696 ч2;

Л

а х~ 206,6 ч.

Л Л

Принимая полученные выше оценки тх и о,, за истинные значения тх и ах параметров нормального распределения, найдем теоретические значения кван-

Л л

тилей u-i = (Xj — тх)1ах и по табл. П. З — соответствующие им величины функ-

ции распределения F(x{) =F(U() = Ф(,(ыг). По (5.94) с учетом данных (см. с. 185)

Л

определим значения статистической функции распределения F(xi) и соответствую-

л

щие им квантили и/, используя для этого табл. П. 4 при F(xi’) = у. Результаты расчетов в зависимости от средних точек интервалов х{ приведены ниже:

xit ч. л	.. 600	700	800	900	1000
Ft…. л	. 0,030	0,070	0,120	0,360	0,540
Ui….	. 1,881	1,476	1,175	0,358	0,100
щ—-	. 1,926	1,442	0,958	0,474	0,010
Ff —	0,023	0,075	0,169	0,318	0,504 Продолжение
x’l, ч.	1100	1200	1300	1400	1500
л Fi…. л	.. 0,730	0,790	0,910	0,970	1,000
Ui…….	.. 0,613	0,806	1,341	1,881	—
Ui…….		0,978	1,462	1,946	2,430
Ft….	0,689	0,836	0,928	0,974	0,992

Л

Значения U[ и щ нанесены на рис. 5.4. Все значения иг ложатся на прямую, — , 1 998 Л —

1см. (5.9I)| и = 20б"б х — 200"g ’ Точки («;, Х[) отклоняются от этой прямой,

и величины отклонений характеризуют несовпадение опытных значений и нор-

Л /

мального распределения с параметрами тх = 998 ч и ах — 206,6 ч. Это несовпа­дение связано с ограниченностью выборки (л = 100), а также может быть выз­вано тем, что истинное распределение отличается от нормального. Визуально можно считать, что статистическое распределение удовлетворительно совпадает с нормальным.

Для графической проверки экспоненциальности распределения

с функцией

F(t) = 1 — е-м (5.96)

можно использовать следующее преобразование координат. Проло­

гарифмировав (5.96), имеем

1п—— Ц— = U. (5.97)

-F(t)

Введя новую систему координат

р — In————- и q = t, (5.98)

н 1 —F(t) 4 ‘

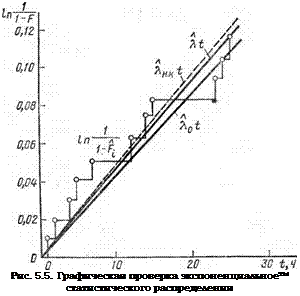
получим прямую, проходящую через начало координат с углом накло­на ф, причем tgф = 7. (рис. 5.5).

Заметим, что при плане испытаний (п, Б, Т) статистическая функция

л

распределения Ft известна до момента Т, а при плане (п, Б, г) — до

л

момента / г наступления r-го отказа. Значения статистической функции

л л л л

распределения Д — в моменты /г, /2> •••> U> ••• возникновения отказов при

планах без замены (типа Б) определяются по очевидной зависимости

Л Л Л

Ft = m(ti)lti, (5.99)

Л Л Л

где m(ti) — суммарное число отказавших изделий к моменту из п испытываемых.

Для планов с заменой отказавших элементов (типа В) значения ста­тистической функции распределения находят также по зависимо-

сти (5.99), учитывая лишь первые отказы элементов. При этом часть опытной информации не используется в процедуре проверки вида распределения.

Оценка параметра Я может быть найдена по формулам, которые при­ведены в § 5.4, применительно к конкретному плану испытаний. Кро-

Л Л 1

ме того, по т опытным точкам (у = In———— , tt) методом наимень-

1-П

л

ших квадратов нетрудно найти оценку Яи. к, которая при большом числе испытаний должна быть близка к соответствующим оценкам мак-

л

симального правдоподобия Я [см. (5.49), (5.53), (5.56), (5.59)1, так как эти оценки распределены асимтотически нормально.

В соответствии с (5.26) оценка по методу наименьших квадратов

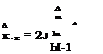
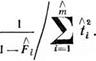(5.100)

Наконец, для закона Вейбулла (см. табл. П.1) с функцией распре­деления

F(t)= — е~}*Л (5.101)

также можно найти преобразование координат (F, t) в (р, q), при ко­тором p(q) будет прямой линией. Для этого дважды прологарифмируем выражение (5.101):

е-х/“= 1 — F(t),

получим

In [in ——= а! п/ In К. (5.102)

Следовательно, искомая замена координат имеет вид

р = in [іп — ; <7 = in t. (5.103)

Опытные точки (1п[1п—-— 1, Ыг) должны быть близки к пря-

1 -Fi(t)

мой (5.102), отвечающей теоретическому распределению, если стати-

л

стическая функция Ft{f) близка к функции распределения Вейбулла

л

(5.101). Величины Ft определяют по (5.99).

Пример 5.21. По плану (л, Б, Т) испытаны 100 агрегатов в течение Т = 25 ч.

Л Л

С точностью до 1 ч зафиксированы моменты наступления отказов /| : = 1 ч;

Л Л Л Л Л Л Л Л Л

t% ”2: /3 — 4: /4 = 5; (5 — 7, tg — 12: /7 = 14; tg = 15; /9 = 23; /jq ~ 24;

A

/tl 5= 25 4. Требуется проверить экспоненциальность закона возникновения отказов и оценить параметр X.

А А

Для перечисленных моментов Времени tl ПО (5.99) определяем величины Fj

и вычисляем значения In——— —. В качестве теоретического распределения

1 — Ft

можно принять F(t) =1 — е *, введя в это выражение вместо неизвестного

А А

истинного значения X оценку X. Для определения оценки X используем формулы (5.59) — (5.61). Суммарная наработка [см. (5.60)]

Sb(T) = 1 + 2 + 4 + 5 + 7 + 12 + 14 + 15 + 23 + 24 + 25 +• (100—

—11)25 = 2357 ч. Оценка максимального правдоподобия (5.59) X = 11/2357 г» 0,00467 ч-1. Несмещенная оценка (5.61) Х0 — (11 — 1) /2357 я* 0,00424 ч-1. Оценка по методу наименьших квадратов в соответствии с (5.100) и данными табл. 5.2

П / и

Л, V Л 1 /VU2

Хн к = V п 1п——————- — / ti = 11,381 /2390 0,00476 ч~х.

1 1 — Fi I ‘Si

Результаты расчетов представлены ниже:

Л

1 — Ft

Значения теоретической функции распределения Fj определяли по зависи-

А /.

мости Fі = 1 —е н-к<*. На рис. 5.5 приведена статистическая функция

1 Л Л

распределения в виде In——— —, а также соответствующие прямые kt, ?.01 и

1 —Ft

Л

Х-н. кб

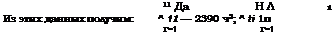
л ‘

1-^1

Совпадение статической и теоретической функции распределения, судя по рис. 5.5, можно считать хорошим.

Рассмотрим теперь процедуру проверки совпадения статистическо­го и теоретического распределений по критерию А. Н. Колмогорова.

В качестве меры расхождения А. Н. Колмогоров предложил макси­мальное значение модуля разности теоретической и статистической функций:

D = гпахІДх) — F(x)|. (5.104)

При увеличении объема выборки п вероятность неравенства D~/ri > > у стремится к пределу Р(у), который достаточно просто вычисляет­ся. Значения Р(у) приведены ниже:

у. . .	, . . 0,3	0,4	0,5	0,6	0,7	0,8
р (У) .	. . 1,000	0,997	0,964	0,864	0,711	0,544
						П родолжсние
у. .	. . . 0,9	1,0	1,1	1.2	1,3	1,4
Р(у) .	. . . 0,393	0,270	0,178	0,112	0,068	0,040

Для проверки совпадения теоретического и статистического рас-

Л

пределений вычисляют значения Ft и Ft, находят максимальную раз­ность между ними D и рассчитывают

y = D-[/Z (5.105)

По величине у находят значение Р(у)- Если эта величина достаточно велика, то гипотезу о совпадении распределений принимают.

Следует заметить, что применение критерия Колмогорова предпо­лагает точное знание теоретического распределения (вида функции и ее параметров). Если применять этот критерий для случая, когда вид распределения известен из теоретических соображений, а параметры определены по статистическим данным, то критерий дает завышенное значение Р(у), что может привести к принятию гипотезы о хорошем совпадении распределений, когда в действительности они плохо со­гласуются.

Пример 5.22. В условиях примеров 5.20 и 5.21 проверить совпадение теоре­тических и статистических распределений по критерию Колмогорова.

В условиях примера 5.20 и из данных, приведенных на с. 186, следует, что в точке X;’ -800 ч имеется максимальное расхождение (5.104): D —-10,120—0,169|= = 0,049.

В соответствии с (5.105) у — 0,049) 100 = 0,49, тогда Р(у) = 0,967, т. е. соответствие можно считать убедительным. С учетом принятых допущений мож­но принять закон нормальным.

В условиях примера 5.21 и из данных, приведенных на с. 189, имеем макси­мальное расхождение при t =7 ч — D = 0,017. В соответствии с (5.105) получим у = 0,017)^100 = 0,17, тогда Р(у) & 1,0, т. е. совпадение статистического распределения с экспоненциальным при X = 0,00476 ч-1 можно считать очень хорошим. Более строгие методы проверки вида распределения по выборкам изло­жены в специальной литературе [7, 19, 35, 38, 58, 68].