Математическая модель случайного процесса изменения параметров во времени

Как при оценке технического состояния объектов ‘ПО данным эксплуатационного контроля, так и при ана­лизе изменения надежности. по числовым показателям приходится решать одну задачу —• изучать случайные последовательности, заданные малым числом своих ■коротких реализаций, и отрабатывать методы построе­ния прогноза для них. Задачам изучения случайных последовательностей посвящено много работ советских п иностранных авторов. Для решения эксплуатационных задач достаточно результатов в области теории стацио­нарных случайных процессов, полученных А. А. Ягломом еще в 50-х годах. Более поздние работы позволяют най­ти решения и для более общих случаев. Однако практи­чески приложить методы, разработанные в теории слу­чайных процессов, часто не удается. Дело в том, что не известны необходимые для этого данные о матема­тическом ожидании ц; и среднем квадратическом откло­нении сті, о спектральной плотности f(X) или корреля­ционной функции Rp случайных процессов, образуемых результатами эксплуатационного контроля или показа­телями оперативной оценки надежности.

Корректное формальное описание наблюдаемых в реальной эксплуатации случайных процессов представ­ляет сложную проблему, которую можно решить с по­мощью специальных статистических приемов.

Если считать, что наблюдаемые в эксплуатации мно­гомерные случайные процессы имеют значения, которые при фиксированном времени подчинены распределению произвольного вида, то выписать практически, полезные решения не удается. При таких общих предположениях о характере наблюдаемого процесса не удается сформу­лировать доступные для ЭВМ алгоритмы расчетов из-за отсутствия необходимых исходных данных. Чтобы ра­зумно ограничить общность исследуемых случайных процессов в интересах эффективного ‘решения эксплуа­тационных задач, в дальнейшем принимается гауссов­ская модель изучаемых процессов, т. е. считается, что распределения всех случайных величин xh ‘(при t=eonst) подчиняются нормальному закону.

Принятое предположение (о гауссовости) хорошо обосновано относительно распределения показателей 54

надежности Хи, которые являются оценками среднего значения случайных величин или частоты события, по­лученными по выборке. О допустимости принятия нор­мального распределения значений параметров техниче­ских объектов говорилось ранее. Оба эти предположе­ния не противоречат экспериментальным данным. В каче­стве примера в табл. 2* приведены результаты провер­ки согласуемости с нормальным распределением пара­метров и показателей, о которых шла речь в предыду­щем параграфе. Для каждого показателя расчеты про­водились по двум независимым выборкам. Проверка осуществлялась с помощью критериев х2. Колмогорова

Т аблица 2 Показатель Вероятность подтвержде­ния гипотезы о нормально­сти Коэффициент асимметрии Коэффициент эксцесса £ К а £ ° Э о О? о. 2-І І&1 <о н Яс< Q. s Э II gi Sgi Я2 Sg2 Налет на отказ в по- а,42 0,18 0,34 0,4)8 -10,45 0:,7(7| лете (по авиаотрядам) 0,3:4 0!,14 0,39 0,30 Налет на неисправ- 0,37 0i,2’2 0,3)5 0,48 —0,47- 0,717 ность (по авиаотрядам) 0,7-8 0,57 0,22 —0,57 Налет на отказ в по- 0,49 0,15 0,31 0,46 0,39 0,73 лете (по типам ЛА) 0,27 0,-17 0,37 0i,26 Налет на неисправ- 0,38 0,22 0,30 0,45 —0,51 0,70 ность (по типам ЛА) 0,54 0,38 0,26 0,42 Частота вращения ро- 0,52 0,7 0,23 0,33 •—0,42 ОДІ тора авиадвигателя 0,56 0,9 0,19 0,31 Температура газов за 0,28 0,5 ■ОД 8 0,33 —0,1.7 0,64 турбиной авиадвигателя |0,44 0,5 ОД 2 —ОД 4 Тяга двигателя на 0,26 0,3 0,21 0.3-3 0,3)1 ОДІ стенде 0,31 0;,3 —од-о 0,26 Уход гироскопа авиа- 0,37 01,1-7 0,16 -0,36 —0,59 0,66 горизонта с выключен- 0,46 0,31 0,29 —Ю,42 ной коррекцией •Дрейф гиродатчика 0,3’6 0,3)7 0,23 0,33 —01,54 0;,’62 инерциальной навигаци- ■0,60- 0,46 —0,06 —0,30 онной системы Содержание железа в 0,14 ОїДОб 0,37 0,42 —.0,57 0,711 пробах масла из масло- 0,22 0,19 0,40 —0Д9 системы авиадвигателя * Цифровые данные этой и всех. последующих таблиц книги условные.

и на основании оценок коэффициентов асимметрии и эксцесса.

Из приводимых данных видно, что гипотеза о нор­мальности распределения ‘результатов измерения всех параметров и показателей надежности хорошо согласу­ется с реальностью. Чтобы убедиться, что со временем тип исходного распределения не деформируется, про­верка проводилась на основании результатов эксплуа­тационного контроля технических объектов с разной наработкой и по показателям надежности за разные го­ды. Поэтому в табл. 2 для каждого параметра или показателя х даются результаты оценки двух выборок. Можно считать, что гипотеза гаусеовости справедлива не только в одном сечении при i = const, но и для всего процесса Хи

Принятие предположения о нормальном распределе­нии случайного процесса Xi не открывает возможности непосредственного применения к задачам обработки экс­плуатационной статистики известных методов теории случайных процессов. Ведь не известны не только пара­метры, входящие в аналитические выражения характе­ристик наблюдаемых случайных процессов уц, ш, , но и сама структура этих характеристик, т. е. матема­тическая модель изучаемых процессов. Исходный ста­тистический материал, собираемый в процессе эксплуа­тации, слишком мал по объему, чтобы установить изме­нение во времени математического ожидания щ, средне­го квадратического отклонения сн и вид спектральной плотности f (X) ‘путем простого применения сглаживания экспериментальных оценок. При решении задач с малым объемом исходных данных для получения статистиче­ских характеристик наблюдаемых процессов необходимо строить оценки параметров в аналитических выражени­ях р,-, — а, /(Я) и одновременно подбирать наиболее подходящую структуру используемых аналитических вы­ражений. Приходится также следить, чтобы ошибки, появившиеся при оценке параметров в сложных анали­тических выражениях, не свели бы на нет выигрыш, ожидаемый от принятия более общей и, следовательно, более сложной модели процесса.

В задачах прогнозирования случайных процессов усложнение модели может приводить к ухудшению ка­чества прогноза. Классическим примером здесь может служить ухудшение точности экстраполяции при увели — 56

чении степени экстраполирующего полинома. Другим источником ошибки является применение для прогнози­рования значений корреляционной функции Rp наблю­даемого процесса при больших значениях аргумента р. В этом случае ошибка растет из-за недостаточно досто­верного определения корреляционной функции по реа­лизациям с малым числом точек и ухудшения обуслов­ленности решаемых систем уравнений. Таким образом, в. погоне за общностью алгоритмов не всегда целесообраз­но предлагать сложную математическую модель изучае­мых ПрОЦеССОВ Xi.

При изучении случайных процессов, описывающих, изменения значений параметров технических объемов — в эксплуатации или изменение во времени показателей надежности, удобно использовать следующую матема­тическую модель их структуры:

Х31=Цг + Щ(Ц3+£б), (2 Л )•

где Ці — математическое ожидание множества реализаций: (иногда Ці называют регрессией процесса Хі по времени); £і — случайный процесс с нулевым математическим ожиданием и еди­ничной дисперсией (приведенный к стандартному масштабу случай­ный процесс); сгі — среднее квадратическое отклонение множества реализаций от общей линии регрессии; ц%; — среднее отклонение реализации х> от общей линии регрессии Ці.

Представление (2.1) хорошо интерпретируется с точ­ки зрения инженерного анализа. Изменения во времени: математического ожидания ц,- и среднего квадратиче­ского отклонения оі, оцениваемые по всему множеству реализаций, отражают постепенное старение эксплуати­руемых объектов. Для всех номеров объектов / измене­ние ц,- и оі получается одинаковым.

Среднее отклонение значений /-й реализации Xі or общей линии регрессии:

Ч1′ =тг2 {xh — Ці), (2.2)1

и i=l

где Li — число измерений на /-Й реализации, характеризует — индивидуальные особенности начальной настройки конкретного /-го — объекта. Эта величина по времени (при изменении г) не меняется.

О виде случайного процесса £,■ не надо делать каких — либо искусственных предположений. Так, принимаемые — иногда предположения о его линейном ИЛИ МОНОТОННОМ; изменении не имеют достаточного физического обосно-

вания, поэтому не всегда справедливы в практических ситуациях. В дальнейшем будем рассматривать приве­денный случайный процесс более общего вида, который может быть представлен как сумма скользящего сред­него и авторегрессии. Такой процесс удовлетворяет уравнению (модели)

к к

2 Ре £/-6 = 2$) —0’ (2-3)

0 = 0 0=0

где Єі—случайный процесс с независимыми по і значениями (белый шум); (і])—коэффициенты авторегрессии (0=1, 2, . …Д); Рц — коэффициенты скользящего суммирования (0=’1, 2,

Математически доказано, что модели ‘(2.3) удовлет­воряет любой случайный процесс с единственным огра­ничением — значения его в данный момент не должны зависеть от значений этого процесса в будущем. Физи­чески даже трудно представить себе процесс, у которого подобное ограничение не выполнено. Доказательство общности представления (2.3) в близком для инженер­ных задач изложении можно найти в книге [13].

Принимаемая модель ‘(2.3) удобна для построения прогноза и вместе с тем является универсальной для описания процессов с реальными ограничениями, кото­рые вытекают из физической природы изменения пара­метров авиатехники в эксплуатации или показателей надежности, по времени. Процесс i в дальнейшем счи­тается стационарным. Такое предположение облегчает требования к объему необходимых исходных данных для всех практических расчетов. Но это ограничение несущественно’, потому что в модели (2.1) выделено математическое ожидание цг, которое представляется функцией времени произвольного вида. Функцией вре­мени в (2.1) считается и среднее квадратическое откло­нение 07 процесса Xi. При вычитании щ из х и вырав­нивания по о» разброса центрированного случайного процесса, т. е. для процесса вида g*=i(xi — р, г)/аг усло­вие стационарности в широком смысле сводится к тре­бованию неизменности во времени корреляционной функции Rp. Проверки неизменности корреляционной функции Rp процессов изменения параметров авиацион­ной техники показали, что во всех случаях статистиче­ский материал не противоречил гипотезе о стацйонар — ности ‘процессов Методика таких проверок дана в работе 1[25].

Введение в модели (2.1) произвольного математиче­ского ожидания ц имеет преимущество с точки зрения анализа случайных процессов изменения параметров к отличие от моделей, рассматриваемых в книге ‘[13], где в основном изучаются случайные процессы в экономике.. Выделение Ці и аппроксимация его изменения степен­ным рядом позволяют отказаться от изучения моделей: наблюдаемого процесса Xi в виде случайного процесса. со стационарными приращениями. Такое усложнение — модели — частный случай представления (2.1), так как. доказано [22], что всякий процесс со стационарными ко­нечными разностями q-то порядка может быть представ­лен в виде

5 + 2 се (0е =5+Ни 0 = 0

где ,£ — стационарный процесс се — коэффициенты аппрокси­мации p, j временным рядом.

Принятое положение о нормальном распределении, значений процесса Xi в сечениях позволяет не рассматри­вать никакие более сложные модели наблюдаемых про­цессов, чем модель (2.3). Действительно, модель более сложного вида

£г=2Ф0 Дг), (2.4)

в

где Ф (.) — функция произвольного вида,

не дает выигрыша относительно (2.3) при нормальном; распределении Xіj.

Для нормально распределенной случайной величины, всегда можно ограничиться классом линейных функций.

ФІ (•).

Модель (2.4) имеет смысл для процессов Xi с негаус­совским (например, многомодальным) распределением,, где удачным выбором функции Ф (.) можно добиться лучшего, чем в ‘(2.3) совпадения модели и реального.- процесса. Возможный здесь выигрыш достигается за. счет усложнения вычислений и резкого повышения тре­бований к объему исходных данных. Усложнение это> не всегда оправдано, так как более простая методика анализа, базирующаяся на модели (2.1), остается спра­ведливой и для негауссовских процессов. Например, по-

л

лучаемый С ее ПОМОЩЬЮ линейный Прогноз Xi. будег яаилучшим в смысле минимизации среднего квадрати­ческого отклонения от прогнозируемого значения. Нели­нейный прогноз может быть лучше только с точки зре­ния минимизации вероятности ошибки предсказания. При нормальном распределении xh линейный прогноз обеспечивает минимальное среднее квадратическое от­клонение и минимальную вероятность ошибки.

Приведенный процесс li, подчиняющийся соотноше­нию (2.3), имеет спектральную плотность f(%), которую с любой степенью точности можно аппроксимировать дробно-рациональной функцией

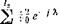б

2 f

0=0

‘•Во многих практических задачах можно ограничить­ся более простым представлением для спектральной плотности, чем (2.5). У случайного процесса £,■ со спект­ральной плотностью (2.5) и соответствующей ей мо­делью (2.3) значение в любой фиксированный момент времени связано статистически с бесконечным числом предыдущих значений. Такой процесс физически пред­ставить себе гораздо труднее, чем процесс, у которого значение в і-й момент зависит лишь от конечного (пусть большого) числа предыдущих значений при

® = 1, 2,…, I. Поэтому потребности практики чаще всего удовлетворяет более простая модель

V

«/ = 2 Ре о+ «/. — (2-6)

е=1

получающаяся из (2.3), если считать в ней /2 = 0, рг0 “= 1.

У процесса, соответствующего этой модели, зави­сит от конечного числа g„-_o. Такой процесс называют процессом с «конечной памятью» или авторегрессион­ным. Модели (2.6) соответствует более простое, чем

(2.5)

, представление спектральной плотности:

Завершая описание принятой математической моде­ли наблюдаемых процессов, отметим, что она применима при изучении одномерных процессов и для независимых 60

составляющих многомерного процесса. Вместе с тем каждую составляющую стационарного многомерного гауссовского процесса можно представить как линейную комбинацию независимых между собой случайных про­цессов fij имеющих нормальное распределение в сече­ниях. Процессы fi можно изучать и прогнозировать как одномерные в рамках модели >(2.1). Прогноз же исход­ного многомерного процесса xt будет получаться как ли­нейная комбинация прогнозов fi. Методика представ­ления составляющих M-мерного случайного процесса как линейной комбинации независимых между собой составляющих другого многомерного процесса рассмат­ривается в гл. 3. Существенную роль в этой методике играет изучение матрицы корреляций 2 значений от­дельных составляющих исходного случайного процесса. Поскольку матрица корреляций 2 для стационарных процессов не меняется во времени, в дальнейшем можно ограничиться ее изучением в любом фиксированном сечении t=const.