Массы

В большинстве случаев современные виброзащитпые системы яв­ляются пространственными. Специфика работы машин, устанав­ливаемых на виброзащитпые системы пространственного типа, тако­ва, что их центр масс, как правило, совершает связные гармонические колебания. В работах [131, 69J показано, что связные гармонические движения вибратора в механических системах с конструкционным демпфированием приводят к существенному изменению формы гис­терезиса и позволяют упростить представление дифференциальных уравнений колебания этих систем.

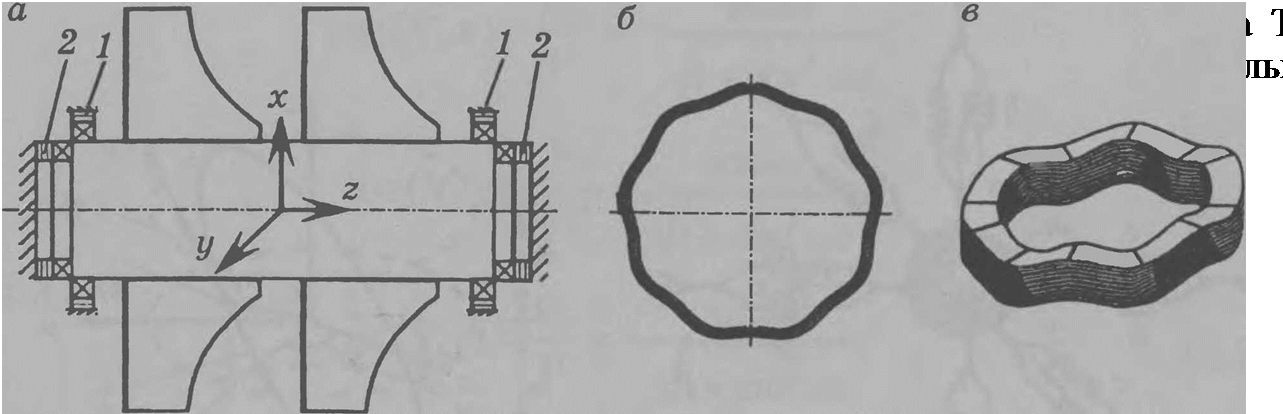
В указанных работах рассмотрены лишь случаи плоских прецес­сионных движений. Но в аэрокосмической технике колебания рото­ров турбопасоспых агрегатов являются трехмерными. Так, например, ротор ТНА 2-й ступени ЖРД «Энергия» установлен на простран­ственной виброзащитпой системе, состоящей из системы мпогослой-

пых гофрированных демпферов [70] с радиальным и осевым гофри­рованием пакетов (рис. 2.36).

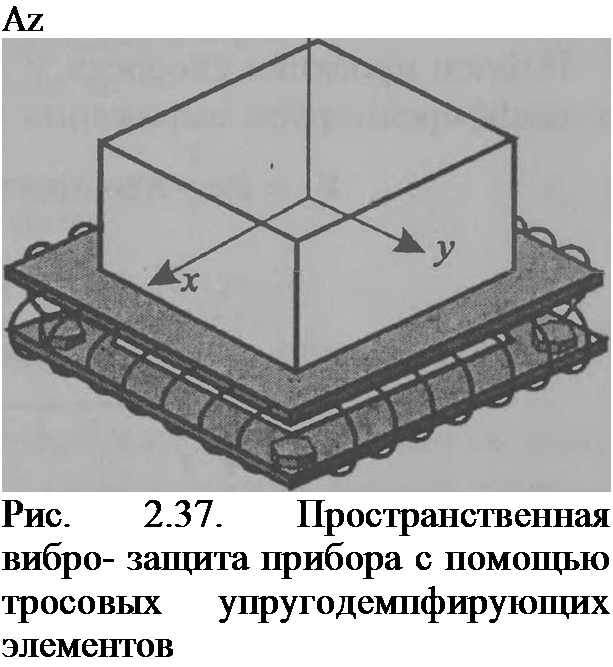
Приборное оборудование, устанавливаемое на вибрирующих кор­пусах двигателей летательных аппаратов, а в общем случае узлы и агре­гаты ТС подвержены также пространственным колебаниям (рис. 2.37).

В настоящей работе делается попытка рассмотрения особенностей формирования гистерезиса при связных гармонических колебаниях объекта виброзащиты в направлении трех взаимно-перпендикуляр­ных осей.

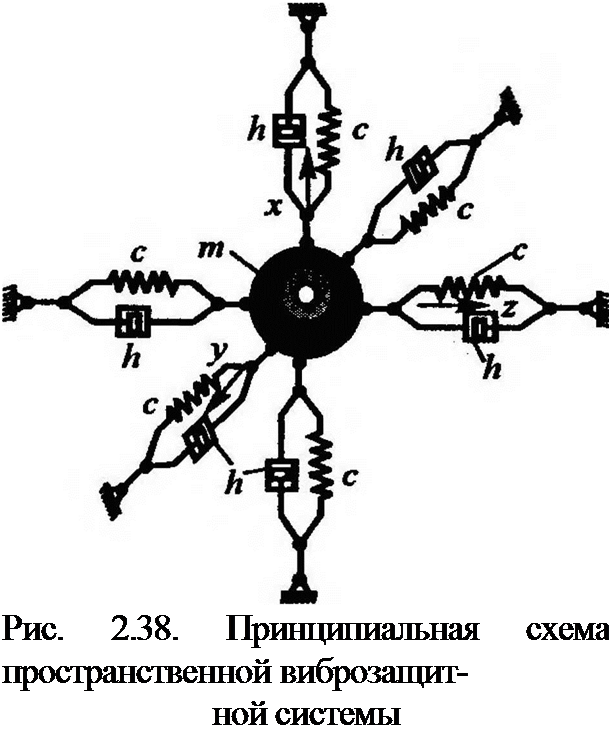
Пусть в произвольный мо­мент времени t центр масс объек­та, расположенного па простран­ственной упругодемпфирующей подвеске (рис. 2.38) движется по замкнутой траектории с закона­ми движения в виде:

х = Acos со^,

у = Asm со£; (2.11)

z = Acos <at.

Траектория вибратора при та­ких законах движения имеет вид наклоненного эллипса, причем проекции этого эллипса на плос-

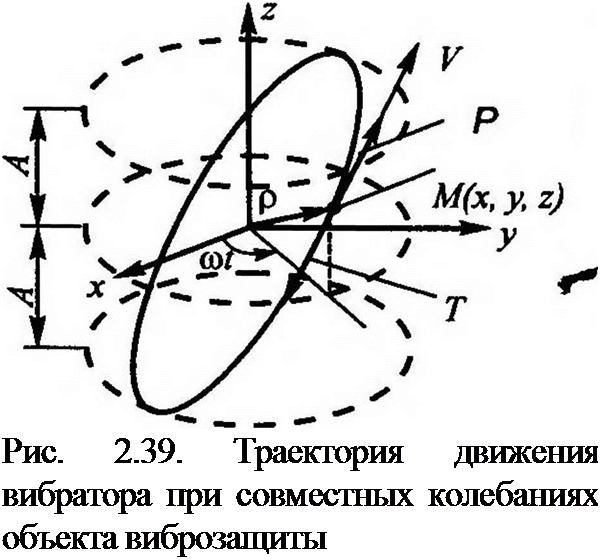кости хОу и zOy являются окружностями, а на плоскость zOx — прямая, наклоненная к оси Ох под углом 45° (рис. 2.39).

Рассмотрим вначале случай, когда при движении точки М по траектории на нее действуют только внешняя сила Р и сила сопро­тивления демпфирующего устройства Т.

Как известно, сопротивление среды всегда направлено против дви­жения, т. е. в сторону, противоположную вектору скорости V. Будем также считать, что модуль силы сопротивления Т не зависит от ско­рости движения и является постоянным, т. е. Т =const.

Найдем проекции скорости V точки М на оси координат, для чего продифференцируем выражения (2.11) по времени

Vx=x = -/Uosino*; Vy = у — Лео cos со/;

Vz — ‘z— — Асо sin со/. (2.12)

Модуль вектора скорости определится в виде

V = — Jv? + Vy + Vz2 = + sin 2<of. (2.13)

Используя выражения (2.12) и (2.13), можно найти направляю­щие косинусы вектора V для расчета в дальнейшем проекций силы трения (неупругого сопротивления) на координатные оси:

(2.14)

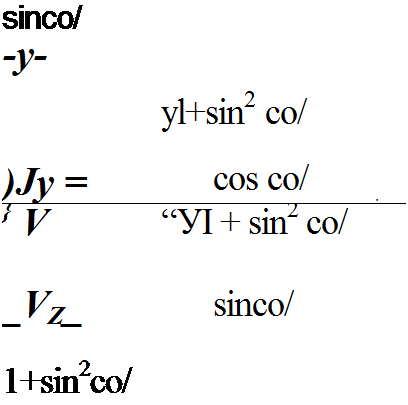(2.15)

(2.16)

Поскольку в любой момент времени модули сил равны друг другу, а линия действия сил РиТ совпадает с направлением вектора V, найдем проекции силы Р на оси координат:

Рх—Т cos( V, д:) = —Т

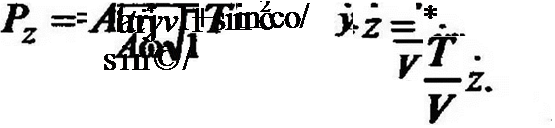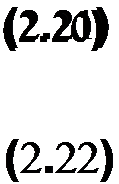Умножив и разделив выражения (2.17)—(2.19) на Лю, получим

Выражения (2.20)—(2.22) показывают, что при постоянном модуле силы неупругого сопротивления Т и гармонических законах движения вибратора защищаемого объекта проекции внешней силы Р^ Ру, Pz и равные им, но противоположные но направлению проекции силы сопротивления Тг Ту, Тг зависят от скорости движения точки М.

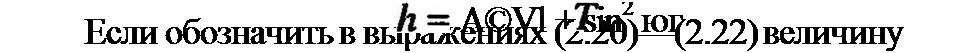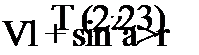через к:

то проекции сил Рх, Ру, Р2 можно представить в привычном для линейно-вязкого трения виде:

Px=hx; Ру = hy;pz=hz. (2.24)

Напомним, что в работе рассматривается вопрос о математичес­ком описании гистерезиса в пространственных виброзащитных сис­темах с сухим трением!

Если скорость V и сила сопротивления Т не зависят от координат и времени, то коэффициент демпфирования h = const, в противном случае, как это следует из выражения (2.23), коэффициент h —f(T, V) =/(х, у, z, V).

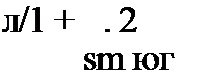.Найдем зависимости между Рх и х, Ру и г/, а также Pz и г. Для этого сделаем следующие преобразования. Из выражений (2.11) и (2.20) найдем

Возведем правые и левые части выражений (2.25) в квадрат и сложим почленно:

р2 sin*’ cor + cos2 cor = —у (1+sin 2 cor) +

2

=1.

Если обозначить

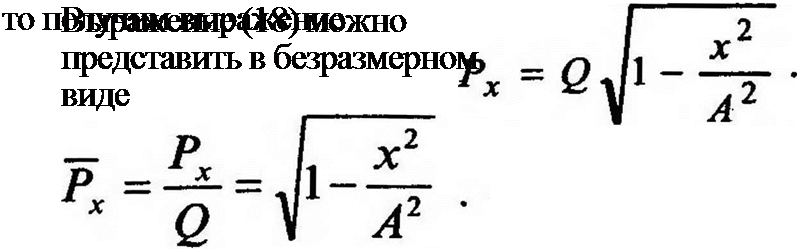-i-(l + sin2 cor) = Q2, (2.27)

Зависимость р = f(xl А) является точным эллипсом.

Аналогично можно получить два других выражения гистерезиса в проекциях на оси Оу и От.

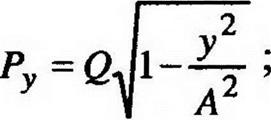(2.30)

1 72
Р’-°Г-л>	(2.31)
или в безразмерном виде
я зГл	(2.32)
У Q А2
р — Pz — ll z	(2.33)
z V

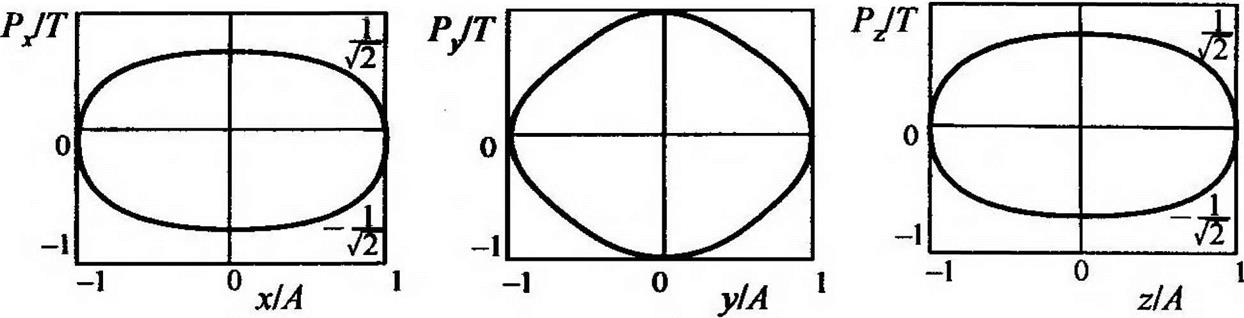
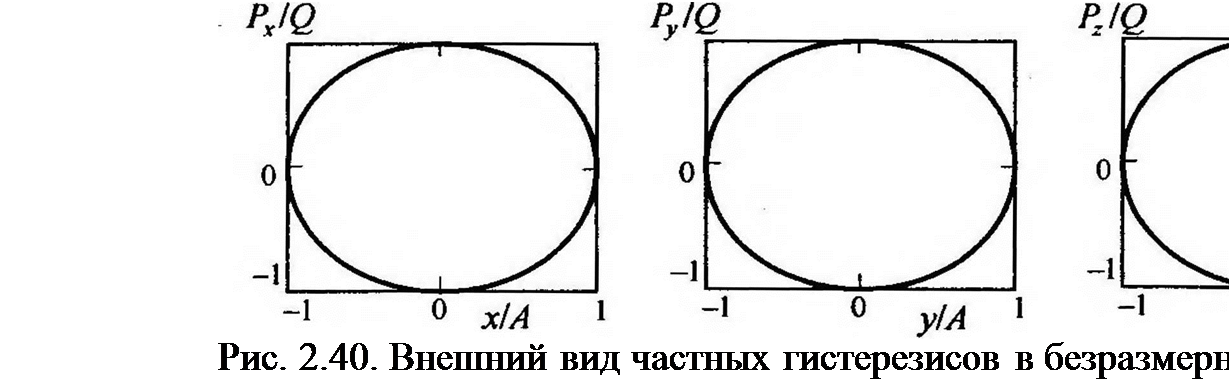
Таким образом, в рассматриваемом нами случае все частные гисте­резисы в проекциях на оси координат в безразмерном виде (2.29), (2.32), (2.33) являются эллипсами (рис. 2.40).

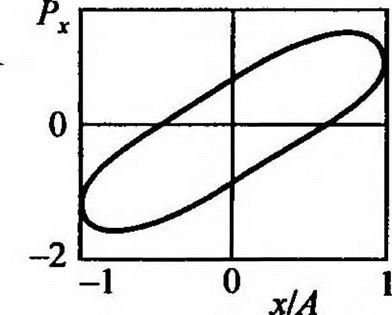
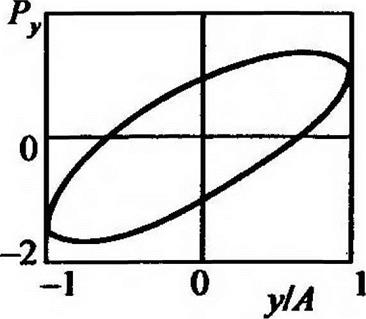
На рис. 2.41 показаны очертания гистерезисов с учетом перемен­ности скорости V от времени в координатах

fpx	V	( p > ҐУ У	и	(й. z)
U’ a	*	T * A V /	У	Т’ А)

Сравнение двух серий графиков (рис. 2.40 и 2.41), а также ре­зультатов [131], показывает, что пространственное нагружение систе-

Рис. 2.41. Внешний вид частных гистерезисов в безразмерном виде с учетом переменности вектора скорости

мы конструкционного демпфирования имеет качественное отличие от двухмерного нагружения.

Эллипсная форма гистерезисов несколько изменяется при добав­лении третьей гармонической компоненты за счет переменности за цикл нагружения модуля вектора скорости V (см. выражение (2.14). Кроме того, амплитудные значения проекций сил сопротивления дем­пфера на оси Ох и Oz меньше модуля силы Т в 1/у2 раз. Это

обстоятельство следует учитывать при переносе результатов экспери­ментальных исследований силы трения в демпферах сухого трения, определенных при одноосном нагружении, на случай пространствен­ного нагружения. Следует также отметить, что трехмерность нагру­жения приводит к изменению характера коэффициента демпфирова­ния. Этот параметр становится зависимым от скорости движения.

В заключение определим величину рассеянной за цикл энергии. Для этого воспользуемся выражением длины траектории [73J, кото­рая в нашем случае равна

L ~п |~(а + | » (2-34)

где а и Ь — полуоси эллипсиой траектории движения точки М (см. рис. 2.39). Здесь а — А; . С учетом этого длина траектории

L = 2,41 5il4, (2.35)

а рассеянная за цикл энергия, численно равная работе постоянной силы Т на пути L,

Если воспользоваться общепринятой гипотезой о том, что при совместных колебаниях можно осуществлять расчеты характеристик демпфирования, как при одноосных нагружениях, то получим вели­чину рассеянной энергии в виде

г-

Wcyx= 12АТ. (2.37)

При этом погрешность составляет значительную величину:

d = (Wcyj/W) = (12ЛГ/2,415яЛ7) = 1,58. (2.38)

Если к силе сопротивления Т добавить силы упругого сопротив­

ления, пропорциональные смещению

Рх =rcos(V, x)+fct; (2.39)

Ру =Tcos(V. y)+ty; (2.40)

Pz = Т cos(V, z)+kz, (2.41)

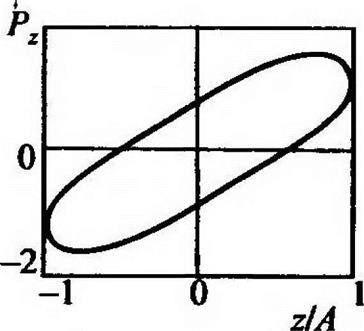
то частные гистерезисы разворачиваются на угол, пропорциональный величине k в выражениях (2.39)—(2.41) (рис. 2.42).

Многие исследователи при составлении уравнений движения меха­нических систем пользуются понятием жесткости. В общепринятом смысле жесткость — это производная от силы по перемещению в заданной точке нагрузочной характеристики упругой системы.

Для пространственных упругодемпфирующих систем с конструк­ционным демпфированием жесткость определить не так просто. Дело в том, что определение производной от векторной функции силы по перемещению предполагает возможность деления вектора силы на

Рис. 2.42. Гистерезис в пространственной виброзащитной системе при наличии восстанавливающей силы, пропорциональной смещению

(Г= 1,4-1)

вектор перемещения. Однако в математике операция деления векто­ров не определена. Для обхода этих трудностей в свое время Гамиль­тоном была разработана теория кватернионов, в которой операция деления величин типа векторов определена [137].

Обратимся к рис. 2.39. Для пространственной виброзащитной си­стемы вектор внешней силы Р не совпадает по направлению с векто­ром перемещения р, конец которого находится в точке М(х, у, z). Представим векторы Р и р в виде кватернионов с нулевыми значе­ниями действительных частей:

Выражение (2.43) можно записать в виде -C = C0-CJ-Cyj-Czk, где действительная часть кватернионной жесткости Рх* + РуУ + pzz

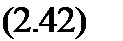
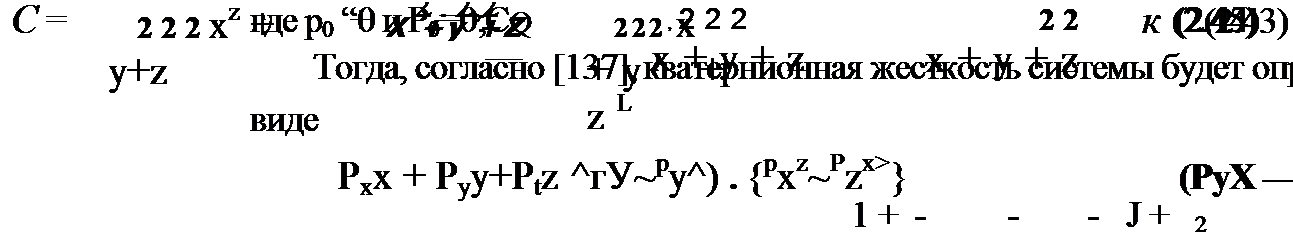
р = рQ+xi+yj+zk; P =

а компоненты мнимой (векторной) части кватернионной жесткос­

г (РУ2 ~ ИЛ. х х2+у2 + г2’ г — (PzX~Pxz) . У 2 . . 2 . _2 *

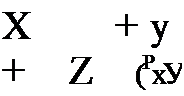
ти соответственно равны:

(2.46)

(2.47)

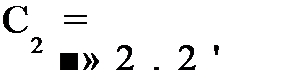(2.48)

дГ +y+z v 7

Произведение кватернионов (2.42) дает нам кватериионный мо­мент сопротивления пространственному движению объекта в систе­ме координат с ортами (/, i, j, k):

М = ~[Рхх + Руу + Pzz)+ (Pyz — Pzy)i + (Pzx — Pxz)j + {РХУ~ Pyx)k. (2.49)

Выражение (2.49) можно представить в виде:

М =M0+

М 0 = ~{рхх + руУ + pzz}> (2.51)

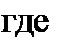Ux={pyt-Pzy (2.52)

My=(Pzx-Pzz) (2.53)

М z ={рху — Рух (2.54)

Анализируя выражения (2.43)—(2.54), можно увидеть, что ком­поненты кватернионов жесткости С и момента сопротивления слож­ному движению М состоят из действительной и мнимой частей. При этом мнимая часть момента сопротивления складывается из проек­ций момента сил сопротивления на соответствующие оси, а мнимая часть кватернионной жесткости — из аналогичных проекций жестко­сти на те же оси. Действительная часть кватериионного момента представляет собой полную энергию деформации системы, а действи­тельная часть кватернионной жесткости — частное от деления пол­ной энергии деформации системы на квадрат модуля смещения виб­ратора р. Эти параметры в течение цикла нагружения изменятся сложным образом.

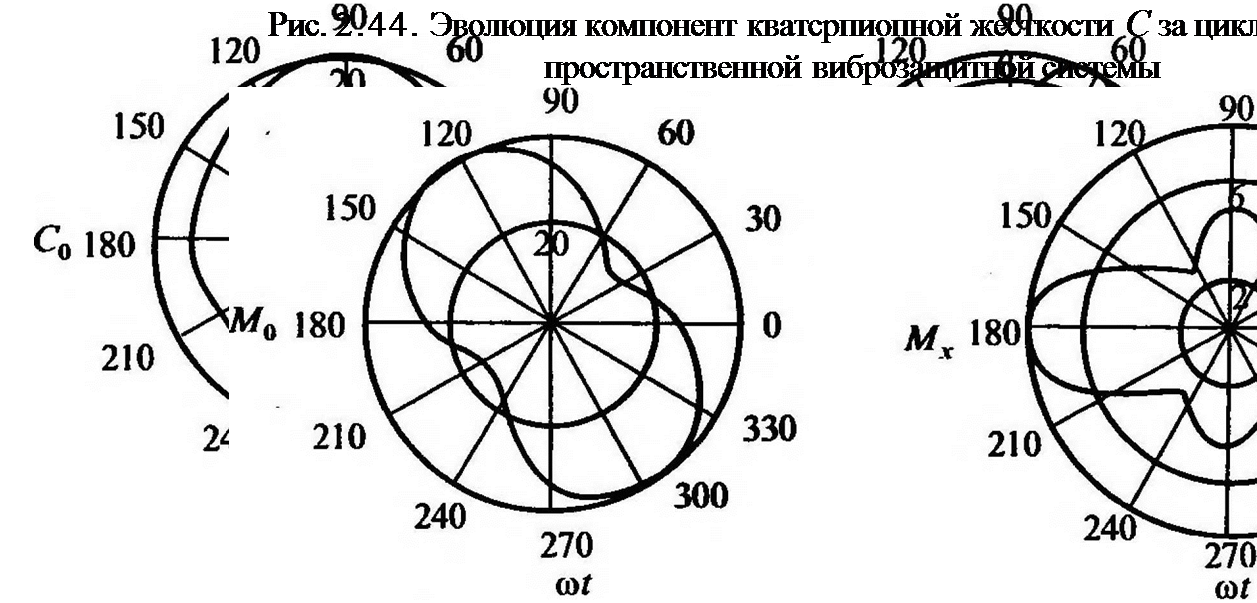
В качестве примера приведем несколько графиков изменения вве­денных параметров. На рис. 2.43 показано изменение векторных частей кватернионной жесткости C((ot) и кватериионного момента

M((Qt) в пространственных координатах; на рис. 2.44 — эволюция векторных компонент Cx((nt), Су(аЛ) и Cz((dt), на рис. 2.45 — эволю­ция векторных компонент Mx((Ot), М ((at) и Mz(<at).

Представленные на рис. 2.43—2.45 графики изменения кватернион- ных компонент жесткости и момента сопротивления движению рас­считаны для абстрактной виброзащип юй системы. В каждом конкретном случае для расчета кватернион ных параметров необходимо знать ис­тинные зависимости силы трения в унругодемпфирующей системе и восстанавливающей силы от ее геометрических и физических пара­метров. Такими параметрами для многослойных гофрироваїшьіх паке-

тов являются: число лент и воли гофров в каждом пакете, толщина и ширина ленты, высота гофров и предварительный натяг в радиальных пакетах (см. рис. 2.36, б), внутренний и наружный радиусы шайб, их число, толщина каждой шайбы, число волн по окружности шайб, высо­та гофров и натяг для осевых демпфирующих пакетов (см. рис. 2.36, в), шероховатость поверхности лент и шайб (коэффициент трения), мо­дуль упругости материала демпфирующих пакетов, диаметр корпуса турбомашимы, в которую устанавливаются пакеты.

Для пространственной виброзащитной системы, показанной на рис. 2.37, такими параметрами являются — конструкция тросовых элементов, число проволок в сечении, их диаметры, средний радиус изгиба криволинейных участков, число и расположение элементов в ансамбле, состояние поверхности проволочек и др. По этим пара­метрам можно создать математические модели расчета зависимос­тей сил неуиругого сопротивления и восстанавливающих сил систе­мы [111], которые затем можно использовать в предложенной методике для расчета кватерииоииых параметров. Можно восполь­зоваться также и экспериментальными данными, полученными на базе испытаний конкретной системы виброзащиты в направлениях осей Од:, Оуи Oz. Обработку этих данных можно выполнить по методикам, изложенным в работах [131, 111].