КОМПЛЕКСА АВИАЦИОННЫХ СИСТЕМ
4.1. ОБЩАЯ СХЕМА УПРАВЛЕНИЯ
ДЛЯ НЕПРЕРЫВНОГО СЛУЧАЯ 4
Пусть состоящее комплекса АС характеризуется вектором X(t) = {x(t), x2(t), xN(t)}, составляющие которого суть дис
кретно контролируемые параметры. Общее число контролируемых параметров комплекса равно N.
Требование дискретного контроля является естественным для всех реальных технических систем. Поэтому считаем, что вектор
X(t) наблюдается с постоянным интервалом At в моменты /ь t2……………….
Считаем также, что распределение вектора X (t) нам известно, т. е. известно
F(z)=P{X(t)<Z}=P{x1{f)<zl,…,xN{f)<zN}. (4. 1)
Предположим, что область L допустимых изменений вектора X(t) или пределы изменения его составляющих заданы. Обозначим их как L(Bl)—для верхней границы составляющей х,• и L^ — для ее нижней границы (£=!,…, N), тогда HN)y
где /.(‘)== [/.Л /Г], / = 1, N. Полагаем, что выход любой составляющей вектора X(t) за допустимые границы (отказ комплекса) приводит в среднем к потерям С+А’, где С — средние потери, связанные с упреждением или ликвидацией отказа (например, время замены или регулировки отказавшего или находящегося на грани отказа блока или системы) и А’ — некоторый штраф вследствие отказа комплекса.
Обозначим через tq момент первого выхода любой из составляющих вектора X(t) за допустимые границы и введем следующую функцию потерь:
![]() — • n<q tn
— • n<q tn
(С + Л’)
При наблюдении за вектором X(t) следует выбрать такой момент 4, определяющий оптимальное правило остановки наблюдений— упреждения отказа комплекса (назовем его оптимальным моментом остановки наблюдений), при котором
M[yts] = minM[ytn],
г i> min берется по всем правилам остановки наблюдений из неко — riipwo заданного класса.
После такого момента 4 эксплуатация комплекса строится таким образом: если до момента 4 хотя бы один параметр комплекса мы и нм за допуск (в момент tg), то сразу же после отказа восста — п. шли ают отказавший блок или систему и проверяют (при необхо — м и мости регулируют) все остальные параметры комплекса (затра — II,! и этом случае равны С+Л’). Если до момента 4 параметры не выходили за допустимые пределы, то все проверки и необходимые |н-| > лировки осуществляются в момент 4 со средними затратами С.
І Ірсдполагаем далее, что наблюдения за вектором X(t) не влекут пі собой никаких затрат.
Определим момент оптимальной остановки наблюдений 4- Оче — иидпо, что при п— <q, если момент 4i есть некоторый (не оптимальный) момент остановки наблюдений,
М ytjx (4),…, 26 (4-!)] = -£- р {■*! (4) (4)є=
IX (4) ЄІ,…, X (4-і) е4} +
І ^ [ 1 — Р Іхг (tn)EELW,..„ xN (4) ЄЕ4" | 26 (4) ЄД…, * (4-х) ЄЇ}].
(4.2)
![]()
Для краткости записи условную вероятность в формуле (4.4) сокращенно обозначим как Р{ }. Тогда, учитывая, что tn = nAt,
А’ (/і-l)
Пусть s будет таким наименьшим п, при котором
(4‘3>
А’ (и—1)
Тогда для всех /;>s 1—Р{ }>С/А'(п—1), так как левая часть (4.3) увеличивается (для любой стареющей или постепенно разрегулирующейся технической системы), а правая уменьшается с ростом п. Согласно теореме 4.1, доказательство которой приводится в следующем параграфе, момент остановки наблюдений ta является оптимальным.
Пусть A/,* = min(fs_i, ^|«]-і). где [g] — наибольшее целое, меньше д. Тогда оптимальная стратегия эксплуатации комплекса заключается в том, чтобы проверять его (при необходимости восстанавливать или регулировать) через время N*. ‘
Рассмотрим несколько частных случаев. Если предположить, что между соседними наблюдениями вектора X(t) .возможен выход за пределы допусков не более одной его составляющей, то (4.3) можно записать в виде
шах [1 — Р(хг (tn) е LW/X (А) Є £,…, ЛГ (/„„О Є
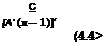 -P{xN {tn) ЄЕ Lm/X (/0 Є L,..„ X (/„.О ЄЕ L} >
-P{xN {tn) ЄЕ Lm/X (/0 Є L,..„ X (/„.О ЄЕ L} >
Если составляющие вектора X(t) являются гладкими (производная реализации не меняет знак в пределах шага контроля), то
(4.4) запишется так:
max[(l — P{x1(tn)<min(L{K1)—x1 (<„_!), №—x1(tn_1)X(tj є
ЄІ….Д I P {xN (/„) < min (LiN) — xK (tл_і),
^N) < xN (in^))/X (/,) ЄЕ L,…,X (*„_,) ЄЕ L} > C.
A (n— 1)
Для независимых составляющих вектора X(t), например, для случая (4.8)
И, наконец, при независимых составляющйх (параметрах) комплекса и независимых их изменениях по шагам контроля
max [1 — P{Xl (*„) ЄЕ № I jd (*„_,) Є К1)};…;
1 -P{*N ft,) ЄЕ iW | *„(/„. _,)є №}] > —
[4′ (и — 1)]
В случае дискретной функции распределения (4.1) для управления по описанному выше алгоритму (например, при контроле по принципу «да — нет» — наблюдении за числом отказов комплекса систем) необходимо знать состояние каждой наблюдаемой системы
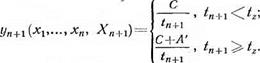
![КОМПЛЕКСА АВИАЦИОННЫХ СИСТЕМ Подпись: ‘Р влипшем выражение для средних удельных потерь: (С;К4'} [1 - р {Хп+1 < L - А (/„) I х2)..., хп}] =](/img/1308/image151_1.png) |
|
и гг наработку к моменту наблюдения. При этом на структуру комплекса никаких ограничений не накладывается. Известную труд — ІМІГП. здесь представляет определение области отказовых состоя — мімі комплекса.
І Іусть обобщенный параметр, характеризующий состояние комплекса при эксплуатации, есть случайно меняющийся скалярный параметр X(t), который отражает процесс накопления нарушений. І’ачтмотрим монотонно возрастающий случайный процесс X(t) с приращениями Хп, п— 1, 2,… в моменты контроля. Таким обранім наблюдаем некоторую последовательность зависимых случайных величин Хи Х2, …, Хп, . .. Пусть функция :<р(Хь Х2, .., Хп, …), принимающая значения 0, 1, 2, …, характеризует правило остановки (наблюдений). Будем считать, что если xp(XIt Х2, …, Хп, …
) т, т. е. Xi=xu Х2~ х2, Хт—хт, то процесс наблюдения
икн впивается на m-м шаге. Если іф(Х|, Х2, …, Хп, …) =0, то это означает, что принято решение вообще не производить наблюде — ІИІи над случайными величинами.
Отмстим, что записи Х, х2, …, х„_і относятся к уже наблюденным приращениям (реализациям случайных величин Х1г Х2,…,
. . ., А, а если мы не наблюдали приращение, то считаем его случайным и обозначаем символом X. Например, если последнее наблюдение закончилось в момент £„_ь то приращение процесса V (/) от t„-1 до tn обозначаем через Хп.
Введем функцию потерь для отыскиваемого правила остановки наблюдений:
(4.5)
Функцию (4.5) поясним следующим образом: наблюдая процесс Х(1) до момента /„ включительно, решаем, какие будут удельные потери, если остановить процесс в момент tn, здесь С — среднее время возвращения процесса в ноль, если X(tn+i)<L, а | /Г — среднее время его возвращения в ноль при — Х(їи+і)>£, іде /. допускаемая граница изменения процесса X(t), iz—момент выхода процесса X(t) за уровень L. Так как числитель дроби в правой части (4.5) случаен, то необходимо найти оптимальное правило ф*, минимизирующее средние удельные затраты, т. е.
min Ж yn+i (х1,…,хп, Хп+1).
Покажем, чтобы потом воспользоваться известным результатом, что
^ Уп+1 Хп, ^n+x)]t/n (-ХГц…,ЛГЛ_1, Xп),
если процесс наблюдения остановить не позже момента ф*, т. е. при1
….. Хп) (4.7)
и если
1 — P{Xn+1<L-X(tn)/xlf х2,…,хп}<^~. (4.8>
71
Подставляя (4.8) в (4.6), убеждаемся, что наше утверждение верно. И наоборот, А1 [yn+1(xv…, хп, X’n+l)> y„(xv…, хп_и Хп), если. процесс наблюдения остановить не раньше момента ф*, т. е. при
«><?*(хъ…,хп) (4.9>
и если
1 — P{Xn+1<L — X (tn)/xi, х2,…,хп}^>С/Л’п).
Подставляя последнее выражение в (4.6), убеждаемся, что и обратное утверждение справедливо.
Пусть п* есть такое п, при котором имеем знак равенства в (4.7) и (4.9). Тогда
<р:*:(х1,…,хп, Хп+1)=п*. (4. 10)
Так как выполняются условия теоремы 4.1, то утверждение (4.10) верно и п* нужно отыскивать как наибольшее п, при котором еще — верно выражение (4.8). Найдем из (4.8) уравнение кривой оптимального упреждающего допуска в предположении, что приращения Хп независимы и одинаково распределены: F(L—Xr(tn)^l— —С/An. Взяв от обеих частей этого неравенства функцию обратную F, получаем
или X (tn) < і — F~x ^ 1——- •
Управление с использованием кривой оптимального управления оказывается весьма эффективным. Для случая независимых, одинаково распределенных приращений процесса X(t) подробные количественные данные, характеризующие эффективность эксплуатации технических систем по состоянию (оптимального управления монотонным процессом), приведены в работе [1].
4.2. ДОКАЗАТЕЛЬСТВО ОПТИМАЛЬНОСТИ УПРАВЛЕНИЯ ДЛЯ ВЕКТОРНОГО СЛУЧАЙНОГО ПРОЦЕССА
Пусть (U7, Fn, Нп)—векторное вероятностное пространство для каждого л=!1, 12, … с точками океВ-‘, где К — размерность. некоторого наблюдаемого в моменты tu <2… вектора Хп (и=1, 2,…), т. е. имеем дело с последователь-
и,„ іі.’о векторных зависимых случайных величин Xi(ti), Х2(12),..Xn(tn), где /.. (п — случайные моменты времени, с заданным совместным распреде
лением //(X,(tt), X2(t2),…, xn(tn), U, fc,…, tn. Причем состояние процесса „ іаиисит от всех прошлых значений Х, Х2,..Х„_, и от распределения мі імен га t п.
І Іоследовательность (уп, Fn) является некоторой стохастической последо — н. тП’.’іііііостьіо: Уп—последовательность случайных величин, Fn — последова — ,!• 1ЫЮ1 ть векторных о-алгебр (о= (ои ог, ■ ■ ., Ок)) с F„eFB+ieF и у„ измерима относительно Fn, уп является некоторым функционалом, определенным: їм траекториях процесса Хп, ЩУп] существует и — оо оо.
Ііудем в дальнейшем интересоваться выбором некоторой случайной (поло — ,1,11 ІеЛІ. ІЮІІ и целой) величины s = s(coK), которую назовем моментом остановки наолюдений за процессом Хп, {s^/i}^Fn и {з<оо}=Ц7. Здесь (и в дальнейшем) с помощью фигурных скобок {…} обозначено множество всех «к, упшлстноряющих соотношению внутри скобок. Задача будет состоять в отыс — I,.піни такого значения величины s.(если оно будет существовать), которое минимизирует М[уп]. Определим момент остановки наблюдений следующим пора him [75].
I’.а усмотрим наряду с последовательностью B, eFn последовательность
О = В0<=…Вп+1<=…; б Bn = W, (4. 11>
момент остановки s, определяемый как {s<;m}=B„, тогда, очевидно, {s = «}= /(„ Вп_1.
Если последовательность («/„, Fn) является такой, что В„—{М[уп i — //„} удовлетворяет (4.И), то назовем этот случай монотонным и определим момент остановки s как
{s <л} = {М [Уп+і/Хп] < Уп}, (4. 12>
і не .s удовлетворяет записи
![]()
![]() M[yn+iFn[ >/П’ I <Уп
M[yn+iFn[ >/П’ I <Уп
Мездс в приложениях для рассматриваемого монотонного случая будем в іііюііііться определением момента остановки s, для которого верно (4.12), и следующем виде: s равно наименьшему положительному целому /’, такому,
Ч III
м [і/(+і|В/] < У І. (4. 14>
Однако даже и в немонотонном случае всегда можно определить случай — нні величину s с помощью правила (4.14), полагая s= оо, если не найдется і. нм и о j=s, при котором верно (4.14). Необходимым и достаточным условием і мнеетиопания момента остановки s, для которого справедливо (4.13), является монотонность процесса Хп и выполнение для s условия (4.14).
Покажем, что в монотонном случае можно выбрать такой момент оста — .ч (при справедливости (4.14), при котором достигает минимума величин, і Л4[і/Л — Отметим сначала, что рассматриваемые ниже моменты остановки •• н I янляюгея такими, для которых существует Л4[гд] и Myt.
Теорема 4.1. Если для каждого п
м [Ы^п] < уп, S > п, (4. 15>
" XI [ytFn] > уп, s=n, t>n, (4.16)
ю M[«/s] <Af [yt]. (4.17)
Лемма 4.1. Если M[//s] ограничено и выполнено условие (4.17) для ‘• аждого t, то (4.15) и (4.16) справедливы также для каждого t.
Доказательство теоремы 4,1. ‘Учитывая, что М[у по-разному определяется в зависимости от соотношения s и п и используя формулу полной Вероятности, получим
\т
M[ys] = І] UsdH (Xі (/,), Х2 (h), …Xs (tsy,
![]() n = 1 {S-/2, /<nj
n = 1 {S-/2, /<nj
oo
■i, h…. ,^ + 2 J j — — ■ J УпйН № (h), X2(t2)………………….. Xn(tny, tlf t2,…,tn) =
/2=1 2/г раз
{$=/2, t >/2 J
CO
” JJ • • • J UsdH (Aj (^i), X2 (^2) * • • • > Xn (tnY> ^11 ^2» ■ • • »^«) H-
/2 = 1 2/2 раз
{S>/2, />/2}
00
■+ 53" Я ■ ■ ■ I yndH(Xi№)• ■ ■ • — xnVn); h, t2,…, tn). (4. їв)
/2 = 1 2a раз
[5=/2, />/гJ
На основании (4.15), (4. 16) и (4.18)
со
~M [у5] < У] (‘•-■J yndH (Л’і(П). X2(t2),…, Xn(tn); tlt t2,… ,tn) +
4=1 ‘2/г раз
JSV/2, f=/2}
00
+ 2 J ■ ■ • J № (*i>. *2 (/2),. -., xt (/,); tu t2……………………………. t() = M [yt],
n=l 2/ раз
{S = tl. <>«}
Следовательно, мы доказали, что в монотонном случае при выполнении условий (4.15) и (4.16) момент остановки наблюдений s является оптимальным — доставляющим минимум величине М[у3. Это и означает, что теорема 4.1 доказана.
Доказательство леммы 4.1. Для фиксированного п
V = {s > п и М [ys|F„] > уп} є Fn.
n { s, «5Е V;
-Определим t = 1
( п, а» є ІЛ
Тогда F является моментом остановки. Так как M[ys] ограничено, то согласно (4.17) Л1[у„]<оо и, значит, М[у t,] существует.
Покажем, что М [yt,] = М [ys]:
М [yt,] = J… J ut, dH (*, (/,), *2 №)……………….. Xt, {ttX tu t2. +
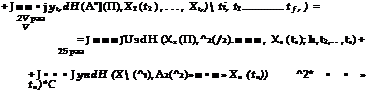 2n раз V
2n раз V
< J • ■ • J ysdH (X (ti), X% (^2)» • ■ • * Xs tj t<ii • •. > ts)
2s раз {<‘-*}
+ J • • • І У^Н (Xi ((j), X2(t2)……….. Xs(ts); tlf t2,…, /s)=Al[f/i].
2s раз
V
Юднако M [yt,] > M [уД.
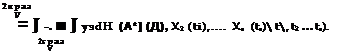 |
оіпода следует; что P(V) = 0, что и доказывает справедливость (4.15).
Для доказательства (4.16) положим V={s = n, t>n и M[tjtlFп]>уп} и определим
I (и да можно по аналогии с предыдущим показать, что и в этом случае
АЦиг<м ys].
Оісдовательно, Р(V) = 0, что и доказывает справедливость (4.16).
4:1. СХЕМА УПРАВЛЕНИЯ ДЛЯ ДИСКРЕТНОГО СЛУЧАЯ
Рассмотрим оптимальный алгоритм эксплуатации комплекса Ас, обладающего избыточностью по надежности (эффективности.) Принятие решения о дальнейшей эксплуатации комплекса систем шлжпо основываться на информации о состоянии систем, отображаемой по принципу «да» — «нет» (работает или не работает в дискретный момент контроля та или иная система). Предполагается, что комплекс обладает избыточностью по эффективности (надежности), т. е. отказ ряда систем в комплексе не является отказом комплекса в целом. Оптимизацию решения проводят по критерию, минимума средних удельных затрат на эксплуатацию комплекса, складывающихся из затрат (времени, стоимости) на устранение — нарушений (отказов систем и затрат, связанных с отказами комплекса). При этом эффективность комплекса не должна быть ниже — некоторого приемлемого уровня. Таким образом, задача отыскания — оптимального алгоритма эксплуатации АС с избыточностью относится к классу многокритериальных задач. Составным критерием в мой задаче является критерий «готовность (стоимость) —эффек — I явность».
Оптимальный алгоритм эксплуатации комплекса систем по бинарной информации о работоспособности систем сводится к проверке следующего стохастического неравенства:
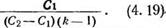 /'(v^), tk ] Є A, I [v {ti), th i=0, &—!]}<
/'(v^), tk ] Є A, I [v {ti), th i=0, &—!]}<
В левой части неравенства — условия вероятность отказа комплекса за время Дt—th — tk-1 при условии, что состояния систем в момент th і известны и таковы, что комплекс в целом не находится п состоянии отказа. Вектор v(4) = {vi(A), t, …, vjv(0> ^v} харак — іч рпзуст с учетом наработки состояние каждой из N систем, по принципу «работает — не работает», т. е. для каждой системы
0, если l система работоспособна в момент t;
1, если она в момент t находится в состоянии отказа, i=,…,N.
Область Л0 обозначает набор таких состояний систем, которые характеризуют отказ комплекса (эффективность комплекса равна нулю).
В правой части неравенства (4.19) Ci/(C2 — СД—некоторая константа, характеризующая (в среднем) отношение затрат на возвращение комплекса в исходное состояние в момент предупредительного восстановления (к этому моменту комплекс не отказал) Сі к разности между затратами на его восстановление после отказа (в ряде случаев сюда входят и затраты, обусловленные отказом комплекса) С2 и затратами на предупредительное восстановление/ неотказавшего комплекса С.
Отсчет времени ведется дискретно: th=kAt, где At—шаі контроля комплекса, k — номер шага контроля.
Основная трудность при «работе» с оптимальным решающим правилом (4.19) заключается в определении условной вероятности. Для каждого комплекса это самостоятельная и порой довольно сложная задача. Для ее решения необходимо составить схему соединения элементов каждой системы комплекса и комплекса в целом по надежности (эффективности) и рассчитать вероятность отказа комплекса. Если схема соединения элементов по надежности не является параллельно-последовательной, то расчеты существенно усложняются.
Область Л0 отказов комплекса составляется по схеме соединения элементов (систем) по надежности с учетом влияния отказа каждого элемента на эффективность работы системы.
Работу алгоритма (4.19) поясним на конкретном примере. Предварительно заметим, что процесс накопления отказов, или нарушений, в системе с избыточностью является ступенчатой и возрастающей во времени функцией. Если эту функцию сгладить плавной кривой, то получим процесс, исследованный в § 4.1. Именно монотонность накопления нарушений лежит їв основе обоснования оптимальности алгоритма (4.19).
Рассмотрим сложный авиационный комплекс с избыточностью по надежности, которая меняется в зависимости от выполняемых комплексом задач. ІІзлагаемьіе рассуждения относятся к авиаци-‘ ■онному комплексу в целом, так как ему присуще выполнение разданных задач, а следовательно, используются и различные системы комплекса.
Пусть комплекс состоит из N элементов (блоков, систем и т. д.), а 0г(О есть наработка i-ro элемента комплекса к моменту t. Тогда в произвольный момент t состояние комплекса может быть описано вектором v (/) = {vj (/) 0, (/’);…; vw(/), Од,(/)}.
Обозначим через А множество всех состояний элементов, образованных по принципу «да — нет» для каждого элемента (например, все элементы исправны, неисправен один элемент и т. д.). Очевидно, что множество А содержит некоторое подмножество Л о. Если в него попадает вектор v(t), комплекс не может выполнить стоящую перед ним задачу с заданной эффективностью. Для каждой выполняемой комплексом задачи должна быть составлена
схема соединения его систем по надежности. Чаще всего используется параллельно-последовательная схема. Для каждой задачи должен быть задан свой уровень эффективности. Это означает, что £/.-я задача характеризуется своим значением подобласти q= = 1,…, п, где п — число решаемых комплексом задач.
Покажем, как при решении комплексом ряда последовательных задач должна осуществляться его оптимальная эксплуатация с использованием алгоритма (4.19).
Предположим, что число задач равно п, причем при решении q-fi задачи используется Ng его систем, <7=1,2, …, п, Ng^.N. Допускается, что при решении <7′-й и 1-й задач может быть использована часть одних и тех же систем. Все системы с начала функционирования комплекса включаются в работу. Комплекс функционирует непрерывно до начала предупредительного. восстановления или до такого момента времени, в который он не может решать хотя бы одну из п поставленных задач. Последовательность решения задач во времени при этом нас не интересует. Допустим, что /10(9) (<7=1, ■■■, п) — подобласть состояний комплекса, при попадании в которую вектора v(t) = {vj(l), 01 (t); …; Vjvg(O0M<?(O} комплекс не может с заданной эффективностью выполнить q-ю задачу.
Тогда для q-й задачи алгоритм, аналогичный (4.19), запишется так:
Пусть № и tz — соответствующие моменты первого невыполнения (4.20) и первого наблюдения события [‘vq{t), /] Є Ло?) с точностью до шага контроля. Тогда момент вывода комплекса на техническое обслуживание (предупредительное восстановление или ремонт) определяется как (общий отсчет времени ведется с начала работы системы, т. е. с to=0):
min (d! 4°,.., №, 4n)).
Таким образом, комплекс не может быть использован по назначению, если он не в состоянии выполнять любую из поставленных перед ним задач. Возможно здесь и другое предположение: комплекс не может быть использован по назначению, если он не в состоянии выполнить задачу, стоящую перед ним в фиксированный момент времени. В этом случае с момента начала работы комплекса нужно для каждой задачи вести вычисления по алгоритму (4.20). В бортовой вычислитель, помимо алгоритма времени, должна вводиться и информация о фактическом состоянии систем, участвующих в выполнении каждой задачи. В вычислителе по-прежнему содержится информация о возможности выполнения комплексом любой задачи с момента последнего контроля его состояния. Если к моменту 4** для <7-й задачи не выполняется (4.20), то техническое обслуживание комплекса осуществляется в момент tiV’.
