Основные понятия статистических гипотез | Авиация - коммерческая, гражданская, спецавиация...

Статистическая гипотеза — это утверждение относительно одного или более параметров распределения случайных величин или о самой форме распределения. Процедура проверки гипотез — правило, которое позволяет для любого множества наблюдений Z>—>Zn получить

решение: принять или отклонить проверяемую гипотезу Н0 (нулевую гипотезу).

Полезно представить множество выборочных значений Z,—,zn в

виде точки л-мерного пространства. Тогда точки, для которых гипотеза Я0 отклоняется, относятся к критической области со.

Ошибки, допускаемые при проверке гипотез, разделяют на два типа:

• ошибка первого рода — отклонение гипотезы Н0, когда она верна;

• ошибка второго рода — принятие гипотезы Н0, когда верна какая-либо другая (альтернативная) гипотеза Hv

Вероятности ошибок первого и второго родов характеризует достоверность статистического решения. Вероятность ошибки первого

рода равна P{z,—,zn принадлежит со|#0} = а. Величина а называется уровнем значимости, или размером критической области. Вероятность ошибки второго рода равна 1- P{z,—,zn принадлежит

(о|Я,} = р и зависит от гипотезы Я,. Вероятность р называют оперативной характеристикой по отношению к Я,, а величину 1 — Р — мощностью критерия.

Примеры определения точности оценок одномерных стационарных детерминированных параметров

Таблица 10.3

Закон распределения	Оценка	Дисперсия	Доверительный интервал
1	2	3	4
Нормальный закон распределения:
2 а — известно	1=1	— а2 Л [Щ= — п	А [ Мк = М — «i.^a/Vn, ‘ А М =M+«i_a/2 a/Vn, V где ttj _ а/2— квантиль нормального распределения
2 а — неизвестно #	п р2 1 >г-ч. ■ Л ■уо=л_1 2 й/ ^ / = 1 /= 1	д[^2] = 2а (”-1) п	ми-м tx_а/2( = 1 — а/2 ^ V где /1а/2 — квантиль [ 2 ■Уо(И-І) аН’х?.^(и-1)’ 2 ав — 2 . , > Ха/2 (л ~ 1) V гае Х[ .„/2 > Х^2 — квант	и -1) 50/а/л, п -1) J0/V«, /-распределения _ 2 £2Л аи 2 » Хі-а/2^ _ 2 а в 2 ’ 1 *а/2 ^ 2 їли % — распределения

Закон распределения Рэлея

/=1

* в2 DW = —

г _А

_ 20л

ен — 2

хї-з^оя)

„ 2вл

®н — 2

%о/2 <2/I>

Биноминальный

закон

распределения

D [Д] = * (1я~ *

где В

^ Л (л — /)! ^ "1 _г2’

г= 0

г= 0 ‘

где + у2-1 =Y

RVL=Bl {d, n-d+)

Д. = В (d+l, n-d)

£/i=i _ [2d; 2(я — £/+1)]

(n-d+) + dF. 2d,2{n-d+)’

1 ‘2

(d+)F.’ [2(rf+l), 2(л — d)] t»“(n-rfH-(d+l)/V1 [2(d +1), 2(л — d)] ’

. . 2? — квантили В-распределения;

1 Т2 “l

F — квантили F-pacпределения

-Т2 Yj

Гипотезы бывают простыми и сложными. Гипотеза называется простой, если она точно определяет распределение случайной величины, в противном случае она называется сложной.

Для принятия решений относительно проверяемых статистических гипотез используют критерий значимости. Последний основываются на принципах практической достоверности и практической невозможности.

Событие, которое при заданном комплексе факторов обязательно произойдет, называется абсолютно достоверным событием. Абсолютную достоверность можно установить лишь теоретически, путем логических умозаключений. Сюда относятся в основном математические истины и некоторые выводы точных наук. Большинство практически достоверных событий не являются абсолютно достоверными, однако вероятность их осуществления достаточно высока.

Из принципа практической достоверности вытекает принцип практической невозможности: события с очень малыми вероятностями можно в практических приложениях считать невозможными. Практическая невозможность осуществившегося события отвергает случайность его появления и заставляет пересмотреть исходные предпосылки при вычислении вероятности его появления, т. е. пересмотреть исходную гипотезу.

Использование принципа практической невозможности для доказательства неслучайного появления события с малой вероятностью называется принципом значимости. Проверка статистических гипотез в соответствии с принципом значимости осуществляется следующим образом. Выбирается уровень значимости а и соответствующая ему

вероятность 1 — а. По этой вероятности, используя нулевую гипотезу о распределении случайной величины у, представляющую собой

функцию выборочных значений Z,…,zn, находят квантили Уф и У-а/2, такие, что Р{у < Уф}- а/2; Р{у < ух. ф] = 1 — а/2. Значения Уф, Уі-а/2 называются критическими, а неравенства У < Уф и

У > У-ф образуют критическую область проверяемой гипотезы. Если измеренное значение у0 попадает в критическую область, нулевая гипотеза отвергается; если же выполняется неравенство

Уф * УЬ * Уі-а/2, (10-3)

то такой разброс в рамках нулевой гипотезы может быть объяснен эффектом случайности и нет оснований отвергать проверяемую гипотезу. Заметим, что первое решение (гипотеза неверна) гораздо более категорично, чем второе (гипотеза не отвергается). Поэтому в прак
тических задачах, решаемых методами теории проверки статистических гипотез, большое значение имеет правильный выбор нулевой гипотезы.

Полученный критерий (10.3) является двусторонним. Если одно из неравенств У < Уф или У > У-ф заведомо невозможно, применяют односторонний критерий, например у0 < ух_а.

Требования к уменьшению ошибок первого и второго родов противоречивы: уменьшение уровня значимости сопровождается снижением мощности. Чтобы разрешить это противоречие, задают уровень значимости и максимизируют мощность критерия по отношению к альтернативной гипотезе.

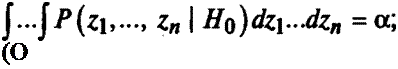Аналитически поставленную задачу можно сформулировать следующим образом: требуется так выбрать критическую область, чтобы

…p(zi, -,zn I Hi)dzi — dz„ = max.

• * (О

Решение этой задачи получают с помощью леммы Неймана-Пирсона, согласно которой искомая критическая область определяется из отношения правдоподобия:

Zn І Яр) ^ ^

где к выбирается из условия обеспечения заданного значения а. Получаемый критерий называют критерием отношения правдоподобия.

Related Post

Похожие записи: