КРИТИЧЕСКИЕ УГЛОВЫЕ СКОРОСТИ КРЕНА

При вращении самолета с постоянной величиной угло­вой скорости крена (со* — Q) условие устойчивости А0 > 0 в раз­вернутом виде записывается следующим образом:

BQi

(6.1)

>0.

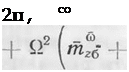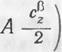
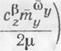
Как это следует из выражения (6.1), основным фактором, определяющим устойчивость движения, является соотношение между запасами статической устойчивости самолета по углу

скольжения щ и углу атаки thz6 и величинами, пропорциональ­ными квадрату угловой скорости вращения самолета относительно продольной оси. В связи с этим, определим вид границ областей устойчивости движения самолета в зависимости от величины Q

на плоскости с координатами th%, thy. Как это следует из условия (6.1) границей области устойчивости в таких координатах яв­ляется гипербола, описываемая соотношением

XY = — К, (6.2)

где

X = xt — AiiQ2, х, = (-Ій5$ — ^);

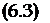
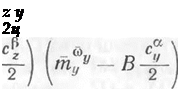Y = Yi — l-mg +

К = KoQ2, Ко = ( 4- 4

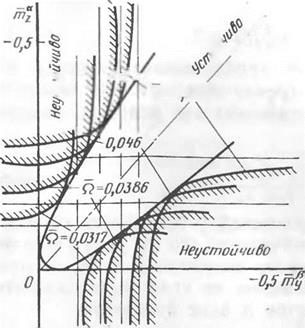
Примеры границ областей устойчивости для различных вели­чин угловой скорости крена приведены на рис. 6.1. Из выраже-

ний (6.2) и (6.3) следует, что гиперболы в координатных осях (т%, 0, /л!;) имеют асимптоты, описываемые уравнениями

—т% = ЛрО2 + ~ A^Q2; (6.4)

—thfi ■■= B[iQ2—- ~ (6.5)

В тех областях, где значения mz6 и ту существенно отличаются друг от друга, гиперболы приближаются к своим асимптотам (см. рис. 6.1). Отсюда, в частности, следует, что в этих областях значений параметров статической устойчивости самолета можно пользоваться приближенными критериями устойчивости, заменяя уравнение гиперболы уравнениями ее асимптот. На основании этих же соображений можно получить приближенные выражения для угловых скоростей крена, называемых критическими, при которых происходит потеря устойчивости рассматриваемого дви­жения самолета. Используя уравнения асимптот (6.4) и (6.5), получим

Формулами (6.6) и (6.7) целесообразно пользоваться при про­ведении предварительного анализа устойчивости в тех весьма распространенных случаях, когда запасы продольной и боковой устойчивости самолета существенно отличаются, а демпфирование движения не слишком велико. Подробный анализ геометрических

свойств границ областей устойчивости на плоскости (га°’б, ту) содержится в работе [11].

Рассмотрим упрощенную физическую картину движения само­лета при соА = со = const [11]. При вращении самолета относи­тельно оси, не совпадающей с главной осью инерции и составля­ющей некоторый угол с вектором скорости 1/, на него будет дей­ствовать, кроме аэродинамического момента устойчивости, инер­ционный момент от центробежных сил, который легко можно приближенно оценить, если предположить, что вся масса самолета распределена вдоль осей ОХ и OZ (рис. 6.2). Производя суммиро­вание (интегрируя) по всей массе самолета, распределенной вдоль осей ОХ и 0Z, получим выражение для полного инерцион­ного момента

Рис. 6.1. Пример границ областей устойчивости движения самолета при установившемся вращении по

^ > ‘ll} Jr

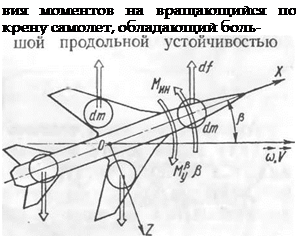§ ч Q=oos Рис. 6.2. Упрощенная схема дейст­

Аналогичное соотношение можно получить, если рассматривать отклонение самолета по углу атаки а и определять инерционный момент, действующий относительно оси 0Z

Мг ин

Оба момента, вычисленные таким образом, пропорциональны углам отклонения ф или а) и стремятся их увеличить.

Рассмотрим движение самолета по углу скольжения, пред­полагая, что степень его устойчивости по углу атаки настолько велика, что угол атаки во время движения можно считать неизмен­ным. При вращении самолета с постоянной угловой скоростью крена со = const на него кроме аэродинамического стабилизиру­ющего момента действует дополнительный дестабилизирующий момент, выражение для которого было получено ранее, пропор­циональный квадрату угловой скорости крена, который умень­шает «эффективную» степень статической устойчивости самолета. Очевидно, что потеря устойчивости произойдет тогда, когда инерционный момент окажется больше^стабилизирующего аэро­динамического момента. Следовательно, существует некоторое критическое значение угловой скорости крена, которое можно определить из условия, что самолет по углу скольжения (при анализе продольного движения по углу атаки) является ней­трально устойчивым, т. е.

(Му ИН Му а0р) О,

Условие нейтральной устойчивости может быть записано в виде

(/2 — їх) ю2 + tnlqSl = 0.

Из этого соотношения следует приближенная формула для критической угловой скорости крена, при которой возможна потеря устойчивости движения самолета по углу скольжения (по рысканию):

(6.11)

Аналогично, если степень статической устойчивости самолета по углу атаки много меньше устойчивости его по углу скольже­ния (т. е. можно считать, что во время движения Р ^ 0), то усло­вие нейтральной устойчивости движения по углу атаки самолета, вращающегося по крену, запишется в виде равенства

(Iy — /*) О)2 + = 0,

откуда легко получить приближенное выражение для критиче­ской угловой скорости крена, при которой возможна потеря устойчивости движения самолета по углу атаки (по тангажу):

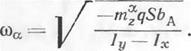(6.13)

Во всех приведенных ранее рассуждениях существенным было принятое за основу исходное движение самолета, при котором самолет вращается относительно вектора угловой скорости и как бы «проскальзывает» по некоторому конусу, образованному вра­щением оси ОХ вокруг вектора скорости, соответствующему в примере с движением по скольжению неизменному углу атаки, а в примере с движением тангажа — неизменному углу скольже­ния. Для того, чтобы такое исходное движение могло возникнуть, необходимо, чтобы величина собственной частоты колебаний са­молета (в примере с движением по углу скольжения это частота продольных колебаний, а с движением по углу атаки — частота боковых колебаний) была значительно больше угловой скорости. Нетрудно убедиться, что формулы (6.11) и (6.13) после приведе­ния их к безразмерному виду совпадают с выражениями (6.7) и (6.6) для асимптот.

Построение областей устойчивости на плоскости параметров

/п“б и mff удобно при анализе устойчивости, когда параметры летательного аппарата либо не определены, либо могут в неко­тором диапазоне варьироваться. В тех же случаях, когда аэро­динамические параметры самолета заранее определены, для ана­лиза устойчивости удобно провести построение графика зависи-

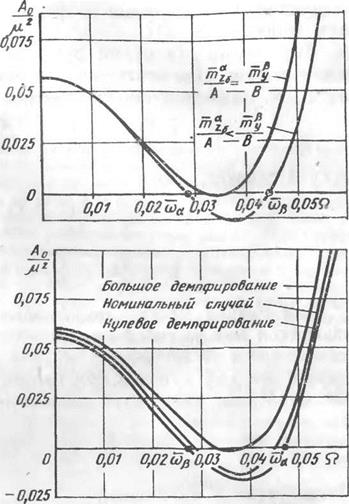
Рис. 6.3. Пример зависимости свободного члена характеристи­ческого уравнения А0 (Q) от

Р"4

соотношения запасов продоль­ной и путевой устойчивости са­молета

Рис. 6.4. Пример зависимости

свободного члена —^ А0 (Q) от ве — Ц

личин аэродинамического демп­фирования самолета мости А0 (Q), используя одно из условий (5.11). На таком гра­фике особенно четко виден смысл введенных ранее критических угловых скоростей крена. Поскольку А и В положительные числа, то для статически устойчивого самолета всегда выполняются соотношения

Л0 (0) > 0; Л0(О^оо)>0. (6.14)

С другой стороны Aq (Q2) является параболой по переменной х = Q2, которая, как это следует из выражений (6.10), может иметь либо два, либо ни одного нуля, либо один нуль в особом случае касания кривой Л0 (Q2) оси абсцисс. В качестве примера

на рис. 6.3 и 6.4 построены зависимости — Д — А0 (Q) для различ-

ных соотношений между т% и Щ и разных коэффициентов демп­фирования. Из этих рисунков, видно, что введенные ранее с по­мощью соотношений (6.6) и (6.7) критические угловые скорости

крена соа, сор соответствуют нулям функции А0 (Q), в которой все члены демпфирования равны нулю. При реальных значениях коэффициентов демпфирования, когда самолет не имеет демпфе­ров колебаний, приближенные значения критических угловых
скоростей, определенные ПО формулам (6.6) И (6.7), близки К ну­лям функции Л0 (Я).

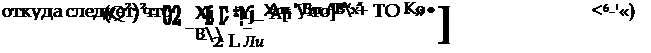Выражение для нулей функции А0 (Я) может быть получено в явном виде. Для этого, рассматривая в качестве искомого пара­метр Я2, преобразуем выражение для А0 (Я) к виду

(6.16)

Для случая малого демпфирования при существенно разли­чающихся между собой значениях критических скоростей крена из формулы (6.16) можно получить уточненное приближенное выражение для критических скоростей крена в удобном для вы­числений виде. Используя введенные ранее обозначения, запишем

Пренебрегая в соотношении (6.16) малым членом

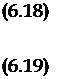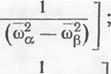радикалом и сохраняя только первый член представления квадрат­ного корня в виде ряда Тейлора, получим

Формулы (6.18) и (6.19), с учетом сделанных ранее замечаний о малости демпфирования, хорошо согласуются с расчетом. Из этих формул, в частности, видно, что демпфирование сближает

нули функции Л о (Я). Например, в случае, когда > сор, из выражений (6.18) и (6.19) следует, что

6р С сор; юа > 6)а. (6.20)

Поскольку величины коэффициентов демпфирования обычно малы, то условия устойчивости самолета могут быть записаны в виде неравенств, из которых следует, что движение устойчиво в тех случаях, когда угловая скорость крена лежит вне зоны критических угловых скоростей:

Я<:шіп(й£, сор),

либо

Q^max(coa, сор). (6.21)

В соотношении (6.21) знак min означает меньшее, а знак max большее из двух сор, которые являются нулями функции Aq (Q).

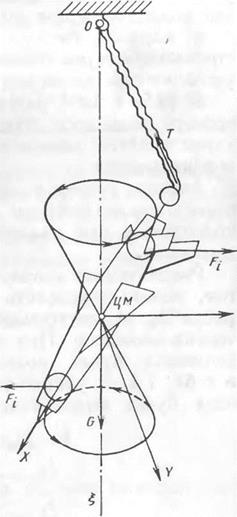
Хорошей иллюстрацией отмеченных ранее явлений может быть простой опыт с моделью самолета. Модель самолета, основная масса которой сосредоточена в фюзеляже, подвешивается на резинке, так что вес модели компенсируется силой натяжения резины. При отклонении на углы аир модель будет совершать ко­лебания относительно центра масс под действием восстанавливающей силы Т, равной весу модели (рис. 6.5). Закрутим резину и отпустим модель. При слабой закрутке резины модель самолета будет медленно вращаться относительно глав­ной оси инерции 0ХЪ почти не отклоняясь от вертикали. Если резина предва­рительно сильно закручена, угловая скорость вращения модели будет большой и достигнет критической величины, при этом пространственный «угол атаки» начинает возрастать и модель, вращаясь, «описывает» в пространстве конус, т. е. наблюдается как бы потеря устойчивости движения «в малом».

Такое движение модели близко к движению самолета при установившемся вращении по крену с той лишь разницей, что степень устойчивости у модели при движении относительно осей 0Y и 0Z одинакова, а у самолета она обычно раз­лична.

Отметим, что угловая скорость вращения модели после достижения кри­тического значения практически не возрастает, так как изменение пространствен­ного «угла атаки» модели в области критической скорости действует подобно центробежному регулятору (регулятору Уатта).

При увеличении угловой скорости «угол атаки» возрастает, что приводит к увеличению момента инерции груза на резине относительно оси 0£ и собственно тормозит развитие угловой скоро­сти вращения.

Проведенный анализ позволяет сде­лать следующие выводы.

1. Движение аэродинамически устой­чивого самолета при вращении с угло­вой скоростью крена может стать не­устойчивым в некотором диапазоне значения угловой скорости.

2. Потеря устойчивости обусло­влена действием на самолет дестаби­лизирующих инерционных моментов, возникающих при его вращении отно­сительно оси, не совпадающей с глав­ной осью инерции.

3. Для правильного анализа дина­мики самолета при движении, сопро-

Рис. 6.5. Иллюстрация движения самолета при установившемся вращении по крену на опыте с моделью самолета

вождающемся вращением относительно продольной оси, необхо­димо рассматривать нелинейные уравнения пространственного движения с сохранением членов, содержащих произведения пара­метров движения на угловую скорость крена.