Биномиальное распределение

Биномиальное распределение имеет большое применение при изучении вопросов надежности авиационной техники. Этот вид распределения относится к распределениям случай­ных величин, которые имеют в результате опыта только два несовместных исхода, например отказ — неотказ, запуск —- незапуск.

Допустим, что мы производим запуски двигателей на трех однотипных самолетах, каждый из которых оборудован одним двигателем. Нам нужно определить, какова вероятность за­пуска трех двигателей из трех с первой попытки, двух двига­телей из трех с первой попытки, одного двигателя из трех с первой попытки, ии одного двигателя с первой попытки. Здесь мы имеем дело с независимыми, противоположными события­ми и событиями, образующими полную группу.

Обозначая через А и А запуск и незапуск двигателя, через А, Ль Л2, Л2, Аз, Аз запуски и незапуски двигателей соответ­ственно на первом, втором и третьем самолетах, через В0, Ви В2, Вз незапуск ни одного двигателя из трех, запуск одного из грех, запуск двух из трех и запуск трех из трех.

Тогда события В0і Ви В2 и Вз можно сформулировать сле­дующим образом:

1. Запуск ни одного двигателя из трех не произойдет тог­да, когда с первой попытки не запустятся двигатели на первом,
«и» на втором, «н» на третьем самолетах. Поскольку союз «и» соответствует действию умножения, то

Bq = і4іА% — Ag.

2. Запуск только одного двигателя из трех может произой­ти тогда, когда запустится двигатель на первом самолете «н» не запустятся двигатели на втором «и» третьем самолетах, «или» запустится двигатель на втором самолете «и» не запус­тятся двигатели на первом «и» на третьем самолетах, «или» запустится двигатель на третьем самолете «и» не запустятся двигатели на первом «и» втором самолетах. Это сложное со­бытие можно математически записать так:

Вх — Лі А% As ~Ь Ах As As "і* А А $ А%.

3. Запуск двух двигателей из трех может произойти тогда, когда запустятся двигатели на первом «и» втором самолетах «н» не запустится двигатель на третьем самолете, «или» за­пустятся двигатели на первом «и» третьем самолетах, «и» не запустится на втором, «или» запустятся двигатели на втором «и» третьем самолетах «и» не запустятся на первом:

В2 = А Аг Aq — f Ai Л2 <43 4~ Ах А2 ^э.

4. Запуск двигателей произойдет на всех трех самолетах:

Bg = Ai А2 As.

Используя теоремы сложения и умножения вероятностен, мы можем записать для событий В0, Ви -62, В% их вероятности, если нам заранее известна Р — вероятность успешного запус­ка при каждой попытке. Обозначая Ро, з; Pi#; Рг, з; Рз, з как вероятности успешных запусков из числа запускаемых двига­телей, запишем вероятность незапуска ни одного двигателя из трех:

Р(Во) — Яо. з = Р(АгАиАг) = P{Ai)P[A*)P(As) =

— О —p)(i — p)(i —р) = (1

Вероятность запуска одного двигателя из трех:

P(Bi) = Рі. з — Р{АХ А2 4* Ах Az As 4- Ах А2 Лв) =

“ Р (^i А2 Л8) 4* Р(А А^ /4з) 4- Р{А А2 Ад) =

— Р(Аг)Р(А,)Р(А3) + Р(АХ) РШ Р Из) + Р (А,) Р (А,) Р (As) —

/>0-/00- Р) ‘і-(* —/?)Р(1 p) -И1 — Ж1 -/>)/> =

= 3/7(1 р)

Вероятность запуска двух двигателей из трех:

Г (В,) = Рад = Р (Л, 4, А3 + Л, Л2 Ла + А, Л3 Л3) = 3 (1

Вероятность запуска трех двигателей из трех:

P(BS) = Р,,3 = Я (Л» Л2 л3) = рг.

Решим подобную задачу в общем виде. Для этого обозна­чим через Ртлп вероятность того, что на п самолетах {п по­пыток) будет т успешных запусков двигателей с первой по­пытки:

1 Іапрнмер, п — 5, т~ 3, тогда

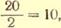п

т(п— т)

а Рз,5 = 1 Ор8 (1 ~~р)2; или «~8; т ~ 3, тогда

Число т успешных запусков в серии из п попыток (опы­тов) является случайным. Это число может принимать сле — іующиє значения 0; 1; 2; …; п—1; п с соответствующими ве­роятностями Ро, л, Pi. и, Р%п,. — —

Таким образом, уравнение (2.7а) определяет собой распре­деление вероятностей случайного числа т, которое называет­ся биномиальным.

Из уравнения следует, например, что Ро, п — (1 — Р)п Р, ип — Рп, так как Спп = 1 и С« = 1, если принять 0! за еди­ницу.

2.5. Случайные величины

Характеризовать ту или иную конечную совокупность опы­тов мы можем не только отвечая на вопрос, что произошло в процессе опыта, но также отвечая на вопросы, когда произо-

шло интересующее нас событие в каждом из N проводимых опытов, сколько раз появилось это событие в N опытах и т. д. Иными словами, продолжая анализ опыта, теория вероятнос­тей дает его количественную характеристику и вводит новое понятие случайной величины.

Случайной величиной называется величина, которая в ре­зультате опыта может принимать то или иное значение, при­чем заранее до опыта неизвестно какое именно.

Случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить, называются прерывными или дискретными случайными вели­чинами.

Случайные величины, возможные значения которых не­прерывно заполняют некоторый промежуток, называются не — прерывными случайными величинами.

Случайная величина характерна тем, что она в результате опыта принимает некоторое одно, заранее неизвестное, но единственное значение

Следует отметить, что термин «случайная величина» не совсем удачен, и более подходящим был бы термин случайная функция, независимой переменной которой является точка в пространстве элементарных событий, т. е. исход опыта.

Поэтому в литературе но теории вероятностей случайной величине часто дается определение как функции, определен­ной на пространстве элементарных событий.

Типичными примерами случайных величин могут служить следующие:

— число отказов системы, появляющихся за интервал эк­сплуатации t

■—моменты времени внезапных отказов элементов на вре­менном интервале от 0 до /;

— моменты времени отказов из-за износа, которые прак­тически появляются, в отличие от внезапных отказов, на ко­нечном временном интервале.

Случайная величина наиболее полно может быть охарак­теризована ее законом распределения, представленным в од­ной из следующих форм:

— для дискретной случайной величины:

1) функции распределения:

2) ряда распределения;

— для непрерывной случайной величины:

1) функции распределения;

2) плотности распределения.

каждая из форм закона распределения представляет со — їм>и некоторую функцию, которая полностью описывает слу-

…. .. величину с вероятностной точки зрения.

II общем случае функция распределения случайной вели­чины А’ есть вероятность события Х*Сх и обозначается F(x),

I V

F(x) = P(X<x),

іде х — текущая переменная; X — случайная величина.

Производная от функции распределения непрерывной слу­чайной величины X называется плотностью распределения или плотностью вероятности /(*):

f{x)^F'{x),

іде f(x) —плотность распределения; F(x) —функция распре­деления.

Для дискретной случайной величины X функция распреде­ления

/^(л) — является ступенчатой функцией,

все х*х а ряд распределения

(2.8)

f(x) = P(X^x).

Для непрерывной случайной величины X функция рас­пределения

F(x) = j’ f(x)dx.

Кроме функции н плотности распределения (плотности ве­роятности) , случайную величину можно до некоторой степени, достаточной для решения ряда практических задач, охаракте­
ризовать с помощью нескольких числовых параметров. Важ­нейшими из них являются следующие:

— среднее значение случайной величины (математическое

ожидание) *ср;

— дисперсия случайной величины О(Х);

— среднее квадратическое отклонение о.

Среднее значение случайной величины характеризует по­ложение случайной величины на числовой оси, т. е. указывает некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины. Термины среднее значение или математическое ожидание слу­чайной величины Л’ являются синонимами и обычно обозна­чаются хср или М(Х).

Среднее значение случайной величины вычисляется по формулам:

— для дискретной случайной величины

*сР = 2 (2.Ю)

/=і

— для непрерывной случайной величины

хср — J xf(x) dx. (2.10а)

— Об

Для характеристики разброса случайной величины X от­носительно ее среднего значения хср служат дисперсия D(X) и среднее квадратическое отклонение о. Дисперсией случай­ной величины X называется среднее значение квадрата откло­нения случайной величины от ее среднего значения.-

Среднее квадратическое отклонение представляет собой среднее значение абсолютной величины отклонения случайной величины от ее среднего значения.

Дисперсия и среднее квадратическое отклонение случайной величины вычисляются по формулам-

D(X)_ £ to — *ер ГР-

I

(2.11)

і тх);

для непрерывной случайной величины

D(X)=~ j {х — xcp)2f(x)dx

(2 Л 2)

о ~ Vd(x) .

Усложнение вычислений среднего квадратического откло — ік’ішя случайной величины о путем извлечения квадратного корня из дисперсии объясняется тем, что среднее значение ■пклонеиия случайной величины от ее среднего значения всег — UI равно нулю.

Пример 2.8. Допустим, что среднее время, потребное на выполнение регламентных работ, равно:

100-часовых — 10 час;

200-часовых— 18 час;

000-часовых — 48 час.

Требуется вычислить среднее время выполнения регла­ментных работ, если средний налет каждого самолета в год равен 300 час.

Решение. 1. Введем следующие обозначения: zu z^

1, — соответственно числа 100-, 200- и 600-часовых регламент­ных работ, выполняемых на каждом самолете за 300 час на­їв га в год; z — суммарное число регламентных работ, выпол­няемых на каждом самолете в год; щ, Пг, «з — вероятности пребываний самолета на регламентных работах каждого вида (І00-, 200- и 600-часовых);

2. Определяем Zy г2, z3 и z:

^ 600 0,5: г’ 200 0,5 “ 1;

г, =-у—-0,5-1 = 1,5; 2=0,5+1 + 1,5 = 3.

3. Вероятности щ, и.2 и из определяются как отношение произведения среднего времени выполнения регламентных ра­бот каждого вида и числа регламентных работ каждого вида, выполняемых на одном самолете (г£тД к сумме этнх произве-

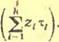
и, можно рассчитывать по

ziri

h

Ъг‘~;

І— 1 где zt — среднее число регламентных работ /-го вида на од­ном самолете; — среднее время выполнения регламентных работ /-го вида на одном самолете; k — индекс для старшего вида регламентных работ, т. е. регламентных работ, выполня­емых через наибольшие интервалы наработки;

-і м — 1,5*13= 19,5 час: т2 = 1 — 20 = 20 час;

zs~.s = 0,5-48 = 24 час;

"‘=тй—°’307; "^W=°’3I5;

24

"’=«sr°-37a

4. По формуле (2.10) определяем среднее значение време­ни выполнения регламентных работ всех видов:

~ср = 0,307-13 + 0,315-20 4- 0.378-48 = 28,4 час.

Пример 2.9. В течение года на самолетах авиационной группы 100 раз выполнялись регламентные работы (100-ча­совые). Хронометраж показал, что в 40 случаях выполнения регламентных работ потребовалось затратить время 16 час, в 30 случаях — 18 час, в 20 случаях — 20 час и в 10 случаях — 22 час. Также из опыта известно, что выполнение этих регла­ментных работ физически невозможно за время меньше 14 час, т. е. *о=14 час.

Требуется определить функцию распределения времени выполнения 100-часовых регламентных работ.

Решение. 1. Вычисляем среднее время, дисперсию и среднее квадратическое отклонение времени выполнения ре­ма ментных работ:

*ср « 0,4* 16 + 0,3-18 + 0,2*20 + 0,1 -22 = 18 час

/;(/рр) = (16- 18)80,4 + (18- 18)2-0,3 + (20- 18)2-0,2 +

+ (22 18)2-0,1 = 4 час.

а — 2 час.

2.

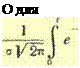Из условия задачи видно, что в качестве распределения времени выполнения регламентных работ можно принять нор­мальное распределение, а вероятность выполнения регламент­ных работ в течение времени t определять формулой

где G(t) — вероятность выполнения регламентных работ; t — текущее время выполнения регламентных работ; tG — мини­мально возможное время выполнения регламентных работ. (Это время получено из опыта работы технического состава данной авиационной группы).

Таким образом, для нашего примера функция распределе­ния времени выполнения регламентных работ будет иметь следующий вид:

о (о = і — «г[1]*’,

Функции распределения времени работ, встречающихся прй техническом обслуживании летательных аппаратов. 1. При выявлении и устранении отказов время выполнения работ распределено по закону, который не противоречит показатель­ному закону

где t — время выявления и устранения отказов; р — интен­сивность выявления и устранения отказов; G{t)—вероят­ность выявления и устранения отказов за время t.

2. В условиях проведения всех видов подготовок к полетам (за исключением предполетной подготовки) и выполнения регламентных работ инженерно-технический состав имеет дело с неисправными самолетами, что обусловливает выявле­ние и устранение отказов. Поэтому объем подготовок, регла­ментных работ носит случайный характер с нормальным рас­пределением продолжительности подготовки, выполнения регламентных работ и G(t) определяется по формуле

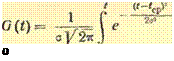(2.16)

где G(t) — вероятность выполнения работ по подготовке са­молетов к полету (выполнения регламентных работ) за вре­мя t; tcр — среднее время выполнения работ; о — среднее квадратическое отклонение времени выполнения работ.

3.В некоторых случаях для упрощения расчетов выби­рают «смещенное» показательное распределение продолжи­тельности подготовок с параметрами

Рі в ~ і *о. — ^ср 6),7 з.

Тогда G (I) определяется по формуле

где G (/) — вероятность подготовки самолетов (выполнения регламентных работ) за время t; и /о, — параметры под­

готовки, вычисленные по формулам (2.17).

Г. ікіім образом, для планирования всех видов работ по ‘чническому обслуживанию и войсковому ремонту самолетов Н’дует использовать формулы (2.5) — (2.8).

Расчет р, и t0t производится по формулам (2.17). Значе­ние tcp и о определяют из статистики техническою обслужи — ц и имя самолетов. Следует заметить, что величины /ср и з ‘•V іут характеризовать не только эксплуатационное совершен­ию конструкций летательных аппаратов (восстанавливае­мость), но также уровень квалификации инженерно-техннче — •кого состава и условия его работы (базирование, климат, игография и т. д.).

Пример 2.10. Из опыта подготовок самолетов к полету из­вестно, что среднее время подготовки tcp = 6,5 час; а среднее квадратическое времени подготовки о» 1,5 час. Определить (i(t) за время t~7 час.

Решение. По формулам (2.7) рассчитываем:

Р, = = 0,665 1}час

К — tcp — 0,7 о » 6,5 — 0,7* 1,5 = 5,45;

О (7) = 1 — г0,665 {7“5,45) 1 — е~ш = 1 0,357 = 0,643.

Это значит, что за время /— 7 час из 100 подготовок будут выполнены 64 подготовки. Остальные 36 подготовок будут выполнены за время, большее 7 час.

4. Для упрощения вычисления вероятностей случайных ве­личин, распределенных не по показательному закону, приме­няется распределение Эрланга.

Допустим, что отказ или восстановление элемента насту­пает в результате прохождения k стадий, причем длитель­ности /], …,/* этих стадий будут независимыми показательно распределенными случайными величинами с плотностью рас­пределения цув’ Предполагаем, что в конце первой стадии

по истечении времеин ti начинается вторая стадия и т. д. От­каз (восстановление) наступает в конце &-ой стадии. Таким образом, время безотказной работы (время восстановления) / равно /і + …+ tk, а плотность распределения времени Нравна

/*(*) = і (со/)*-*

k — 1)!

	—Olt