ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ

Полученные в предыдущем параграфе математические модели про­странственного движения самолета в виде систем дифференциальных урав­нений являются нелинейными. Их решение как аналитическими, так и численными методами затруднено. Однако если принять допущение о том, что значения параметров движения самолета в возмущенном движении отклоняются на малые величины по отношению к тем значениям этих параметров, которые имели место до начала действия возмущений, то появляется возможность перейти от нелинейных моделей к линейным.

На этом допущении базируется идея метода малых возмущений, позволяющего рассматривать возмущенное движение самолета как сово­купность опорного (невозмущенного) движения и движения под действием малых возмущений.

Примем допущение о малой продолжительности переходных процессов при возникновении возмущений. На этом допущении базируется идея метода «замороженных коэффициентов». Сущность этого метода состоит в том, что отрезок времени I, в течение которого происходит исследуемое движение, разбивается на отдельные интервалы. На этих интервалах коэффициенты уравнений принимаются постоянными и равными их значе­ниям в начале интервала. Тогда математическая модель будет состоять из совокупности дифференциальных уравнений с постоянными коэффициен­тами, причем число таких уравнений равно числу интервалов времени.

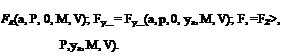Линеаризованные уравнения собственного поступательного движения. Рассмотрим нелинейную математическую модель собственного поступа­тельного движения в виде системы динамических уравнений (2.10). Анализ правой части уравнений показывает, что проекции вектора сил FK на оси траекторией системы координат Fx, Fy, являются нелинейными функциями параметров движения самолета и параметров окружающей среды. Пренебрегая изменением с высотой плотности воздуха р„, давления ря и температуры Тн, с достаточной для практики точностью приближения эти функции можно представить следующим образом:

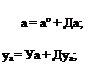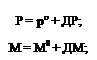Применим метод малых возмущений для линеаризации уравнений (2.10) с учетом зависимостей (2.24). Параметры возмущенного движения выража­ются через параметры опорного движения а°, Р°, 9°, уа, М°, V0 и малые отклонения параметров возмущенного движения от их значений в опорном движении Да, АР, ДО, Дуа, ДМ, AV:

Рассмотрим первое из динамических уравнений (2.10) поступательного движения самолета относительно траекторной оси ОХа

dV

т — =FX(«, Р, 0, М, V). (2.26)

ui ‘

Опорному движению соответствует одно из частных решений уравнения (2.26) V = Vе. Если подставить это частное решение в (2.26), то получим уравнение, отвечающее опорному движению:

dV°

т —— = F. (а, Р°, 0°, М°, V°). (2.27)

ПГ "

Вычтем из уравнения (2.26) уравнение (2.27): dAV

Разложим нелинейную функцию Fx (а, р, О, М, V) в ряд Тейлора по степеням вариаций Да, Др, Д6, ДМ, ДУ в окрестности значений а°, р°, 9°, М°, Vе:

FXi(ct, р, в, М, V) = FXj (a0, р°, 0°, М°, V0) +

+ F; Да + F^ Др + F^A0 + F“ ДМ + F* ДУ + Fx (Да, ДР, Д0, ДМ, ДУ),

(2.29)

.{Щ

SaJ, производные, взятые в бкрестности опорного движения, которые определяются по формулам табл. 2 приложения с учетом (1.13); Fx (Да, др, Дв, ДМ, AV)-совокупность членов разложения выше первого порядка малости.

Подставим разложение (2.29) в уравнение (2.28) и получим линейное динамическое уравнение поступательного движения самолета относительно траекторной оси ОХс:

тДУ = F£ Да + F^ ДУ + f“ ДМ + Fx_ Д0 + Fx Др. ‘ (2.30)

Аналогичным образом проведем линеаризацию динамического уравне­ния поступательного движения самолета относительно траекторной оси OYK (2.10): ‘

mV0 ДА = F“ Да + F^AV + F. M ДМ + F; Д0 + F* ДР + F;; Ду. (2.31)

Коэффициенты уравнения F“t, Fy, Fy“, F^, F^, Fy* приведены в табл. 2 приложения.

Для динамического уравнения поступательного движения самолета относительно траекторной оси OZK (2.10) получим следующее линеаризо­ванное уравнение:

— mV° cos 0° Д* = F“ Да + F* Д V + F™ ДМ + f£ Д0 +

+ F*AP + F**Ay.. (2.32)

Коэффициенты уравнения F?, F^, F£ , F^, F£, F£ приведены в табл. 2 приложения.

Линеаризуем кинематические уравнения поступательного движения самолета (2.11). Для опорного движения вдоль траекторной оси ОХк

dL°

= У° соз 0° cos Ч*0. (2.33)

dt v ’

Для возмущенного движения

d (1

— (L° + AL) = У° cos о° cos Т°—— : (V СОЗ 0 cos ¥)„ ДУ+

at dV

d d

+ — (Vcos 0cos’P) Д0 + — (Vcos 0cos¥)0A4′ . (2.34)

ao от

Вычтем из уравнения (2.34) уравнение (2.33):

ДЇ. = cos 0° cos ‘Р0 AV — V cos’?0 sin 9° Д9 — V cos 0е sin Т0 Д*Р. (2.35)

Аналогичным образом выполним преобразования для двух других уравнений (2.11):

ДН = sin 0° ДУ + V® cos е° Д0 ; (2.36)

Дг = V0 sin0° sin’РДР — cos 0° sin*?0 AV — V0 cos 9° cos’?0 ДТ. (2.37)

Линеаризованные уравнения собственного вращательного движения.

Нелинейная математическая модель собственного вращательного движе­ния самолета содержит систему динамических уравнений (2.16) и систему кинематических уравнений (2.19). Анализ правой части динамических jypae- нений показывает, что проекции вектора результирующего момента MR на оси связанной системы координат Мх, Му, MR> являются нелинейными фукциями параметров движения самолета и управляющих воздействий. Эти функции с достаточной для практических задач точностью можно представить следующим образом:

Выразим параметры возмущенного движения через параметры опор­ного движения ®°, ®!, со!, й° и малые отклонения Д®х, Д®у, Д®г, Да:

®х = ю! + Д®„; ®у = ®у + Д®у; юг = ®! + Д®х; а = й0 + Да

Рассмотрим первое из динамических уравнений (2.16) вращательного движения относительно оси ОХ. Опорному движению соответствует одно

из частных решений уравнения (2.16) для юх = ю! и юу = ®!. Если под­ставить это частное решение в (2.16), то получим уравнение, Отвечающее опорному движению:

і О * О

+ ~ 1у)(0у(°° + Ky(0°Wy ■ М-(а°’ V°’ (2-39)

В ближайшей окрестности опорного движения

d н

J* dt — Ю’°+ ~ J*y dt+ + ljj “ VK + Дшу^ш° + А“г) +

+ JXy (®! + Д®х) (со! + Д® ) = Мх(а0, V0, р°) + м! Да + Мх Д V +

+ М“* Дюх + М“’Д®у + Мх АР + Мх (Да, ДУ, Д®х, Дсоу, ДР), (2.40)

" ‘ да ‘ V ——- . ч—ч™,,

водные, которые взяты в окрестности опорного движения с учетом (1.23) и приве­дены в табл. 3 приложения; Мх(Да, ДУ, Д<ох, Дсоу, Д0)-совокупность членов разложения выше первого порядка малости.

42

Вычтем из уравнения (2.40) уравнение (2.39) и получим линейное динамическое уравнение вращательного движения самолета относительно связанной оси ОХ:

Jx Аюх — Jxy Асоу = М“ Да + Мх AV + М“* Аюх + Мху Аюу + Мх Ар.

Х. — (2.41)

Аналогичным способом проведем линеаризацию динамического уравне­ния вращательного движения самолета (2.16) относительно связанной оси Оу: __

Jy Дйу — Jxy A<bx = М“ Аа + Му AV + М^* Аюх + М“’ Асау + Му Ар,

(2.42)

где коэффициенты уравнения Kfc.’My взяты в окрестности опорного

движения и приведены в табл. 3 приложения.

Для динамического уравнения вращательного движения самолета относительно связанной оси OZ (2.16) получим следующее линеаризован­ное уравнение: ;

Jz Acbz = Mr* A©z + Mr Аа + Mr AV + Mr АМ + Mr Ар,

‘ ‘ ‘ * * (2.43)

где коэффициенты уравнения Mr Mr, Mr, М£ , М^. взяты в окрестности опорного движения и приведены в табл. 3* приложения. ‘

Аналогичным образом выполняют линеаризацию кинематических уравнений вращательного движения (2.19), для которых, пренебрегая величинами второго порядка малости, получим:

Ду = (оо“ sin у0 — га" cos у0) Ao/cos2 и° + ск — tg и° cos у0 Асоу; (2.44)

Ао = cos у° Acoz + sin у° Асо + (ю° cos у° — <я° sin у°) Ду; (2.45)

Д|/ = — sin у0 Acoz/cosu° + Юу cosy" tgu0At>/cosi)° + cosу°Дюу/со8 0° —

— (raj sin у0 + (о° cos у°) Ay/cos u°. (2.46)

Линеаризованные геометрические соотношения между углами, опре­деляющими положение самолета в различных системах координат (2.20), с учетом пренебрежения величинами второго порядка малости принимают вид:

COS Y° rCOS 9°

Да= ——- — ————- (cos о0 cos (*P — |/°) Au — cos и0 A0 + sin (XF°- }/°) Ay);

cos a0 cos P°

te v° cos u° cos p° AP

Aw = tg y° cos о Аи — A0—————————— —

cos (4*° — v°) cos 0° cos y° cos (XP°

(

cos u°

sinn0 — tg0“ —————— — 1 Ду;

cosCP0-

(—cosv>°cosa°8x р° сову0 Да + cosa°cosi)0 smP°Ai) +

+ СО8 Р° (СО8 а° Sin 0° — CO8U0 С08 у° Sin а°) АР + СО8 0° С08 Р° С08 у° Ду) .

(2.49)

Таким образом, линеаризованная математическая модель собственного движения самолета характеризуется уравнениями (2.30)—(2.32), (2.35)- (2.37), (2.41)—(2.49).

Линеаризованные уравнения полного вынужденного пространственного движения. Проведем линеаризацию математической модели вынужденного движения самолета (2.21) с учетом того, что проекции вектора сил F, на оси траекторной системы координат следующим образом зависят от пара­метров управляющих и возмущающих воздействий:

РХ, = Fx_ (5Х, §у, 5Р, fx, fy, aw, Pw)l

Fy. = Fy>(5x, 5y, S„ 5P, fx, fy, fz, aw, pw); (2.50)

Pz, = Pz,(Sy> 5Z, 5P, fy, iz, aw, Pw).

Тогда для динамического уравнения поступательного движения относи­тельно оси ОХх с учетом уравнения собственного движения (2.30) получим

mAV = F“ Да + F* AV + Fx^ ДМ + Fx> А0 + F* ДР +

X Я X Г Ґ

+ F;; А8Х + F^ А5у + Р А5Р + ^ Afx + F;^ Afy +

+ F^Aaw + F^Apw. (2.51)

Я К X Г Г Л л

Коэффициенты уравнения F“ F"y, F^, , F“w, F£ приведены в табл.

4 приложения. ‘ * *

Динамическое уравнение поступательного движения относительно траекторной оси OYK с учетом уравнения собственного движения (2.32) имеет вид

mV0 А0 = F; Да 4F’ AV + F, M ДМ + F”y> ДО + F^_ Др + Fj; Ауа +

+ F*; А5Х + F*; А5У + F^; A5Z + ^ А5Р + Ff — Afx +

+ F^’ Afy + F^ Afz + F! w Aaw + F^ APw. (2.52)

Коэффициенты уравнения F£, F£, F"_’, F®", F£, F£, Fz“, F“w, Р^*приведены в табл. 4 приложения. * ‘ *

Для динамического уравнения поступательного движения относительно траекторной оси OZx с учетом уравнения собственного движения (2.32) получим

— mV° cos 0° At = F“ Да + F^ AV + F™ ДМ + F; ДО +

44 …

Коэффициенты уравнения Fz’, Fz F^, F^, F^, F“w, Fz* приведены в табл.

4 приложения. .

Уравнения (2.35)-(2.37) остаются без изменений.

Для динамических уравнений вращательного движения учтем следую­щие зависимости проекций вектора результирующего момента MR от управляющих и возмущающих воздействий:

Мх = МХ(8Э, 8Н, тхв, aw, pw);

Му = Му(8э, 5Н, myB, aw, pw); (2.54)

MRz = MRz(8B, 5p, ф, rnZB, aw, Pw).

Тогда для динамического уравнения вращательного движения относи­тельно оси ОХ с учетом уравнения собственного движения (2.41) получим

Jx Acbx — Jxy Дюу = М? Аа + Мх AV + М“” Аюх + Мх’ Аюу +

+ М. р АР + М“* А5Э + М“- А8„ + М”“ AmXB + М7 Aaw + Apw.

(2.55)

Коэффициенты уравнения Мх’, Мх“, М™", M“w, Mxw приведены в табл.

5 приложения.

Динамическое уравнение вращательного движения относительно оси ОУ с учетом уравнения собственного движения (2.42) имеет вид

Jy АсЪу — Jxy Аюх = М“ Аа + Му AV + М“ж Аюх + Му’ Ашу +

+ Мур АР + Му* А5Э + Мр А8Н + М™” Amy„ + M.“w Aaw + MPw Apw.

. . „ (2-56)

Коэффициенты уравнения Му’, М““, М™’", Му", Му приведены в табл. 5приложения.

Для динамического уравнения вращательного движения относительно оси О2 с учетом уравнения собственного движения (2.43) получим

Jz Acoz = Mr’ Ao)z + MRj Аа + MRi Аа + M^AV + Mr* АМ + MRi Ар +

+ MR^ A8B + MR^ Atp + MRj Д8Р + MR" ArnZB + MRwAaw + MR" Apw.

’ 1 * 2 ‘ ‘ (2.57)

Коэффициенты уравнения Mfe",, Mr, N4:, K", K", Mrw приведены в табл. 5 приложения.

Система линеаризованных кинематических уравнений Вращательного Движения самолета (2.44)-(2.46) остается без изменений.

В линеаризованных геометрических соотношениях учтем составляющие ветра:

COS Y° cos 0°

Да = Да», + —— — —— — (cos и° cos (Ч"1 — vj/°) Ди — cos о° Д0 + sm (Т° — ц/п) Ду);

Таким образом, линеаризованная математическая модель вынужден­ного движения самолета содержит уравнения (2.35)-(2.37), (2.44)-(2.46), (2.51)-(2.53), (2.55)-(2.59).