УРАВНЕНИЯ ПРОДОЛЬНОГО И БОКОВОГО ДВИЖЕНИЯ

Уравнения собственного продольного и бокового движения. Представим математическую модель полного собственного движения самолета в про­странстве состояний в виде следующего векторного уравнения:

*п№~1 Гап А6п 1 Г хп(t) 1 М*>-1 1-Ап6 А6 J |_x6(t) J

Вектор-столбец переменных состояния продольного движения само­лета

[хп (t)]r = [Аса,(t) Аа(0 Ли (I) AV (t), А0 (I) АН (I) AL(t)]. (2.102)

Вектор-столбец переменных состояния бокового движения самолета [x6(t)]T = [Дсох(1) Дшу (I) Ар (I) Ау (t), Ay (I) A¥(t) Az(t)]. (2.103)

Матрица состояния продольного движения самолета

агаг, шг аюг, а aa>z, u arnz, V 0 0 0 ао, ш1 аа, а аа, и aa, V 0 0 0 аи,0), 0 0 0 0 0 0 0 aV, а aV, u avV 0 0 0 0 а8,а ae. u ae V ae, e 0 0 0 аН, а aH, и aH, V 0 0 0 0 0 0 & r <  aL, t) 0 0

А

(2.104)

 

а0>„Юу аю„Р 0 0 0 0 агау, йу а(0у, Р 0 0 0 0 аР>®, аи, р 4-і 0 0 0 а7,а>, VJ 0 0 0 0 аЧ1,ш, ° а¥.у 0 0 0 п и а^а ат у 0 0 0 0 0 0 0 "„У 0

ашх, тх 4.’“. afl rrt

(2.105)

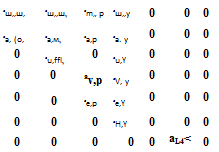Матрица состояния перекрестных связей из бокового движения в продольное.

Матрица состояния перекрестных связей из продольного движения в боковое

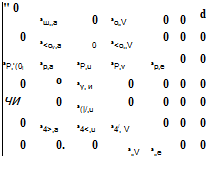
(2.107)

С формальной математической точки зрения уравнение (2.101) может быть разделено на два независимых уравнения, если равны нулю или пренебрежимо малы все элементы матриц А6п и Ап6.

Для разрежения матриц А6п и Ап6 можно сделать несколько физических Допущений. Так, если предположить симметричность самолета относи-

тельно плоскости ХОУ, то производные сил и моментов, действующих в продольной плоскости по параметрам бокового движения, будут равны нулю:

(2.108)

Это объясняется тем, что разложение сил и моментов в ряд Тейлора проводилось в окрестности опорного движения, а сами эти функции равны нулю в точке, соответствующей опорному движению в силу их симметрии. Аналогичным образом производные сил и моментов, действующих в плоскостях Х02 и YOZ, по параметрам продольного движения также будут равны нулю:

. Следующим допущением является переход к рассмотрению частного случая пространственного движения, когда самолет летит без крена у0 = О,

у а = 0. Тогда sin у° = 0 и siny° = 0. При малых углах атаки а° = 0 и sina° = 0. Если движение самолета происходит без скольжения (Р° = 0), путевой угол совпадает с углом рыскания (*F° = у°), а опорное движение

совершается с нулевыми угловыми скоростями GK = <в,° = <в° = О (прямо­линейный горизонтальный полет без крена и скольжения).

Новые выражения для коэффициентов динамических уравнений посту­пательного движения приведены в табл. 19 приложения с учетом изменив­шихся выражений для производных сил. Выражения для коэффициентов кинематических уравнений поступательного движения, динамических и кинематических уравнений вращательного движения, а также уравнений геометрических соотношений приведены соответственно в табл. 20-23 приложения.

Анализ выражений для коэффициентов показывает, что все коэффициен­ты, составляющие матрицы А6п и Ап6, тождественно равны нулю. Следова­тельно, А6п = 0, Ап6 = 0, что позволяет рассматривать продольное и боко­вое собственное движение самолета независимо друг от друга. Уравнение (2.102) распадается на два уравнения:

*„№ = А„хп№; (2.110)

Mt) = A6x6(t)

Решения уравнений (2.110) и (2.111) имеют вид:

МО = q>„(t, t0)xn(t0); (2.112)

хб(0 = Vefti to) хб(1о)’ (2.113)

где ФпР, t0), p6(t, t0)-переходные матрицы состояния соответственно продольного и бокового движения самолета.

Уравнения вынужденного продольного и бокового движения. Представим математическую модель полного вынужденного движения самолета в ’56

пространстве состояний с учетом модели собственного движения (2.101) в виде следующего векторного уравнения: ‘

Г *п(0] Гм о МО] Гву вЦ Г Mt)] Г В* ВМ1 Г МО]

LmoJ Lo mJImoJ ві J L^(t)-I L-B»6 bm Lu»(t)J

(2.114)

Вектор-столбец входа по управляющим воздействиям в продольном движении самолета

С«І(03Т = [ДМО A8,(t) A8,(t) ASp(t)]. (2.115)

Вектор-столбец входа по управляющим воздействиям в боковом движе­нии самолета

[М0]г = ОМО A8B(t) А8,(ед. (2.116)

Вектор-столбец входа по внешним возмущениям в продольном движе­нии самолета

[Un(0]T = [Afx(0 Afy(t) Ama(0 Aaw(t) Aaw(t)]. (2.117)

Вектор-столбец входа по внешним возмущениям в боковом движении самолета

[Нб(0]т = [Afz(t) AmXB(0 Атув(0 Apw(t) A$w(0]. (2.118)

Матрица входа по продольным управляющим воздействиям

(2.119)

Матрица входа по боковым управляющим воздействиям

(2.120)

(2.121)

Матрица входа по перекрестным связям продольных управляющих воздействий с параметрами состояния бокового движения

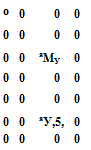(2.122)

Матрица входа по продольным внешним возмущениям

		4,^.		aMt. dw
aa, fx	aa, fy	0	ao, aw	au. d*.
0	0	0	0	о
av, f,	aV, fy	0		о
ae, f„	a9,fy	0	a9haw	о
0	0	0	aH, B*	о
0	0	0	0	о

(2.124)

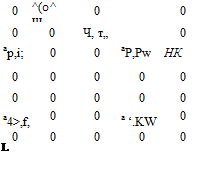Матрица входа по перекрестным связям продольных внешних возмуще­ний с параметрами состояния бокового движения

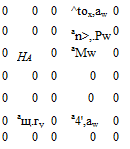(2.125)

Матрица входа по перекрестным связям боковых внешних возмущений с параметрами состояния продольного движения

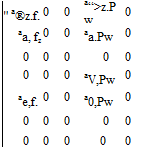(2.126)

Элементы матриц раскрыты в табл. 24 и 25 приложения.

Условием независимости продольной и боковой составляющих вынуж­денного движения самолета является равенство нулю всех элементов

матриц в£п, В„6, ВбП, Й^6. Для симметричного относительно плоскости XOY самолета это достигается в прямолинейном полете без скольжения. Тогда векторное уравнение полного вынужденного движения самолета (2.114) можно представить в виде двух независимых уравнений с новыми значениями коэффициентов, приведенных в табл. 24 и 25 приложения:

хп (I) = Апхп (I) + ВГ иу (I) + в! un(t); (2.127)

х6 (I) =А6х6 (I) + Вуб »1 (1) + Вё u6 (t). (2.128)

Решения уравнений (2.127) и (2.128) имеют следующий вид:

і

Х„ (t) = ф„ (t) Хп (0) + J Фп (t _ т) Ву иу (х) dx +

о

t

+ |<Рп(4-т)Впип(т)йт; (2129)

О

t

х« (t) = фв (t) хб(0) + J q>6 (t — т) (т) dx +

о

t

+ J Фв (t — т) Вб Иб (т) dx. (2.130)

о

Таким образом, полное пространственное движение самолета можно рассматривать как два независимых движения: продольное и боковое.