МОДЕЛИ НАДЕЖНОСТИ СИСТЕМ ВС

В тех случаях, когда для исследуемой системы (подсистемы, элемента) допускаются лишь два возможных состояния — пол­ной работоспособности и полного отказа, функционирование си­стемы моделируется с помощью булевой алгебры (75]. При этом состояния системы и каждого элемента достаточно просто опи­сываются с помощью булевых переменных, которые принимают значения 1 в случае работоспособности и 0 в случае отказа. На­дежность систем, поведение которых можно во времени интер­претировать как случайный процесс {z(f), 0} с конечным мно­

жеством состояний М — {га, z2, …, zm} и непрерывной областью изменения параметра, целесообразно исследовать с помощью 2—822 ‘ 17

марковских моделей. Напомним, что свойство марковости заклю­чается в том, что будущее поведение процесса не зависит от его прошлого, а определяется лишь настоящим.

Границы применения булевых и марковских моделей надеж­ности рассмотрим отдельно, чтобы помочь читателям при выбо­ре иных способов формализации.

Булевые модели. Положим, что система состоит ‘из п эле­ментов, при этом і-му элементу соответствует булева перемен­ная Хі, допустимыми реализациями которой являются числа 1 и 0. Тогда

1, если і-й элемент функционирует; 0, если 1-й элемент отказал,

где £=1, 2, …, п.

Булева функция определит состояние системы при помощи структурной функции работоспособности системы переменных Хи х2, …. хп, которую можно задать в виде ’

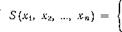1, если система функционирует; 0, если система отказала.

Работоспособность или отказ системы определяется состоя­ниями ее элементов. Существуют два предельных случая: одно­временный отказ всех элементов (система отказывает) и одно­временное функционирование всех элементов (система функци­онирует) . Остальные случаи предполагают выполнение свойст­ва монотонности, которое заключается в следующем: если си­стема функционирует, когда отказало подмножество Мі ее эле­ментов (остальное множество Mi элементов функционирует), то система обязана функционировать и в том случае, когда отка­зало лишь подмножество М2<^М элементов [19].

Изложенные состояния системы при функционировании или отказе всех ее элементов с учетом свойства монотонности можно записать так:

S(l, .., 1)=1; SCO, …. 0)=О;

Sp-1!, …. Xі п) <S (■*?!, …. х2п),

если выполняется условие Х1І < х2і i= 1, 2, …., п.

В качестве вычислительных операций над булевыми — .пере­менными Хи х2, …, хп применяют булево сложение—(дизъюнк­ция) И булево умножение (конъюнкция). •

При условии, что обе возможные реализации булевой, пере­менной фиксируются только числами 0 и 1, булево сложение и умножение можно заменить алгебраическими операциями. Опе­рации сложения И умножения В булевой алгебре ДЛЯ: — всех 2га реализаций булева вектора (хі, х2, хп) представлены в. табл. 1.2.

	Булевы переменные	11 Л X/ i=1 1
Номер операции	Л*1	-V2		■ ХП — 1	Хп	.11 V X/ i=1 1
0	1	1		1	1	1	1
1	1	1		0	1	1	0
2	1	1		1	0	1	0
2П—2	0	0		0	1	1	0
2П-—1	0	0		0	0	0	0

Из таблицы можно вывести следующие соотношения: п п Д xi = П Xi = min(xi………………….. Хп); i=l i=l

V xi = 1 — П (1 — л:і) = max(xi, хп).

і = і / = 1

Для краткости анализа бывает целесообразно при построе­нии моделей наряду с булевой переменной х рассматривать пе­ременную х, которая является отрицанием х. Переменная х оп­ределяется в той же области значений, что и х. Из принятого определения ясно, что реализации х и х не должны совпадать. Поскольку реализации булевых переменных есть числа 0 и 1, то А’=1—х. Для краткости в дальнейшем используем вектор­ную форму записи. Условимся, что х = {хх, х2, …, хп)т являет­ся булевым вектор-столбцом с п элементами. Здесь индекс Т означает операцию транспонирования. В частности, можно за­писать:

1_ = -(1, …, 1Д; 0= (0, …, ОД.

Наряду с функцией работоспособности S (х) =S(xі, …, хп) рассмотрим структурную функцию отказа S (х). Она определя­ется. любым из двух эквивалентных выражений:

S (х) = 1 — S (х), или S{x) = 1 — S (х).

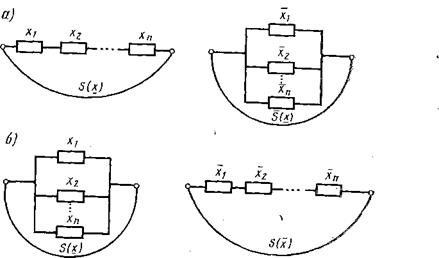
Сложные системы целесообразно разбивать на подсистемы, которые графически представляются в виде последовательного или параллельного соединения элементов. Структура, представ­ленная на рис. 1.3, а, применима к такому классу систем, кото­рые работоспособны только’ тогда, когда все п элементов ее работоспособны. Система отказывает, если отказывает хотя бы один из ее элементов. Для такой структуры можно записать 2* J9

1.3. Последовательное (а) и параллельное (б) соединение элементов

следующие аналитические выражения функций работоспособно­сти и отказа соответственно: ■

п

S(x) = Хп) = Л Xi =

*— < = і

71 _ П

= 1 — V = П Xi

І = 1 1 = 1

S(x) = max(^i, …. Xn) = V =

— t=i

n n

= 1 — Д я,- = 1 — П Xi.

i = i i — i

Структура, представленная на риє. 1.3,6, работоспособна* если работоспособен хотя бы один из ее п элементов. Система) отказывает только тогда, когда отказывают все п ее элементов. Эти условия запишем следующим образом:

71

S(a’) = max (at, …. Хп) = V Xt = — "

і = і

1 — П xt;

S(X) = ШІПІХЧ, …. Хп) = 1 — V Xi = П Xi.

— i=i <=i

Наиболее известные методы анализа надежности — это ме­тоды узлов и замкнутых контуров ![19]. Целесообразнее выбрать метод, при котором наименьший объем вычислений. Объем вы­числений можно сократить, объединив несколько компонент в. одну ветвь. Для метода узлов рекомендуется объединение ком­понент, расположенных последовательно друг за другом, а для метода контуров — параллельно.

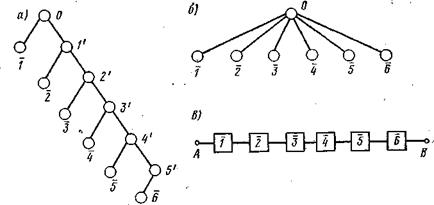
Деревья отказов. Они позволяют наглядно представить ха­рактер изменения надежности технической системы, восполь­зовавшись ориентированными графами со структурой в виде де­рева. Для такой структуры характерно наличие главного собы­тия 0, наступление которого соответствует отказу системы. При построении и анализе графа рассматривают причины появления события 0 и приходят к установлению событий, которые рас­сматриваются как основные и далее градации не подлежат.

Проанализируем работоспособность достаточно простой ава­рийной системы выпуска шасси на самолете Ил-86. Система со­стоит из ручного привода (рукоятки управления) и тросовой проводки, присоединенной к замкам убранного положения сто­ек шасси. Главное событие 0 заключается в отказе системы,, когда при ее использовании выпуск шасси не происходит. Дере­во отказов (рис. 1.4, а) для основных событий и упрощенное де­рево отказов (рис. 1.4,6) могут быть представлены как струк­турная схема надежности системы (рис. 1.4, в).

При помощи деревьев отказов можно переходить к рассмот­рению структурных схем надежности и далее отыскивать буле­вы функции работоспособности системы.

1.4. Дерева отказов системы аварийного выпуска шасси: О — шасси не выпускается: _/ — недостаточное усилие воздействия на (рукоятку; Ґ — рукоятка не перемещается; 2 — неправильное использование предохранительной защел— ки; 2′ ■— свободное перемещение рукоятки; 3 — обрыв тросса; з’ — заклинивание тросса; 4 — заклинивание — проводки; 4′ — заклинивание замка; 1— искривление (износ) рабочей.? поверхности замка; S’— попадание посторонних предметов; ЇГ—образование льда на рабочей поверхности замка

Для определения булевых функций с помощью деревьев от­казов можно использовать метод минимальных сечений и мини­мальных путей ][13, 19], основанный на анализе логических свят зей типа «И» и «ИЛИ», как наиболее простой.

Модели отказов с восстановлением. Модель, представленную в предыдущем подразделе, можно использовать в более общем случае’, если рассматривать отказы элементов как функцию вре­мени. Для невосстанавливаемых систем состояние ‘1-го элемен­та молено рассматривать как случайный процесс Xi(t), который •связан с наработкой Т* следующей зависимостью:

При восстановлении отказавшего У3-,*-го элемента требуется время на отыскание и устранение дефекта. В общем случае для процесса Xi(t), когда (1=1, 2, …, п), можно записать:

пг — 1 /71 — 1

Г 1, если 2 (Tt, і + Yj-i) <1< 2 (Ті, і + У/,,-) + Тт, ї, x(t) = /=‘ (1.39)

(0, в противном случае.

Графически реализацию случайного процесса ху(1), где ij, i и yj, i — реализации случайных величин Tj4 и У,,*, 1=1, 2, …, можно представить рис. 1.5. Если Tj, it j — 2, 3, … и Yj, it 1, 2,… являются независимыми случайными величинами, одинаково распределенными, то случайный процесс (1.39) образует аль­тернирующий процесс восстановления.

Для оценки надежности элементов восстановлением вместо вероятности безотказной работы 1-го элемента рассматривается такой показатель, как готовность 1-го элемента Vi(t). Он озна­чает, что 1-й элемент исправен в момент времени і. Обозначим через Hi(t) математическое ожидание числа циклов восстанов­ления 1-го элемента. Тогда

Vi(t) = Р(Ти >t) + Ri(t-x)dH,(x), о

где Ri(t — х) — вероятность того, что до момента времени t не было ни од­ного отказа 1-го элемента, а последний цикл восстановления закончился в мо­мент времени..V.

Если процесс восстановления при t-*-oо имеет стационарные отношения,’ т. е. «устанавливается», то

Если долю времени, в течение которого 1-й элемент внутри интервала (0, if) находится в состоянии отказа, обозначить че­рез ai(f), то математическое ожидание этой случайной величи­ны можно рассчитать, зная показатель готовности:

Е [<*,(/)] = / [l — Vi(x)]dx. о

В стационарных условиях

П. ц£М*)1 _! у_ E(Y)

г^°° t ‘ £(П)+£(Уг) ‘

Переходя от рассмотрения состояния элемента к состояниям системы по аналогии, получим [19]:

v.(f) =S[lM0, …. V„(*)];

У, = 1ітУ»(0 =S(Vi, …. V„);

£[М*)] = J [1 — Vs(x)]dx — о

Urn _

t s’

где ps(i) — доля времени, в течение которого система находится в исправ­ном состоянии.

Марковские модели. Они используются для систем, поведе­ние которых описывается случайным процессом Z(t) с конеч­ным множеством состояний М = (Zi, Z2, …. Zm). Процесс можно охарактеризовать маркированием точек [Si, Z(S* + 0)] для S0 = — 0<C-Si<S2<…, т. е. указанием точек скачков и состояний, в которые после этих скачков попадает система (рис. 1.6, а).

Если пренебречь временем пребывания процесса в определен­ном состоянии Si, то можно упростить исследование и рассматри­вать вложенную случайную последовательность {Z{, i=0, 1, 2, …} (рис. 1.6,6).

Если же учитывать не все маркированные точки/а лишь те, для которых Zi принадлежит только определенному (ограничен­ному) множеству состояний М, то получается вложенный про­цесс (Z(f), t>0} (рис. 1.6, в).

В теории вероятностей подробно рассматриваются случайные процессы, которые обладают так называемым свойством марко­вости: будущее поведение процесса не зависит от его прошлого, а определяется лишь его настоящим.

Отсюда следует, что в случае, когда настоящее представляет собой время после t-й (можно 1-й) смены состояния, свойство марковости можно выразить так [19]:

Р{ (Ь <t)A (Zi = Zi) Zo = Zi — 6i = U.. Zi-2 = zh — ■

b-i = U-uZi-i = z,} = P{(E, < 0Л (Zi = Zi) Zt-i = z,}, где /, k, …. / = 1, 2, …, m.

ra) nth >

X-

1 — І і

 

1.6. Реализация случайного процесса

Необходимо принимать во внимание требование однородно­сти, в соответствии с которым правая часть выражения не долж­на зависеть от числа шагов, т. е.

Р{Ь < fЛ (Z = Zj) I Z,_t = Z,} = Qj, i (t), где /, / = 1, 2, …, m, (=2, 3 … .

Для вероятностей P{Z(;t) = Zj} = Pj(t) пребывания процесса •в состояниях для любого момента времени t выполняется соотно­шение

Обозначим через Р, = 0 вероятности начальных состояний и введем для краткости вектор

Pit) = lpi(t), Ра it)………… Pm(t)]T

и матрицы

Q(t) = [<М*)]ы = 1, 2, …. т.

£(<) = [Qij(*)]/.«= 1. 2, …. т,

Тогда, задавая величины

{М, р^О), .(Д*), Q(f); f>0),

можно однозначно определить марковский процесс восстановле­ния. Если множество состояний М включает лишь два состояния (т = 2), то приходим к альтернирующему процессу восстановле­ния. Если матрицы Q (t) и Q (t) совпадают, а длительность пре­бывания gjпроцесса в определенном состоянии не рассматри­вается, то марковская цепь однородна.

Такая марковская цепь характеризуется величинами

{М,_р(0), Р_ = (Ры)}.

Если свойство марковости процесса выполняется лишь для подмножествам состояний системы, тогда соответствующий вло­женный случайный процесс {Z(t), 0} называется полумарков-

ским. Для обоснованного применения полумарковских моделей необходимы предварительные исследования, состоящие из двух этапов. На первом этапе определяют состояние системы и вы­являют временные характеристики, соответствующие процессам восстановления. На втором этапе оценивают моменты переходов: (вложенная цепь) и выявляется наличие марковских свойств. ■ Указанные условия констатируют факт полумарковости процес­са и возможность использования полумарковских моделей.

На практике часто возникает необходимость распространить; структуру процесса переходов (матрицу частот переходов) ло­кальной системы на совокупность однотипных систем. Для это­го требуется доказать эргодичность процесса на определенном; отрезке времени.

Стохастический процесс называется стационарным, если его: вероятностные характеристики (математическое ожидание, дис­персия, корреляционные моменты) не зависят от момента вре­мени, в котором рассматривается этот процесс [19]. Стохастиче­ский процесс называется эргодическим, когда с вероятностью 1 среднее по времени равно среднему по реализации [23]. Ста­ционарный процесс считается эргодическим, если нормирован­ная корреляционная функция стремится к нулю при условии, что и рассматриваемое приращение времени также стремится к’нулю [19, 23].

Применение полумарковских моделей будет рассмотрено в § 3.2 и 3.3 при решении прикладных задач оценки и оптимиза­ции программ ТО и Р.

Границы применения булевых и марковских моделей надеж­ности. Использование булевых ‘моделей обусловлено необходи­мостью рассмотрения лишь двух состояний элементов систе­мы, а именно состояний отказа и работоспособности.

Структурная схема надежности позволяет выявить несколь­ко возможных реализаций отказов. Но при этом исчезает свой­ство независимости функционирования элемента относительно всех видов своих отказов. Это один недостаток. Другой заклю­чается в том, что условие монотонности не всегда выполнимо.

Последовательность, в которой отказывают отдельные ком­поненты системы, играет существенную роль. Невозможность учета временной последовательности отказов элементов также является недостатком булевой модели. Характер отказов от­дельных компонентов системы часто зависит от состояния дру­гих компонентов, что не учитывается в булевых моделях, так как в них предполагается независимость компонентов.

Теперь рассмотрим недостатки марковских и полумарков — ских моделей. Анализ надежности с использованием марковской модели возможен в том случае, если интенсивности переходов между отдельными состояниями системы являются постоянны­ми величинами. Если интенсивности переходов зависят от вре­мени, то расчеты неоправданно усложняются. Если отдельные интенсивности не известны, то нельзя составить необходимую систему дифференциальных уравнений с зависимыми от време­ни коэффициентами.

Использование марковской цепи, вложенной в случайный процесс, расширяет возможности использования марковских моделей надежности. Но для однозначного описания марковской цепи необходимо знать число возможных состояний, вектор рас­пределения начальных вероятностей и матрицу вероятности пе­реходов. На практике удобно пользоваться графом состояний и переходов, разметку ребер и вершин производить с помощью матрицы вероятности переходов и вектор-строки стационарных вероятностей. При этом следует убедиться, что поглощающие состояния отсутствуют. А это требует доказательства стацио­нарности и эргодичности процесса (вложенной цепи).

При использовании полумарковских моделей должны выпол­няться следующие условия:

матрица частот переходов удовлетворяет условиям стохас­тической или марковской матрицы;

частоты переходов для каждого из состояний зависят от этих состояний и не зависят от более ранних состояний;

вектор абсолютных частот попадания системы в каждое из состояний имеет только стационарные составляющие;

случайные величины времени пребывания системы в раз­личных состояниях имеют функции распределения;

процесс переходов является стационарным и эргодическим на рассматриваемом отрезке времени.