ПОКАЗАТЕЛИ ПАРАМЕТРИЧЕСКОЙ БЕЗОТКАЗНОСТИ НЕВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА

При рассмотрении показателей безотказ­ности невосстанавливаемого элемента, работающего непрерывно от момента включения до первого отказа, оперируют случайным време­нем т возникновения отказа или жизни элемента. Для любого элемента может быть установлен вектор параметров состояний;

х(/)-{X,(0, х2(0,, х,(t),…,xh(0>,

зависящий от времени I, а также векторы, ограничивающие допусти­мые пределы изменений X(t) снизу:

*h(‘) = {*hi(0, х„.(0. …. xHi(/),…, xuh(t)}

н сверху:

*в (0 — <*в, (0. *в2 (0. -. *ві (0……………….. *в* (*)}•

При этом выход любого параметра Хг(0 за соответствующие пределы АXBi(t) должен рассматриваться как отказ элемента. Такая постановка отличается от рассмотренной в § 2.2 тем, что имеется более ілубокое представление о процессе функционирования элемента и есть возможность контролировать или прогнозировать изменение парамет­ров X(t). В этом случае можно говорить о параметрической безотказ­но, та элемента, которую численно также характеризуют вероятностью безотказной работы элемента за заданное время. За время t в парамет­рической постановке вероятность безотказной работы элемента

дп(0 = вер(т > о = вер(Хн(0< Х(0< Хв(0). (2.26)

Из-за отклонений свойств элементов, условий и режимов их эксплу­атации все параметры X(t) в общем случае можно рассматривать как случайные функции. Допустимые пределы Xu(t) и XB(t), если они заданы в эксплуатационной документации, являются детерминирован­ными (неслучайными) функциями. Однако часто и пределы можно рассматривать как случайные функции, так как весьма сложно найти в каждый момент t такое точное значение, например, Xui, что при ве­личине параметра X; = Х„г i~dXui элемент работоспособен, а при Хі = Хні — неработоспособен.

Таким образом, состояние элемента описывается вектором случай­ных функций, причем все функции в этом векторе зависимы или хотя бы коррелированы (имеют случайную линейную зависимость), так как отражают работу одного и того же элемента. Вектор случайных функций характеризует состояние достаточно большой группы одно­типных элементов. При работе одного элемента этот вектор случайных функций представлен случайными реализациями Xi(t), x2(t), …, хг(0.

…, xh(t) параметров. Аналогично обстоит дело и с векторами случай­ных функций XH(t), XB(f).

С учетом этого в самом общем случае задача расчета параметри­ческой безотказности состоит в отыскании вероятности того, что за время t ни одна из реализаций xt(t) случайных функций Xt(t) не выйдет за реализации xEi(t), xBi(t) случайных функций XHi(f), XBt{t). Для решения такой задачи необходимо знать законы совместного рас­пределения функций Xt(f), Xm(t), XBi(t) в каждый момент времени t; при этом расчет сводится к громоздким вычислениям многомерных интегралов. Поэтому в такой постановке без упрощающих допущений задачу практически не решают. Если предположить, что функции XHi(f) и XBi(t) неслучайны и детерминирование определяют область D(t) работоспособных состояний элементов для всех t, то в этом случае

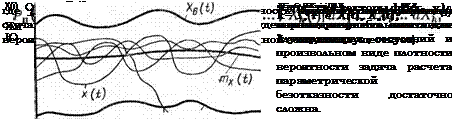
ций, а функции, показан на рис. 2.4. Неслучайные функции Xu(t), XB(t) образуют поле работоспособных состояний. Случайный процесс X(t) представлен математическим ожиданием mx(f) и реализациями х((), одна из которых вышла за нижний предел (момент т отказа элемента).

Достаточно просто решаются задачи, когда необходимо определить вероятность Q(l) выхода (выброса) реализации одной случайной функ­ции X(t) на интервале (0, t) за постоянные уровни Х„, Хв. Если считать независимыми событиями выбросы X(t) за уровни Хп и Хв, то можно свести задачу к опреде­лению вероятностей QM и Q„(f) выброса случайной функции X(t) за один (нижний А’н или верхний Хв) уровень. Естественно, в силу принятой независимости событий

<2(0 ~ <2н(0 + QM — (2.28)

Используя результаты, приве — Рис. 2.5. Положительный выброс денные в [571, рассмотрим воз — реализации случайной функции за

постоянный уровень

можности вычисления вероятности QJJ) пересечения реализацией слу­чайной функции X(t) уровня Хв снизу вверх. Такой выброс назы­вают положительным, а при пересечении уровня сверху вниз — отрицательным.

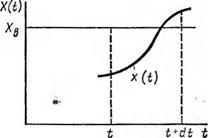
Выберем такой малый интервал времени dt, на котором может быть только один положительный выброс (рис. 2.5). Он может произойти, если X(()■<. Хв и X(t + dt)> Хв. Будем полагать, что X(t) — диф­ференцируемая случайная функция, и введем V{t) = —fjp——————————————————————————————————- слу­

чайную функцию скорости изменения случайной функции X(t). Тогда условие положительного выброса X(t) за Хв на интервале dt можно записать в виде X(t)<. Хв и X(t) + V(t)dt > Хв, или

Хв — V(t)dt< X(t)< Хв, V(t)> 0. (2.29)

С учетом этого на интервале dt элементарная вероятность поло­жительного выброса

dQB(t) = вер[Хв — V(t)dt< X(t)< Хв]. (2.30)

Для вычисления этой вероятности необходимо знать закон совме­стного распределения случайных функций X(t) и V(t) в каждый про — н шольный момент t. Пусть задана плотность f(x, v/t), тогда для опре — леления вероятности (2.30) необходимо проинтегрировать эту ПЛОТ­НИШЬ по х от Хв — vdi до Хв, а затем, чтобы перебрать все возможные шнчения и скорости процесса, по v от 0 до сю, так как по условию за­дачи 1/(0> 0. Таким образом, получим

dQB( 0 = J j f(x, v/t)dxdv. (2.31)

0 Xg—vdt

Внутренний интеграл может быть легко взят при использовании теоремы о среднем значении, так как пределы интегрирования отли­чаются на бесконечно малую величину

J / (х, v/t) dx = (Хв — Хв + vdt) f (Хв, v/t) = vdtf (XB, v/t). (2.32)

X~vdt

Подставляя (2.32) в (2.31), получим

сю

dQB (t) = dt f / (XB, v/t) vdv. (2.33)

6

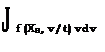Таким образом, на интервале dt вероятность выброса случайной функции за уровень пропорциональна величине интервала, а вероят­ность выброса функции в единицу времени

Для определения вероятности выброса функции за нижний уро­вень Хп составим неравенство типа (2.29). Для того чтобы на интер­вале (t, t -j — dt) произошел выброс за нижний уровень Хн, необходимо выполнение условий X(t)> Х„ и X(t)—V(t)dt<iXH, где V(t)> О, а направление изменения X(t) учтено знаком перед V(t)dt. Тогда по аналогии с (2.30)—(2.34) получаем

dQH (t) = вер (Хн < X (t) < Хн + У (0 dt] =

ОО сю

— f j f(x, v/t) dxdv — dt^f (X,„ v/t) vdv, 0 xH 6

oo

d^ = j/(*H. V/t) vdv.

Вероятность выброса случайной функции X(t) в единицу времени за верхний или нижний уровень при допущении о их независимости определяется очевидным выражением типа (2.28):

dQ(t) dQB(t) , dQ„(t)

——— г»———— -+- ———- .

dt dt dt

Тогда вероятность выброса на интервале (0, 0 с учетом (2.34) —

(2.37) принимает вид

Наконец, за время t вероятность безотказной работы элемента PD(t) = 1 — Q(t) = 1 — J jj f(XB, v/t) +f(X„, vlt)]vdvj dt. (2.39)

Представляет интерес частный случай, когда безотказность эле­мента высока и поток выбросов можно принять пуассоновским.

В этих условиях случайное число отказов на произвольном интер­вале (0, t) будет подчиняться закону Пуассона (2.1) (см. табл. П.1). Для этого закона найдем вероятность Рв0 того, что на интервале (О, t) не будет ни одного положительного выброса. В соответствии с (2.1) для случая т = О

PUt) = е—‘(О, (2.40)

где a(t) — математическое ожидание числа положительных выбросов за время (0, t).

Используя (2.34) для вероятности положительного выброса в еди­ницу времени, получим

Аналогично, с учетом (2.36), (2.41), (2.42) вероятность отрицатель­ных выбросов

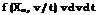
(2.43)

Если положительные и отрицательные выбросы независимы, то на интервале (0, t) вероятность не получить ни одного положительного и отрицательного выброса

Pott) = Pn(t) = Pu0(t)PUt). (2-44)

Подставим (2.42) и (2.43) в (2.44). После элементарных преобра­зований получим

Рп (t) = exp j j — j JJ If (XB, vlt) + f (X„, v/t)] otfoj d/JJ. (2.45)

Заметим, что при использовании закона Пуассона предполагают

величину Pu(i) близкой к единице. В этих условиях выражения (2.39) и (2.45) практически совпадают [см. (2.23) и табл. 2.1].

Для практики важен случай, когда процесс X(t) — стационарный. Как известно из [53], [57], различают стационарный случайный про­цесс в широком и узком смысле. Стационарность в широком смысле (менее точно, чем в узком смысле) выполняется, если для веществен­ной случайной функции X(t):

1) ее корреляционная (автокорреляционная) функция

KJtu h) = ЛГ{[ВД — /л*Р,)][ВД — (2.46)

зависит не от моментов времени tlt tz, а только от их разности т = — tz — 11, т. е.

К At и h) = /С(т); (2.47)

2) математическое ожидание случайного процесса постоянно, т. е.

mx{t) = тх = const; (2.48)

3) дисперсия процесса постоянна, т. е.

D [X (/)] = ol(t) = о2х= const. (2.49)

Для стационарных дифференцируемых процессов характерны кор­реляционные функции вида (см. [57])

КХ(А = о2 е~“!тЄ; Кх(т) = о2 ё~а‘%2 cos рт; Кх(т) = о2хе a|4^cosPx — f-j-sinp I Т I );

/Сх(т) = оІе-,т|(1+«|т|).

где а, р — постоянные параметры.

Для т = t2 — t = 0 имеем

КМ = D(X(t)] = DX = ol.

Заметим также, что в инженерных задачах при невыполнении тре­бования стационарности (2.48) можно рассматривать центрированный случайный процесс

Y(t) = X(t) — mx(t) (2.52)

с математическим ожиданием my(t) — 0.

Таким образом, существенным, а в практических задачах часто и достаточным признаком стационарности случайного процесса являет­ся выполнение условия (2.47).

Для стационарного (в узком смысле) случайного процесса плот­ность вероятности f{x/i) и плотность вероятности f(x, v/t) не зависят от времени, т. е. имеют вид f(x), f(x, v). С учетом этих соображений вероятность отсутствия положительных выбросов случайной функции X(i) на интервале (0, /) в соответствии с (2.42) для стационарного про­цесса

Яво (0 = exp |^-1 Jf (XB, V) vdv1, (2.53)

аналогично, выражение (2.43) принимает вид

Яно (‘) = ехр Г— f J /(Хи, v) vdvj. (2.54)

В соответствии с (2.44), (2.53),(2.54) вероятность отсутствия выбро­сов за нижний и верхний уровни в течение времени t для стационар­ного случайного процесса Х(1) определяется выражением

Яп (0 = ехр {-1 j [f (Ха, v) + / (XHf v)] vdvJ. (2.55)

*•

Для наиболее распространенного в практике и изученного в тео­рии случая, когда стационарный процесс имеет нормальное распре­деление, двумерная плотность вероятности f(x, v) самого процесса X(t) и его скорости V(i) распадается на произведение нормальных плотностей f(x) и f(v), так как в каждый момент времени t случайные величины X и V в силу нормальности распределения становятся неза­висимыми (см. [57]). Следовательно, для нормального стационарного процесса

/<*, ») = /<*>№)- —!=. ^. (2.56)

ах у2п a. v У 2т

( XD — mxfl (2^) 1 — v*/(2^)

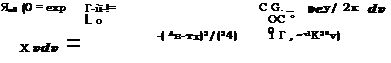В силу стационарности случайного процесса X(t) mx(t) — tnx — const, a mv = 0. Подставляя (2.56) при x = Хв в (2.53), получим

Интеграл в (2.57) является табличным (см. Г26І) и равен ої;. С уче­том этого

Известно, что для стационарного дифференцируемого процесса

(/) существует вторая производная корреляционной функции —

чсрез которую выражается дисперсия скорости этого процесса (см. 1571):

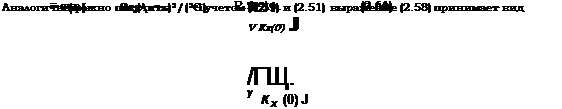(2.59)

В соответствии с (2.44), (2.60) и (2.61) вероятность отсутствия вы­броса случайной стационарной нормальной функции за нижний или верхний предел в течение времени t будет

— ( Хв~тх )2//(2з*)

е +

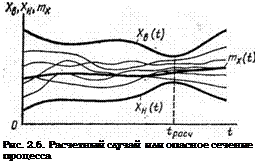Дальнейшее упрощение задачи расчега параметрической безотказ­ности элемента может быть получено, если на интервале (0, t) для слу­чайного процесса X(i) най­дено опасное или расчет­ное сечение А>асч, в кото­ром вероятность возникно­вения параметрического отказа больше, чем в дру­гие моменты времени. Это может быть связано с тем, что в сечении /Расч боль­ше дисперсия процесса

^л(Ансч) — 0 (^Расч) ИЛИ

ближе к математическому ожиданию mx(tPac4) лежат допустимые пределы

•^о(А>асч)> -^н(^Расч) изме­нения функции X(t) (рис. 2.6). Если удается найти такое сечение процесса, то рассматривают задачу о вероятности Рп(/Расч) = Рп вы­хода случайной величины X(tv&c4) — X за пределы А’н(<Расч) = А,„

■^в(^Расч) = Ав.

Ри = вер(Х„< А< Хв).

Найденную таким путем вероятность Р„ принимают за вероятность того, что на всем интервале (0, t) случайный процесс X(t) не выйдет за пределы XR(t), XB(t). Такое допущение достаточно сильно, но в
инженерной практике широко применяется. Так, при расчете кон­струкций ЛА и других составных частей ЛК находят такой расчет­ный случай функционирования, при котором действующие нагрузки максимальны. Например, прочность хвостового отсека ЛА обычно рас­считывают для случая вертикального расположения аппарата на стар­товом устройстве или передачи через него в полете на корпус макси­мального тягового усилия от двигателя; прочность болтов, крепящих отдельные отсеки корпуса ЛА, рассчитывают на усилия при пере­грузке ЛА и на нагрузки в полете в некоторых точках траектории.

Рис. 2.7. Определение вероятности параметрического отказа элемента

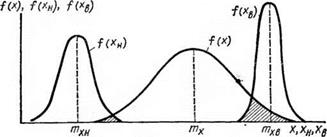
При описании состояния элемента случайным процессом X(t) практически не удается учесть возможные случайные изменения пределов Х„, Хв, выход за которые ведет к параметрическому отказу. I ели же состояние элемента определяется только одним случайным параметром X, то нетрудно учесть и переменность пределов. При этом задача сводится к тому, чтобы вычислить вероятность (2.63), если заданы функции распределения случайных величин X, Хн, Хв. На рис. 2.7 дана графическая интерпретация задачи для случая, когда эти вели­чины непрерывны и заданы плотностями вероятностей f(x), fH(x„), /’„(а’„). Далее для простоты изложения символом f обозначены различ­ные плотности вероятности. Заштрихованные площади соответствуют вероятности параметрического отказа, при котором реализованные значения х, х„, хв случайных величин X, Х„, Хв таковы, что х<. х„ или х> ха. Для вычисления вероятности параметрической безотказ­ности введем случайные величины:

FH = X — Хи, (2.64)

= Хв — X. (2.65)

Тогда вероятность Рп того, что случайная величина X не выйдет за случайные уровни Хн, Хв, может быть вычислена как

Рп = вер (К„> 0 и Гв> 0). (2.66)

Случайные величины Yn и Yв зависимы, так как в них входит одна н та же случайная величина X. Поэтому для вычисления вероятности

Рп необходимо знать совместную плотность вероятности f(yH, ув). Если такая плотность найдена, то вероятность одновременного попа­дания случайных величин Ен и YB на интервал (0, оо) определяется выражением

оо оо

Ра = J |* / {Ун> Уві) dyHdyB. (2.67)

о 6

Если опасен выход случайного параметра X только за какой-либо один предел Хи или Хв, то задача существенно упрощается, так как приходится оперировать с одной случайной величиной YH или Ев. При этом

Ра = веР (Yа > 0) = J7 (Ун) dyH о

оо

Рп = вер (Ев > 0) = J / (ув) dyB.

Для определения плотностей f(yu), f(yD) и f(y„, ув) необходимо знать исходные плотности вероятностей f(x), f(xH), f(xB) случайных величин

X, хн, хв.

Закон распределения случайной величины Y„ (2.64) может быть найден, если известна плотность вероятности f(x, хн). Функция рас­пределения F(y„) случайной величины Yn может быть записана в виде

вер (Y„ с ун) = вер (X — Хн< у„) = F (ун) = f j f (х, хи) dxdx„, (2.70)

<D)

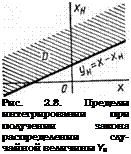где D — область интегрирования, определяе­мая выражением (2.64).

На рис. 2.8 область интегрирования D, для которой выполняется условие х — х„< t/н, за­штрихована. С учетом этого выражение (2.70) можно записать следующим образом:

ОО ОО

F (ун) = j j f{x, xa)dxdxH

-°°*h

to Г оо "I

= I j f(x, xH)dxadx.

— со _x—y J

Дифференцируя (2.71) no переменному нижнему пределу внутрен­него интеграла, найдем плотность вероятности:

— со _ X—V -*

СО

= J f(x, x — yH) dx.

—оо

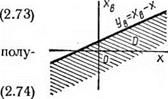
Аналогично можно получить плотность вероятности случайной величины YB, если известна плотность f(xB, х). На рис. 2.9 показана область интегрирования D. В соответствии с этим имеем

х+ув

F (ув) = j j f(xB1x)dxBdx,

чим

f{yB) = J f(x+yB, x)dx.

ж Рис. 2.9. Пределы ин — Если случайные величины X и Хн или Хв*и тегрирования при по-

X независимы, то совместные плотности вероят — лучении законарас — . і, пределения случайной:

постен f(x, хн) или Дхв, X) разделяются на про — v величины Ув

взведение плотностей отдельных случайных ве­личин:

f(x, Хп) = f{x)f(xBy, f(xB, х) = f(xB)f(x). (2.75)

При этом выражения (2.72) и (2.74) упрощаются:

/Ы= ] f(x)f(x-yjdx; f(yB)= j f(x+yB)[{x)dx. (2.76)

—оо —со

/(*) = f(X„) f(XB)

Если случайные величины X и Х„, Хс и X независимы и имеют нор­мальное распределение с плотностями вероятностей

то плотности вероятностей случайных величин и FB могут быть легка вычислены.

В соответствии с (2.75) и (2.77) имеем

“ — (x~mxf /(2^) _ ( хи-тх)2/(2*| ) J е *•

 

После преобразования подынтегрального выражения и вычисле­ния интеграла получим

— [ ув — ("V-m )]2/[2 ( 4 + 4Н )1

———— =е

(2.78)

•у = иг* — m, ; ov іЛт* + a* .

ад т„в = — т*, = |/ ^ + о* .

Таким образом, случайные величины Кн и имеют в рассматрива — мом случае нормальные распределения с характеристиками, определяе­мыми выражениями (2.78) и (2.79). Для определения плотности /(у,,, т/в) необходимо учесть зависимость нормально распределенных вели­чин Кн и FB. Искомая плотность /(ун, у„) будет тоже нормальной, но. с другими параметрами:

2р(Ун-ту„)(ув-т>.в) (Ув-тУв)2

Ув

ад т. у — тх т ; т„ = тх —тх о„ = |/ с4 + с4; о;/ =

и___ нив н и в

1 / 2 2

= (/ Охв-{-ох; р — коэффициент корреляции случайных величин Г„ и Кв.

Для определения значения р найдем сначала корреляционный мо­мент:

К — М [(Уя my^{YB — Ха — тх +

+ mx^j (*, X тжв + mx)j. (2.81)

Перемножим члены в скобках под знаком математического ожида­ния:

К = М [ХХВ — ХНХВ ~тхХв + тхХв — Х*+ Х„Х + тхХ —

— тхХ — ХтХв + ХнтХа + пгхтХв — тхт ^ + Хтх ■ — Хитх — ті + тХптх].

+ "**"4 — М [X2] + т тх +

Математическое ожидание суммы случайных величин равно сумме математических ожиданий, и математическое ожидание произведения независимых случайных величин равно произведению их математи­ческих ожиданий, поэтому

-f т2 — тх тх — Шуіпх + тх тх + тхтх — тхтх +

+ ті — тхтх — mi ф — тхтх.

После приведения подобных членов и с учетом того, что ai = = М [X2] — т2х, окончательно получим

К = —ol (2.82)

Поскольку ai > 0, то корреляционный момент для случайных величин Ун и Yв — отрицательный. Это можно доказать и логически­ми соображениями. Чем меньше значение у„ случайной величины Y„, т. е. чем ближе значение параметра х к нижнему пределу х„, тем в среднем больше значение ув случайной величины К„, т. е. тем дальше отстоит значение х от верхнего предела хв.

С учетом (2.80), (2.82) коэффициент корреляции

р = XI(oyOyJ = — о2/ }/К+аУК0 + аІ) ■ (2-83)

Полученные выражения для плотностей вероятностей f(y„, ув), 1′(уи), f(yB) позволяют найти и искомую вероятность отсутствия па­раметрического отказа. Когда случайный параметр X не должен выйти за нижний Х„ и верхний ХБ случайные пределы, при допущении о независимости величин X, Хн, Хв и нормальности их распределения в соответствии с (2.67) и (2.80) имеем

Интеграл (2.84) может быть вычислен с использованием таблиц для двумерного нормального распределения в виде

Ри ■ 0,бФ0(оСц) I 0,5Ф0(ав) — Т(а„, рн) Т(ав, рв),

где

[«н = m«JaU„ • ав = тУв1°Ув ;

Рн = (“в—анР)/(“„ V I — Р2) ; Рв= (ан— авР)/(ав Vl — р2) . I

Таблицы значений функций

Ф0(*) — —у=г Г е~< /2 dt;

У 2r. J

—— 00

~Т ^

е ——-

1 + Х2 О

^представлены в работах [48, 59]. Таблицы интегралов Т(а, р) доста­точно громоздки. Заметим, что для случая р = О необходимость в них отпадает. В этом случае при нормальном законе распределения условие некоррелированности случайных величин К„ и Ув обеспечи­вает и ИХ независимость, Т. е. ПЛОТНОСТЬ вероятности f(yн, ув) = = }(yH)f(yB)- Тогда в соответствии с (2.84) получим

(2.88)

. п -/*/2

Значения функции (2.86) Ф0(х) =——- е dt приведены

V 2-к J

— 00

в табл. П. З.

Таким образом, после вычисления значения р по (2.83) можно оце­нить необходимость использования таблиц функции (2.87) для расчета параметрической надежности. В том случае, когда величина р суще­ственна, чтобы избежать использования громоздких таблиц, можно разложить систему двух случайных нормально распределенных кор­релированных величин YK, YB на две нормально распределенные не­коррелированные, а следовательно, независимые величины YH, YB со следующими параметрами (см. [12]): математическими ожиданиями

средними квадратическими отклонениями

о’2 == О2 COS2 а 4- /С sin 2а + ^ Sill2 а; уп Уп У в (2.90)

Ц = а sin2 а — д sin 2а + а„ cos2 а,

J/b J/н »в )

где К = —Ох — корреляционный момент случайных величин FH и YB [см. (2.82)|.

Параметр а является корнем уравнения

lg 2, = 2К / (- .Ц — — К/ ( V — «JJ • <«1)

В (2.91) предполагается, что оу^> оУв и угол а лежит в I квадран­те при р> 0 или в IV квадранте при р<; 0. Для случая, когда ауи =

Оув и ох> 0 (р< 0), искомый угол а = —45° и лежит в IV квад­ранте, а если оуп — оув и р> 0, то а = 45° и лежит в I квадранте.

Таким образом, при нормальном распределении параметра элемен­та и случайных нормально распределенных пределах, выход за которые рассматривается как отказ, задача расчета параметрической безот­казности при допущении о независимости перечисленных величин решается легко с использованием табличной функции (2.86). С учетом выражений (2.88) — (2.91) в этом случае имеем

Если недопустим выход случайного параметра X за какой-нибудь один (нижний или верхний) случайный предел, то вероятность пара­метрической безотказности с учетом (2.64) и (2.65) определяется выражениями (2.68) или (2.69).

В общем случае при заданных плотностях вероятностей f(x) и [(Хн) или /(хв) плотности f(yH) или f(yB) могут быть найдены по зави­симостям (2.72) или (2.74). Если случайные величины X, Х„(ХВ) не­зависимы, то f(yn) или f(yB) определяются выражениями (2.76). Нако­нец, при независимости и нормальности распределений этих величин плотности f(yH), f(yB) будут нормальными 1(2.78) и (2.79)1, а вычисление интегралов (2.68), (2.69) сведется к нахождению табличных значений функции (2.86):

Рп = вер (Г„ > 0) = вер (0 < YH < оо) =

Аналогично получим

•Рп = вер(Ев> 0) = Ф0(т^в|а^в). (2.94)

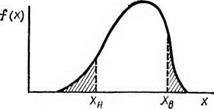
ри= f(*)dx. К На рисунке площади, определяющие вероятность параметриче­ского отказа элемента, заштрихованы. Даже для произвольного зако­на распределения вычисление интеграла (2.95) обычно не пред­ставляет труда. Если же слу­чайный параметр X имеет нор­мальное распределение с плот­ностью f/ ч і -(*-и*)7(*£) /(*) =———- —е V2*

Если пределы Хв, ХБ допустимого изменения параметра X явля­ются неслучайными, то задача (2.63) становится элементарной. Для ее решения нужно только знать плотность вероятности f(x). Если она известна (рис. 2.10), то

(2.95)

вероятность (2.95) при плотности f(x), заданной в форме (2.96) опре­деляется зависимостью

Ри = вер (Хн< X<Хв) = | f(X) dx = — (х-тху/(2і) /х — гг /тх — X е dx = Ф0 (-Д—aJ + Ф„( ж-о J — 1. (2.98)

Если необходимо в этих же условиях рассчитать вероятность вы­хода случайной величины только за верхний Хв или нижний Х„ пре­дел, то

Хв Ри = вер(X<Хв) = j /(x)dx=a>0

(2.99)

Рп = вер (Хн < X) = J f(x) dx = Ф0 Хн

(2.100)

Таким образом, задача расчета вероятности безотказной работы элемента за время t в параметрической постановке отличается от по­добной задачи, рассмотренной в предыдущем параграфе, тем, что здесь необходимы более глубокие сведения о процессе работы элемента. Действительно, для расчета вероятности безотказной работы по (2.14) необходимо знать только интенсивность отказов элемента k(f). Для расчета вероятности безотказной работы элемента в параметрической постановке были рассмотрены следующие задачи:

1. Состояния элемента определены векторами случайных функций (1), границы пространства работоспособных состояний также опи­саны векторами случайных функций XH(t), XB(t). Задача в общем виде практически неразрешима.

2.Состояния элемента определены вектором случайных функций X(t), границы пространства работоспособных состояний заданы век — горами детерминированных функций Хн(£), XB(t). Задача практически разрешима [зависимость (2.27)], если известен^ совместный закон рас­пределения вектора случайных функций в каждый момент времени t.

11ри большой размерности вектора X(t) и произвольном законе распре­деления необходимы громоздкие вычисления сложных многократных интегралов.

3.Состояние элемента определено одной случайной дифференци­руемой функцией X(i), границы области работоспособных состояний заданы постоянными величинами Хн, Хв. Задача довольно просто решается в общем виде [зависимость (2.39)1, если известен закон сов­местного распределения функции Х(() и ее скорости V(t) в каждый момент t [плотность f(x, vlt)]. Для стационарного случайного процес­са достаточно знать плотность вероятности f(x, v), при этом вычисле­ния упрощаются [зависимость (2.55)]. Если стационарный процесс имеет нормальный закон распределения, то искомая вероятность на­ходится по конечной формуле (2.62) при известных математическом ожидании и корреляционной функции процесса.

4. Состояние элемента задано случайной величиной X, а интервал работоспособных состояний — случайными пределами Хн, Хв в наи­более опасном (расчетном) сечении процесса функционирования.

Для решения задачи необходимо знать совместную плотность ве­роятности Ну„, ув) случайных величин YB — X — Хни7в = Хв — X 1см. (2.67)]. Если случайные величины X, Х„, Хв независимы и рас­пределены нормально, то вероятность параметрической безотказности находится с использованием таблиц по зависимости (2.92). Если не­допустим выход параметра X только за какой-нибудь один случай­ный предел, то при независимости и нормальности распределения слу­чайных величин X и ХН(ХВ) вероятность Р„ определяется по (2.93) или (2.94).

5. Состояние элемента задано случайной величиной X, а интервал работоспособных состояний — неслучайными пределами Х„ и Хв. В этом случае вероятность параметрической безотказности определя­ется интегралом (2.95). Если параметр X имеет нормальное распре­деление, то вероятность Рп находят через значение табличной функ­ции по (2.98). Если отказ наступает только при выходе нормально
распределенной величины X за один нижний (верхний) предел, то используют зависимости (2.99) и (2.100).

Проиллюстрируем возможности расчета вероятности параметри­ческой безотказности примерами.

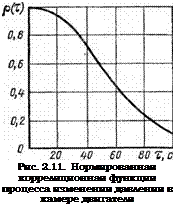
Пример 2.1. Пусть случайный процесс p(t) изменения давления в камере сгорания твердотопливного двигателя ЛА является стационарным нормальным с постоянными математическим ожиданием тр = 5МПа и дисперсией ар = = 0,0625 МПа2, а его корреляционная функция имеет вид Кр(т) = а2ре—а***,

где а = 0,015 с-1. Пусть также установлены неслучайные пределы: верхний рв = 6 МПа и нижний рп = 4 МПа, выход за которые расссматривается как параметрический отказ двигателя. Найти вероятность того, что в те­чение t = 100 с работы двигателя не про­изойдет ни одного выброса давления за уровни Рв> Рн> если выбросы за нижний и верхний уровни можно считать независимыми собы­тиями.

Прежде чем приступить к решению зада­чи, проанализируем случайный процесс p(t). На рис. 2.11 представлена нормированная корреляционная функция р(т) = Кр(т)/ар2. Анализ этого графика показывает, что слу­чайные отклонения давления, происшедшие в произвольный момент времени, в среднем до­статочно долго не затухают. Даже через т = = 100 с работы отклонение, возникшее в на­чальный момент, будет еще заметно сказы­ваться на отклонениях в сечении t = 100 с, так как р (100) « 0,1.

Реализации подобного процесса обычно достаточно гладкие функции, без резких колебаний. Если бы параметр а был значительно меньше, то влияние отклонений процесса в данный момент на отклонения через интервал т было бы слабее, а реализации процесса часто пересекали бы математическое ожидание и были бы менее гладкими. Наконец, при а = 0 случайный процесс p(t) можно рассматривать как нормально распределенную случайную величину р с парамет­рами тр и ор, так как взаимное влияние отклонений в различных сечениях про­цесса отсутствует.

Для определения по (2.62) искомой вероятности того, что за 100 с работы двигателя не произойдет параметрического отказа, необходимо найти вторую производную от корреляционной функции:

кР (*) = ;

. dKp (т) 2 _а!_2

Кр (т) ="" сТх—= — 2a2ve

d2Kp(t) 2 —u2t! 2 — „!,г

Кр (т) =——- ——— = — 2а2а^ е + 4-А^е

При т = 0 значения этих функций упрощаются:

Кр (0) = чр ; кр(0) —— 2а2зр.

С учетом этого по (2.62) найдем вероятность того, что в течение t — 100 с работы двигателя давление в камере не выйдет за пределы рн и рв:

 

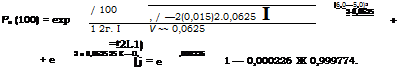Пример 2.2. Рассчитать вероятность параметрической безотказности твер­дотопливного двигателя ЛА в предположении, что его работоспособное состоя­ние определяется одним параметром — давлением в камере р. Давление имеет нормальное распределение с характеристиками тр = 5 МПа, с2 = 0,0625 МПа2, причем выход параметра р за неслучайные пределы ра = 4 МПа и рв — 6 МПа рассматривается как параметрический отказ.

Эта задача отличается от предыдущей тем, что вместо выхода случайного стационарного процесса за постоянные пределы рассматривается выход случай­ной величины за те же пределы. При этом, естественно, не учитывается длитель­ность процесса.

В соответствии с условиями используем для расчета вероятности Рп зави­симость (2.98) и табл. П. З: „

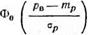рсв, -(^тр)2′(2І)

Ри = вер (Рн < Р < Рв) = I ————— —— е dp

J а„ у 2".

Рн

5,0 —4,0 0,25
4-Ф0	— 1 = Ф0
4- Ф„

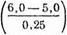
= Ф0 (4) 4- Ф0 (4) — 1 = 0,99996833 4- 0,99996833 — 1 як 0,999937.

Полученный результат из-за неучета продолжительности процесса превы­шает значение вероятности параметрической безотказности, полученное в пре­дыдущем примере (Рп — 0,999774).

Пример2.3. В условиях примера 2.2, но при рн = 4,25МПа и ра =5,75МПа, рассчитать вероятность параметрической безотказности двигателя.

Используя зависимость (2.98) и табл. П. З, получим

/ 5,75—5,0 Рп = Ф°( 0,25 ) + Ф°

 

= 0,998650 4- 0,998650— 1 = 0,997300.

Таким образом, если в процессе p(t) можно найти опасное или расчетное се­чение, в котором выход реализаций за установленные пределы наиболее опасен (и данном случае сужен интервал работоспособных состояний с каждой стороны на Ор), то вероятность параметрической безотказности будет значительно ниже и этом сечении (0,997300 вместо 0,999937) и при этом можно не учитывать длитель­ность и другие характеристики процесса.

Пример 2.4. Пусть работоспособность двигателя определяется одним нор­мально распределенным параметром —давлением в камере р с характеристиками и,, = 5 МПа, ар = 0,25 МПа. Выход этого параметра за пределы рп = 4МПа и /»в = 6 МПа рассматривается как отказ. При этом пределы рн и рй измеряются с ошибками 6р 8Рв (точность срабатывания реле давления), имеющими нормаль­ное распределение с математическими ожиданиями, равными нулю, н ар = —Орв =0,15 МПа. Найти вероятность того, что будет зафиксирован параметри­ческий отказ, если случайные величины р, 6Рн> 8рв независимы.

В данном случае задача заключается в определении вероятности выхода случайной величины р за случайные пределы рн и рв, имеющие нормальное рас­пределение с характеристиками тРн = 4 МПа; тРв = 6 МПа; аРн = аРв = = 0,15 МПа.

t

Найдем коэффициент корреляции р случайных величин Ун = р — рн и YB = Рв—Р> используя зависимость (2.83):

Р = -4/V (аР+сди)(арв+°1) =

= — 0,252// (0,252 + 0,152) (0,152 + 0,252)" = — 0,7356.

Поскольку коэффициент корреляции случайных величин Нн и Ув достаточно велик и им пренебречь нельзя, то разложим систему двух коррелированных нормально распределенных величин на систему Y’„, F’B с некоррелированными составляющими. Для этого используем зависимости (2.89) — (2.91). Средние квадратические отклонения вую <зУв величин Ун и Кв в соответствии с (2.78) и (2.79) можно найти в виде

°Ун = V °р+ °рн = У 0,252 + 0,152 = 0,29155;

°Ув = V арв + 4 = /0,152 + 0,252 = 0,29155.

Составим уравнение (2.91) для определения параметра я, который необходим при вычислении дисперсий случайных величин F’„, К’в:

tg2a = —24/(/_/).

Подставляя значения сгр, 0Рн> стРв; получим

tg 2а = — 2 • 0,252/(0,291552 — 0.291552).

Так как дисперсии ^гуп и сг2^ равны, а числитель выражения отрицателен, то а = —45°. С учетом этого, используя (2.90), найдем дисперсии случайных величин К’н и К’„:

=0,291552 [cos (— 45°)]2 — 0.252 sin 2 (— 45°) + 0.291552 [sin (— 45е)]2 ;

а’2 = 0.291552 [sin (— 45е)]2 + 0,252 sin 2 (— 45е) + 0.291552 [cos (— 45е)]2,

Ув

так как sin(—а) = —sina и cos(—а) = cosa, то

о ‘* = 0.291552 cos2 45° + 0.252 sin 90е + 0.29I552 sin2 45° = ун

= 0.291552 (/2~/ 2)2 + 0,252 ■ 1 + 0,29155 (/2~/ 2)2 = 0,147500;

о’ =0,38400; о’2 = 0.291552 sin2 45° — 0,252 sin 90° + 0,29155 cos2 45е =

% ув

= 0,022500; о’ =0,15000.

^в

Вероятность параметрической безотказности двигателя в соответствии с полученными результатами, зависимостью (2.92) и при использовании табл. П. 3 можно рассчитать в виде

Р„ = Ф0 Ф0 [,п’Уп / a’J = Ф0 (1,0/0,38400) Ф (1,0/0,15000) =

= Ф0 (2,004) Ф0 (6,607) = 0,995387 ■ 1 = 0,995387.

Условия примеров 2.2 и 2.4 отличались только тем, что в примере 2.4 были введены случайные нижний и верхний пределы, выход давления за которые при­водил к отказу двигателя. За счет дополнительных случайных факторов (ср. рис. 2.7 и 2.10) вероятность параметрической безотказности снизилась с 0,999937 до 0,995387.

Пример 2.5. В условиях примера 2.4 рассчитать вероятность параметри­ческой безотказности двигателя, если ошибка в работе реле, измеряющего верх­ний предел давления, отсутствует, т. е. оРв — 0.

В соответствии с (2.64), (2.65), (2.78) и (2.79) найдем математические ожида­ния и средние квадратические отклонения случайных величин VH и Y

т = т — т = 5,0 — 4,0 = 1,0 МПа; т = рв — тр = 6,0— 5,0 =

У н и Рн У в

= 1,0 МПа; о = ЛГ oi + о2 = V0,252 + 0,152 = 0,29155 МПа;

Ун г ‘ Р н

о = Г о2 + g2 = V О2 + 0,252= 0,25 МПа.

У В г гВ Р

По (2.83) рассчитаем коэффициент корреляции случайных величин Кн и Ув:

р = — о2/(° о ) = —0,252/(0,29155 ■ 0,25У= — 0,8576. р х Ун У в’

Приведем случайные коррелированные величины Кн и YB к некоррелиро­ванным YH’ и Y’в. В соответствии с (2.91) имеем уравнение для определения па­раметра я:

tg2* = — 2<т2/( а2 —о2 ) = — 2 — 0,252/(0,291552 — 0,252) = — 5,5556.

Р1 ‘ Ун Ув ‘

Так как <+„><*1, ир < 0, то угол я лежит в IV квадранте. Отсюда 2я =

. arctg(—5,5556); 2я = —79°47,8′; я = —39°53,9′

По (2.90) найдем средние квадратические отклонения п’ун, с ув некорре­лированных случайных величин FH, Кв:

а = □ cos2 а + /С sin 2зс + <т sin2 я = 0.291552 cos2 (—39°53,9′) —

Ун Ун Уз

— 0,252 sin (2 (— 39’53,9′)] + 0.252 sin2 (— 39°53,9′) =

= 0.291552 cos2 39’53,9′ +0,252 sin 7947,8′ + 0,252sin2 39°53,9′ =

= 0,291552 (0,7677)2Н-0,252 ■ 0,9842 + 0.252 (0,6408)2 =

= 0,08500 ■ 0,5894 + 0,0625 • 0,9842 + 0,0625 ■ 0,4106 да 0,137254;

а’ я; 0,3705; с’8 = 0,291552 sin2 (— 39°53,9′) + 0,252 sin (2 (— 39°53,9′)] +

Ун Ув

+ 0,25 cos2 (—39°53,9′) =0,08500 • 0,4106 — 0,0625 • 0,9842 +

+ 0,0625 — 0,5894 = 0,010226; ст’ =0,1011.

У а

Вероятность параметрической безотказности двигателя в соответствии с полученными результатами, зависимостью (2.92) и при использовании табл. П. З можно рассчитать в виде

Рп = Фо (rnyJ ojj Ф0 (т / o^J =ф0 (1,0/0,3705) Ф0 (1,0/0,1011) =

= Ф0 (2,699) Ф0(9,899) = 0,996521 • 1 = 0,996521.

Таким образом, за счет отсутствия ошибок при определении верхнего пре­дела работоспособного состояния величина Рп по сравнению с результатами примера 2.4 увеличилась от 0,995387 до 0,996521.

Пример 2.6. В условиях примера 2.4 рассчитать вероятность параметри­ческой безотказности двигателя при условии, что отказ наступает лишь при выходе давления за нижний случайный предел.

В соответствии с условиями задачи и зависимостью (2.93)

Рп = вер (Fн > 0) = Ф0 (myJ of/J = Ф0 (1,0/0,29155) =

= Ф0 (3,430) = 0,999694.

Пример 2.7. В условиях примера 2.6 рассчитать вероятность параметри­ческой безотказности двигателя, если отказ наступает лишь при выходе давления за неслучайный нижний предел рн = 4 МПа.

В соответствии с условиями и зависимостью (2.100)

Рп = Фо [(«V — Ртд/^р] = Фо [(5,0 — 4,0)/0,25] = Ф0 (4) = 0,999968.

Таким образом, приведенные выше зависимости и примеры показы­вают возможности управления значением вероятности параметриче­ской безотказности элемента за счет выбора или варьирования пара­метров, определяющих работоспособное состояние; вероятностных характеристик этих параметров; характеристик пределов, ограничи­вающих область работоспособных состояний элемента.

В инженерной практике часто без должных оснований пренебрегают вероятностными расчетами показателей надежности, используя не­которые постоянные коэффициенты (например, коэффициенты запаса прочности и т. п.), учитывающие возможные разбросы параметров элемента. В результате таких детерминированных расчетов можно получить два значения (1 или 0), определяющие работоспособность или неработоспособность элемента. Расчет вероятности параметрической безотказности приводит к определению любого значения от 0 до 1, характеризующего количественно надежность объекта, а главное — позволяет направленно выбирать режимы и условия работы объекта, при которых его показатели надежности достаточно высоки. Однако ясно, что для проведения таких углубленных расчетов нужна и дополнительная исходная информация о законах распределения или числовых характеристиках параметров элемента и пределов, опре­деляющих его работоспособное состояние.