ПОКАЗАТЕЛИ НАДЕЖНОСТИ СИСТЕМЫ

Такие сложные объекты, как Л А или ЛК, состоящие из тысяч деталей, узлов и сборок, обычно при расче­те показателей надежности рассматривают как системы. Из определе­ния понятия системы, используемого в теории надежности (см. § 2.1), следует, что в ней определены связи между элементами или структура системы, а также заданы показатели надежности элементов.

Таким образом, система является моделью реального объекта, соз­даваемой для расчета показателей его надежности. Для построения такой модели необходимо проанализировать режимы работы объекта и для каждого из них получить свою модель. Так, например, для ЛК можно рассматривать показатели надежности в состоянии готовности к пуску, при подготовке и проведении пуска, при движении ЛА по траектории. В каждом из перечисленных режимов функционируют различные агрегаты и приборы ЛК, а также отличны условия их функ­ционирования. Модель объекта, применяемую для расчета показате­лей его надежности при известных характеристиках составляющих его элементов, называют структурной схемой надежности (ССН). Для по­строения ССН обычно используют схемы функционирования объекта в различных режимах, т. е. функциональные схемы.

Примером функциональных схем для ЛА могут служить пневмо — гидравлические схемы, отражающие работу пневматических и гидрав­лических магистралей, связывающих двигатели, баки, системы надду­ва и заправки и т. п., а также различные электрические схемы. Струк­
турные схемы надежности значительно отличаются от функциональ­ных, связи между элементами в них проще. Следует также отметить, что число элементов в ССН зависит от состава исходных данных. На­пример, ЛК можно представить ССН, включающей в себя только не­сколько составных частей (ЛА, наземное оборудование, систему средств связи и т. п.), а любой составляющий элемент комплекса мо­жет иметь ССН, включающую десятки элементов.

Таким образом, задача описания объекта в виде системы для расче­та показателей его надежности заключается в построении ССН.

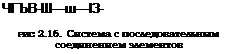Простейшей системой или ССН объекта является система (схема) с последовательным соединением элементов. При этом полагают, что число k элементов, образую­щих систему, конечно, а от­каз одного элемента ведет к отказу системы. Структурная схема надежности, описываю­щая такой объект, представ­лена на рис. 2.16. При рас­чете показателей надежности такой рассматриваемой системы обычно вводят довольно силь­ное допущение о том, что все отказы независимы; при этом расчеты показателей надежности системы заметно упрощаются.

Рассмотрим случай, когда все элементы системы с последователь­ным соединением в сформулированных выше условиях работают до первого отказа. С учетом независимости возникновения отказов ве­роятность безотказной работы системы в течение времени t

P(t) = UPi(t), (2.137)

і= і

где Pi(t) — вероятность безотказной работы за время t для t-ro элемента.

Так как в соответствии с (2.7) Рід) — 1 —Qi(t), то с учетом (2.137) получим

Q(/) = 1 —/>(0 =1 — П[1 —Q, (/)]. (2.138)

1=1

Если Q(t) <С 0,1, то (2.138) может быть упрощено разложением в ряд до линейных членов

<2(0« І<2|(0; Р(0~ і;- 2 Qi(0- (2-139)

£=1 i—l

Погрешность формулы (2.139) всегда положительная, так как

к k

1 — П [1 —Q* (/)] <; 2 Qi(t), причем величина ошибок не превосходит

£=1 (=1

к

O.5I2XM018- Если для элементов известны интенсивности отказов

1=1

Х,(/), то в соответствии с (2.14) и (2.137) имеем
(2.140)

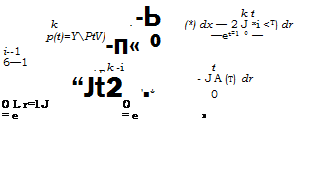где Л (т) — интенсивность отказов системы.

Таким образом, имеем

Л(т) = 2]Мт). (2.141)

Если все элементы имеют экспоненциальный закон (2.4), то Аг(т) = =^i и в соответствии с (2.141) и (2.140) получим

k

A = 2V, P(t) = e~At, (2.142)

і=і

т. e. закон возникновения отказов системы остается также экспонен­циальным.

Используя зависимость (2.20), связывающую среднее время жизни элемента Toi и интенсивность его отказов Kt при экспоненциальном за­коне, а также учитывая (2.142), найдем среднее время жизни или ма­тематическое ожидание времени работы системы до первого отказа:

Т’о-І/Л-і/Іх.-і/І 1/7V (2.143)

/ і=і / і=і

Если отказы элементов зависимы, то для вычисления показателей надежности системы необходимо знать совместный закон распределе­ния времени возникновения отказов всех элементов. Как правило, таких исходных данных не бывает, так как для их получения необхо­димо испытывать систему целиком; при этом, естественно, отпадает необходимость в расчете характеристик надежности системы через показатели элементов. В тех случаях, когда возникновение отказов элементов связано с изменением каких-либо общих внешних или внут­ренних условий их работы, целесообразно переходить к расчету па­раметрической безотказности методами, рассмотренными в § 2.3.

Для системы с последовательным соединением восстанавливаемых элементов удается так же легко рассчитать показатели надежности в том случае, когда процессы возникновения отказов и восстановлений для всех элементов независимы.

Если в этих условиях восстановление элементов полное и мгновен­ное, то случайная величина числа отказов системы r(t) к моменту времени t представляет собой сумму независимых случайных величин rt(t) числа отказов 1-го элемента к моменту t:

/•(*) = 2 М*). (2л44>

1

С учетом этого нетрудно найти функцию восстановления системы:

М [г(0J = О(0 = м[І г, (0І = Ім[Гі(0] = іG,(0, (2.145>

L«=i J i=i i=)

іде Q4(0 — функция восстановления t-ro элемента.

По определению (2.102) и с учетом (2.145) плотность восстановления системы

(2.146)

где юД/) — параметр потока отказов (плотность восстановления) і-го элемента.

В том случае, когда потоки отказов всех элементов подчиняются жспоненциальному закону с плотностью /,(/) = е—М и, следова­

тельно, параметр потока отказов t-ro элемента *>i(t) — со,- =. являет­ся постоянным (2.114), плотность восстановления и параметр потока отказов системы также постоянны:

k k

®(0.= 2 «і(0= 2 “г,

с = V t0| = ^ я,-; £1 (0 = urf. (2.147)

1=1 І— I

Если система включает большое количество независимых элемен­тов с мгновенным и полным восстановлением (число отказов каждого — элемента мало по сравнению с числом отказов системы), то в суммар­ном потоке практически отсутствует последействие и его можно счи­тать ординарным, т. е. поток отказов системы становится пуассонов — • ким. Тогда в соответствии с (2.112) и (2.113) вероятность получения ровно т отказов (восстановлений) системы за время t

Р [г (/) = т] = Рт (0 = e~S т , (2.148)

т!

P[r(f)<m]=2P*(*) = IS?

її вероятность получения в этих условиях не более т отказов

и, наконец, вероятность появления m отказов на интервале времени

п „ [Q«2)-Q (/ж)Г» 1*1» *2/—————- :

(/,. /2)

печное время, процессы отказов и восстановлений для всех элементов независимы и при восстановлении любого элемента вся система нера — — ботоспособна (выключены все элементы). При этом с момента восста­новления все элементы, кроме отказавшего, начинают работать так, как после мгновенного восстановления, а отказавший — как после восстановления за конечное время. Если время работы и восстановле­ния Его элемента имеют экспоненциальные распределения

Ft (t) = 1 — e~V ; G, (/) = 1 — e~|l*4 (2.151)

то в соответствии с (2.143) среднее время работы системы

Т,= 1/Л=: 1/211Ти, (2.152)

/ t=i

а среднее время восстановления системы

7’2=1/М=Г12№, (2,153)

і=і

где Л и М— параметры потоков отказов и восстановлений системы.

Коэффициент готовности системы может быть описан выражением (2.130), которое при принятых обозначениях имеет вид

KrV) = (м + Ле“(Л+М) ‘)/(М + Л), (2.154)

а стационарное значение коэффициента готовности системы на основа­нии (2.128) или (2.131) и с учетом (2.152), (2.153) определяется следую­щим образом:

Кт = м/(л + М) = ТАГ, + Т,) = т, j

= l/(l + 2 Тк/Т^У (2.155)

Для случая, когда во время восстановления одного элемента все остальные элементы системы продолжают работать, с учетом незави­симости потока отказов и восстановлений коэффициент готовности Ki(t) такой системы определяется произведением коэффициентов го­товности Kri{t) элементов:

Кг(0 = П Kri{t). (2.156)

В соответствии с (2.128) стационарное значение коэффициента готовности системы

/<г = П Та1(Ти + ТА — (2-157)

По (2.152) (см. [19]) среднее время работы системы

Tt =1/2 ити.

1=1

Одним из распространенных методов повышения надежности объек­та является резервирование. Чаще всего используют структурное ре­зервирование, предусматривающее использование избыточных элемен­тов в системе. Возможно также временное, информационное, функцио­нальное и нагрузочное резервирование (см. [241), при которых в систе­ме соответственно используют элементы с избыточным временем ра­боты, обрабатывают и используют избыточную информацию, приме­няют элементы, способные выполнять дополнительные функции или воспринимать дополнительные нагрузки.

Рассмотрим методы расчета показателен надежности систем со структурным резервированием. При таком виде резервирования раз­личают основной элемент, который необходим для функционирования системы, и резервные, обеспечивающие работоспособное состояние системы при отказе основного элемента. Отношение числа резервных элементов к числу резервируемых ими основных элементов называют кратностью резервирования. Резервирование^, кратность которого равна единице, называют дублированием.

Если резервные элементы находятся в том же режиме, что и основ­ной, то такой резерв считают нагруженным. Когда резервные элементы находятся в выключенном состоянии и до момента их включения из-за отказа основного или очередного резервного не могут потерять работо­способность, резерв называют ненагруженным. Различают также облегченный резерв, при котором резервные элементы находятся в ме­нее нагруженном режиме, чем основной элемент.

Резерв может быть восстанавливаемым или невосстанавливаемьш. Такое деление резерва определяется восстановлением или невосста- новлением резервных элементов после отказа. Различают также ре­зервирование с восстановлением или без восстановления. Если после отказа основного и резервных элементов следует восстановление, то имеет место резервирование с восстановлением. В том случае, когда ни основной, ни резервные элементы не восстанавливают, система имеет резервирование без восстановления.

Простейшая система со структурным резерви­рованием — система с параллельным соединением элементов. Например, имеется конечное число k элементов, составляющих нагруженный резерв (рис. 2.17). При отказе основного элемента (о) включается первый резервный, при отказе кото­рого начинает работать следующий резервный элемент, и т. д. При отказе всех элементов возни­кает отказ системы. Предполагают также, что пере­ключатель элементов абсолютно надежен.

Если резервирование не предполагает восста­новления, т. е. система работает до первого отказа н отказы всех элементов независимы (сильное до­пущение, которое далее будет проанализировано),

то вероятность Р(Н безотказной работы системы в Рнс‘ 2.17. Система. „ с параллельным

течение времени t определяется очевидной зависи — соединением эле-

bi остью ментов

Р(0= 1— п [1— Pt(f)], (2.159)

. t=02

где Pi(t) — вероятность безотказной работы за время t і-го (основного или резервного) элемента.

Если вероятности Pi(f) = P^(t) для всех элементов равны, то

P(t) = 1 — [1 — />t(f )]*н. (2.160)

При заданной надежности системы /р(/) с учетом зависимости (2.160) можно найти необходимое число Д’тр резервных элементов, при котором выполняется условие P(t) > Р;р (t):

К? р = £{1пН — PTP(f)]/ln[l — ЛШ, (2.161)

где Е(х) — целая часть х.

Если все элементы имеют экспоненциальный закон возникновения отказов

Ft(t)= l-e"V (і = 0, 1, 2,…, k), то в соответствии с (2.159) и (2.23) имеем

Р(/)= 1—П [1—Р,(*)]*= 1 — ri[l-eV|«l —

г=о »=о L J

-ГКМ)=1-^+1Пхг,

i=0 i=0

т. е. с погрешностью не более 0,5 П можно записать

& __________________

Р(0« 1— № п Х,= 1— Л/*+««е, (2.162)

/=о

к

где Л = П — интенсивность отказов системы.

i=0

Если все интенсивности отказов Я, г = то

Р(0«1— = 1— Atk+i = e-A<fc+’, (2.163)

где Л = .

Следовательно, для рассматриваемой системы при высокой на­дежности элементов получим распределение отказов близкое к распре­делению Вейбулла, если отказы элементов распределены экспо­ненциально. Заметим, что разложение в ряд (2.23) при параллельном соединении элементов в системе на практике не ведет к большим по­грешностям, так как надежность резервированной системы обычно вы­сокая: P(t) > 0,9.

В рассматриваемых условиях среднее время работы системы, имею­щей близкое к экспоненциальному распределение отказов в соответст­вии с (2.20) и (2.162), можно вычислить по приближенной зависимости

г0«і/л = і/п h-

I t=o

На основании (2.22) можно утверждать, что и среднее квадратиче­ское отклонение 0л времени до первого отказа системы определяется выражением (2.164), так как для экспоненциального распределения

Т0 = оа. (2.165)

Рассмотрим систему, состоящую из основного и k резервных эле­ментов (рис. 2.17), но с ненагруженным резервом. Будем полагать, что отказы элементов возникают независимо и время до отказа распреде­лено по экспоненциальным законам Ft = 1 —е—М (і = 0,1, 2, … …, k).

Можно показать 119], что в этом случае

П Ъ = 1 — Ло^ ~ Г**", (2.166)

k

где Л0 =—————— ПАі— интенсивность отказов системы с нена-

(*+ ■)1 і=0

груженным резервом.

Сравнивая (2.162) и (2.166), находим преимущества ненагруженно­го резерва по сравнению с нагруженным. При одинаковом количестве элементов в системе и одинаковых интенсивностях их отказов

п? J(*+1)! «п К — (2.167)

г=0 / г=гО

Заметим также, что в соответствии с (2.166) и (2.23) при высокой на­дежности элементов в этом случае распределение отказов системы так­же близко к распределению Вейбулла.

Вероятность безотказной работы системы при сформулированных выше условиях легко вычисляется и для случая, когда продолжитель­ности безотказной работы всех элементов распределены нормально с законами

где nit и сі — соответственно среднее время жизни и дисперсия време­ни жизни /-го элемента.

Случайное время жизни системы является суммой независимых нормально распределенных случайных величин жизни элементов

(2.169)

и распределено нормально с математическим ожиданием

(2.170)

т— V, т, i=о

и дисперсией

 

о2 = у of.

Jimmі і

£=0

Таким образом, закон распределения случайной величины времени жизни системы

где Ф0(х) — табличная функция (см. табл. П. З).

Для произвольного закона распределения времени жизни элемен­тов с учетом приближения (2.23) выражение (2.166) можно представить в виде

к

П П-/>;«)]

Р(/)^1— ———————— . (2.173)

В работе [191 доказано, что для многих произвольных законов рас­пределения времени жизни элементов выражение (2.173) дает хорошее приближение, несколько занижающее точное значение вероятности безотказной работы системы, состоящей из ненагруженного резерва, включающего в себя основной и k резервных элементов.

Облегченный резерв применяют в тех случаях, когда ненагружен — ный резерв не обеспечивает непрерывного функционирования системы. Обычно это связано с тем, что по природе элементов невозможно их мгновенное включение в работу при очередном отказе предыдущего (основного или резервного) элемента. Например, при отказе государ­ственной электросети ЛК может быть переведен на питание от дизель — генераторов, но их запуск и прогрев требуют определенного времени. Если дизель-генераторы могут длительное время работать на холостом ходу (в облегченном режиме), то возможен облегченный резерв в систе­ме энергоснабжения ЛК. Многие элементы электро — и радиоаппара­туры требуют времени для прогрева и выхода на рабочий режим, что также приводит иногда к необходимости создания облегченного резерва для повышения надежности работы аппаратуры без перерывов.

Рассмотрим систему, состоящую из одного основного и k резерв­ных элементов (рис. 2.17), в которой каждый элемент может функцио­нировать в рабочем и облегченном режимах. Пусть длительности рабо­ты в каждом из этих двух режимов для каждого элемента имеют экспо­ненциальные распределения:

Fw (t)= 1 — e-V ; F. об (0=1- e_>,: 06 ‘ ,

где Xjp и 7-і () R — интенсивности отказов і-го элемента в рабочем и об­легченном режимах.

Будем также полагать, что пребывание элемента в облегченном ре­жиме не влияет на время работы до отказа в рабочем режиме. Следует отметить, что это допущение достаточно сильное и на практике не всег­да выполнимо, однако при таком допущении все же учитывается зави­симость интенсивности отказов системы Лоб(/) не только от числа от­казов, происшедших ко времени t, но и от того, какие именно элементы отказали.

В сформулированных условиях вероятность безотказной работы P(t) системы в течение времени t может быть представлена приближен­ной зависимостью (см. [19]).

P(t)&l — tk+1 х

Таким образом, меняя последовательность работы элементов, при фиксированном их числе k и интенсивностях отказов Яір, Я10б можно повысить или понизить надежность системы. Будем полагать, что опти­мальным является такое размещение элементов, при котором надеж­ность системы максимальна, т. е. P(t) = шах. Это условие, как следует из (2-175), соответствует

П Очр + іЯіое) = min. (2.176)

t—о

Выражение (2.176) можно изменять, если имеющемуся набору кон­кретных пар значений (л;р, /.;об) придавать различные номера і = О, 1, 2, …, k. При этом за счет того, что коэффициент і перед вторым чле­ном выражения в скобках будет умножаться’на различные значения Яг-об, изменится и все произведение (2.176). Можно доказать непосред­ственной проверкой, что при выполнении условия

-?* < І2. < iffi. « … < (2.177)

^юб ^206 ^зоб об

обеспечивается минимум произведения (2.176). Действительно, в этом случае большие величины интенсивностей отказов будут умно­жаться на меньшие значения і, что даст и меньшее произведение.

Логические соображения также могут привести к этому широко известному результату. Если система включает в себя два элемента, у которых равны интенсивности отказов в облегченном режиме, то желательно, чтобы первым работал тот, у которого надежность в ра­бочем состоянии больше. Если у этих элементов равны интенсивности отказов в рабочем режиме, то желательно, чтобы элемент с меньшей надежностью в облегченном режиме первым был использован в рабо —

«чем режиме, так как, находясь в облегченном резерве длительное. время, он может с большей вероятностью отказать, чем второй элемент.

Для частного случая, когда интенсивности отказов всех элементов в каждом режиме одинаковы, т. е. >.if) = Яр и Агоб = >-оС, зависимости ї(2. 174) и (2.175) упрощаются:

Д(0=1-

__ fk+i ^-р Др + ^об) Др + 2ХоВ) … (Лр — f — г’Х0б) … (Хр — f — fe/рб) __

(ft — Ы) I ~~

= + <2178>

В рассмотренных выше схемах нагруженного, ненагруженного в облегченного резервов переключение элементов происходило с аб­солютной надежностью. На практике всякое устройство для переключения (переклю­чатель) имеет вероятность успешного срабатывания Дп < 1.

Рассмотрим возможности расчета надежности системы с нагруженным резервом и не абсолютно надежным пере­ключателем. Возможны два варианта системы:

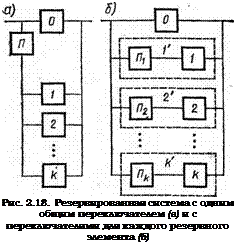
переключатель в системе один, и он последовательно включает резервные элемен­ты, причем при отказе основ­ного элемента и переключа­теля происходит отказ систе­мы (рис. 2.18, а);

каждый резервный элемент нмеетсвой переключатель; при отказе основного элемента, (k—1)-го резервного и k переключателей [(/г— —1)-го переключателя и /г резервных элементов] происходит отказ си­стемы (рис. 2.18, б). Для первого варианта при заданных вероятностях безотказной работы основного P0(t), і-го резервного Pt(t) элементов и переключателя Рп вероятность P(t) безотказной работы системы за время t может быть найдена по формуле полной вероятности (см. [12]). Введя упрощающую запись обозначений P(t) = Р; P0(t) = Р0 и Pi(t) = Pi, с учетом независимости отказов всех элементов и переклю­чателя получим

Р = Ро + (1 — Ро) Р. пРі + (1 — До) (1 — Pi) PnP2 + (1 — До) (1 — Pi) X X (1 — Д2) ДпДз+ • • • + (1 — До) (1 — Pi) (1 — Да) • . • (1 — Pk-i) ДпД* =

= Р0 + Рп(1 — Ро) [Pi + (1 — Pi) Рг +(1 — Л) (1 — Р*) Рз +•■■ +

+ (1 — РО (1 — Р2) … (1 — Р*_,) Рк] = Р0 +

+ Рп(1 —Р0)^Рг 0 (1 — Р])- (2-179)

(=1 /==і

Для случая Р( = Pj, когда надежности резервных элементов оди­наковы, (2.179) упрощается:

[Р = Р0 + Рп(1 — Ро) [Pt + Р, (1 — Pi) +

+ Рі(1-Рі)2+— + РД1-Р/-1]. (2.180)

Нетрудно заметить, что выражение в квадратных скобках пред­ставляет собой убывающую геометрическую прогрессию со знамена­телем (1 — Pi)< 1. Сумма членов такой прогрессии вычисляется по известной формуле из [261: *’

Pi + Pi(l — Pi) + Pi(l — Pi)2 + … + Pi(l — Pi)*-1 = 1 — — (1 — Pi)ft. (2.181)

Выражение (2.180) с учетом (2.181) принимает вид

P = Ро + P„(l — Ро)П — (1 — Pi)*!- (2.182)

Для второго варианта схемы (рис. 2.18, б) в предположении, что переключатели и резервные элементы отказывают независимо, можно найти надежности Р4- подсистем, состоящих из последовательно соеди­ненных переключателя с надежностью Pni и резервного элемента с надежностью Pt (на рис. 2.18, б показаны пунктирной линией). В соот­ветствии с (2.137) имеем

P’i = PruPi. (2.183)

Таким образом, далее можно рассматривать систему с абсолютно надежным переключателем и с нагруженным резервом, включающим k элементов с надежностями Р* (і = 1, 2, .., /г). На основании формулы полной вероятности вычислим надежность такой системы:

Р = Р0 + (1 — Р0)Рр, (2.184)

где Рр — надежность резерва из k элементов.

По зависимости (2.159) получим

Рр= 1-П 0-Pi). (2.185)

Подставляя (2.185) в (2.184), с учетом (2.183) имеем

р = рс+(і-рс)Гі-гі (i-prep4) .

г

Если надежности всех резервных элементов Р{ = РщРі = Р\Р = = Рь то (2.186) упрощается:

Р = Р0 + (1 — Р0)[1 — (1 — PnPf)kl (2.187)

Сравним формулы (2.182) и (2.187), определяющие надежность систем, представленных на рис. 2.18. Для этого найдем предельные надежности систем при /е-> оо, т. е. когда число резервных элементов растет неограниченно:

lim {Р0 + Рп (1 — Р0) [1 -0 — Л)*1} = Ро 4- Ри (1 — Р0) < 1; ]

(2.188)

Hm {Р0 + (1 — Р0) [1 — (1 — РпРіП} = Ро + (1 ~ Ро) = 1 ■

fc-»oo ;

Из полученного результата следует, что при любой надежности элементов и переключателей в схеме, приведенной на рис. 2.18, б, можно получить неограниченно высокую надежность, увеличивая чис­ло резервных элементов и переключателей. Для системы с общим пе­реключателем такая возможность отсутствует, причем при недостаточ­но высокой надежности переключателя введение дополнительных ре­зервных элементов практически не повышает надежности системы.

Для систем с ненагруженным резервом и не абсолютно надежными переключателями можно получить расчетные формулы для определе­ния вероятности безотказной работы, использовав приемы, описанные выше, однако зависимости для таких схем достаточно громоздки. Приведенные .методы расчета относились к доволь­но простым системам, в которых ре­зервировался один элемент. Если в системе резервируются отдельные элементы или их группы, то такое резервирование называют раздельным, а если резервируется объект в це­лом, то говорят об общем резервиро­вании.

Доказано, что увеличение мас­штаба резервирования при прочих равных условиях уменьшает надеж­ность системы. Сравним надежность двух систем. Пусть первая система (рис. 2.19, а) состоит из п последова­тельно соединенных элементов (І =1, 2, .., п), каждый из которых имеет нагруженный или ненагруженный ре­зерв ИЗ ih элементов (ij =t’i, iz, ‘., tfe). Вторая система составлена из тех же самых элементов, но масштаб резерва увеличен (рис. 2.19,6). При этом це-

почка из п основных элементов резервируется k цепочками, состав­ленными из последовательно соединенных резервных элементов. Для упрощения выкладок будем считать, что все элементы схемы отказы­вают независимо, причем вероятности Pa(t) = Pji(t) = Рп безотказ­ной работы произвольного элемента ij(jt) в течение времени і из­вестны.

При нагруженном резерве для первой схемы (рис. 2.19, а) надеж­ность 1-й подсистемы, включающей в себя to-й основной и ih резерв­ных элементов, в соответствии с (2.159) может быть вычислена по зави — , ft

СИМОСТИ Р =1 —П (1 ———— Ру).

i=0

Тогда надежность всей системы, включающей п подобных элемен­тов, соединенных последовательно, определяется выражением (2.137):

Если надежности всех элементов равны, т. е. Pi} = Рь то (2.189) упрощается:

Р = Г1 —(1 —Ч".

Для второй схемы (рис. 2.19, б) сначала найдем надежность /-й подсистемы, включающей в себя k последовательно соединенных эле.

П

ментов. В соответствии с (2.137) имеем Р/ = Пр^. Надежность всей

Если Pij = Pi, то (2.193) упрощается: 1 „ г, *+П"

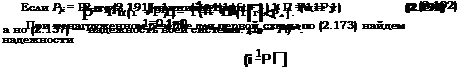системы можно найти как надежность k + 1 параллельно соединенных элементов с надежностями Р/. В соответствии с (2.159) получим

Для второй схемы надежность /-й подсистемы остается такой же,

П

как и для нагруженного резерва, т. е. Pi = I ІРуг, а с учетом (2.173)

(* — ь 1) ! ;=о ‘ " ■ (*+!)! Если Pji = Рj, то (2.195) принимает вид р»!————— !— (1-Р5)Н1 №+1)1

i=i

Для конечных п и k, а также при 0< Pij <-1 сравнение зависимо­стей (2.189) и (2.191) (нагруженный резерв) или (2.193) и (2.195) (не — нагруженный резерв) показывает заметные преимущества первой схе­мы.

Пример 2.22. Рассчитать надежности систем, структурные схемы которых представлены на рис. 2.19, а, б, для случая нагруженного и ненагруженного резерва при k = 3, п = 2 и P-tj = Pji = Pi = 0,8, если все элементы обеих схем отказывают независимо.

Для первой схемы при нагруженном резерве по зависимости (2.190) нахо­дим Р = [1 — (1 — 0,8)3+1]2 = 0,996803.

Для второй схемы при нагруженном резерве по формуле (2.192) получим Р = 1 — (1 — 0,82)3+l = 0,983204.

Для первой схемы при нагруженном резерве в соответствии с (2.194) имеем

Р ъ [і ———— 1—— (1 — 0,8)3+1Т = 0,999866.

L (3+1)1 1 J

Для второй схемы по (2.196) надежность

Р ^ 1 — ————— (1 — 0,82)3+1 = 0,999300.

(3+!)! ‘

Полученные результаты отражают преимущества первой схемы, а также еще раз подтверждают высокую надежность систем с ненагруженным резервом.

Рассмотрим еще один вид резервирования, называемый скользящим. При такой схеме группа или один резервный элемент может заменить любой отказавший основной элемент. Найдем показатели надежности системы, в которой использовано скользящее резервирование. Пусть система включает в себя п(і — 1,2, …, п) последовательно соединен­ных основных и k(j = 1,2,.., k) резервных элементов, каждый из ко­торых может заменить любой из п основных элементов. Будем пола­гать, что отказы всех п + k элементов возникают независимо, причем вероятности безотказной работы в течение времени t всех элементов одинаковы (Pi(t) = Pj(t) = Pi).

Для случая, когда скользящее резервирование выполнено k нагру­женными резервными элементами, вероятность Р безотказной работы системы равна вероятности того, что откажет не более к элементов из общего количества п + /г, т. е. вероятность Р определяется биноми­альным распределением (см. табл. П.1):

p=’kcUkpT 5 о +p>y — (2Л97)

s—О

Если распределение отказов каждого элемента имеет экспоненциаль­ный закон

F(t) = 1 — e~v; Pi (t) = = е~м, (2.198)

то зависимость (2.197) принимает вид

Р = J] C*+ft е~(n+fe_s) Kt (1 — e~M)s. (2.199)

s=0

Найдем среднее время Т0 работы системы до первого отказа. На интервале времени(0, /) до первого отказа работают п + k элементов, а вероятность того, что на малом участке At этого интервала не откажет элемент, равна е—:М*, тогда вероятность того, что не откажет ни один из п + k элементов, равна e~Xi(n+fc)A*.

Таким образом, до первого отказа интенсивность отказов Л(і) = = (п + к)"/.й на участке между первым и вторым отказами работает п + k ■— 1 элементов, т. е. к(2) = (п + к — 1)Я,; для произвольного участка Я(5) = (п k — s)Xt. В рассматриваемых условиях среднее время жизни системы

р _ *_____ і________ |_____ і_________ !________ і

0 ХДя + Аі) ^(n + k—l) lj(n + k — 2)

Для случая, когда скользящее резервирование выполено при не — нагруженном резерве, отказы элементов независимы и имеют экспо — ненциачьное распределение (2.198), вероятность безотказной работы системы в течение времени /, т. е. вероятность отказа за это время не более k элементов, определяется в соответствии с (2.115) зависимостью

р = 4 ОМ! е_лМ So 5 ‘•

где гікі — интенсивность отказа системы.

Среднее время жизни системы, т. е. математическое ожидание вре­мени наступления (/г + 1)-го отказа, определяется очевидной зависи­мостью

То = (k + 1 )Цпкі). (2.202)

Для скользящего резервирования характерно важное свойство: с увеличением масштаба резервирования надежность системы растет

как при нагруженном, так и ненагруженнсм резервах. Поясним это свойство анализом двух схем. Пусть первая система (рис. 2.20, а) состоит из г последовательно соединенных подсистем (і = 1, 2, .., г), и каждой из которых имеется л, последовательно соединенных элемен­
тов, a k[ элементов образуют группу, обеспечивающую скользящее резервирование в і-й подсистеме. Вторая система (рис. 2.20, б) вклю­чает в себя

л[3] = 2”* (2-203)

г=і

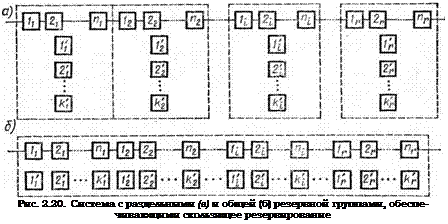последовательно соединенных основных элементов, а также общую резервную группу, обеспечивающую скользящее резервирование лю-

бого из последовательно соединенных основных элементов. В резерв­ной группе

а надежность системы, состоящей из г последовательно соединенных подсистем, на основании (2.137) будет

Для второй схемы по (2.203) имеем т последовательно соединен­ных элементов и по (2.204) — резервную группу из k& элементов, обеспечивающую скользящее резервирование. В этих условиях для расчета надежности системы можно использовать формулу (2.197):

Р * 2 <СК + *е ^S (1 — РіУ • (2.207)

s=0

Р0*>п дс ; 1=1 s=0 1 *

( Нетрудно показать, что для любых 0< Р < 1, конечных k’t и я,- выполняется неравенство

(2.208)

Г Гг

где Пъ = 2 п1; = 2

і=і 1=1

Для ненагруженного резерва при скользящем резервировании мож­но получить аналогичными методами расчетные зависимости для опре­деления надежности систем, представленных на рис. 2.20, а, б. Для этого необходимо дополнительно ввести допущение об экспоненциаль — ности распределения времени жизни элементов, что позволит исполь­зовать формулу (2.201).

—n. X,< e * »

Для первой схемы (рис. 2.20, а) вероятность безотказной работы t-й подсистемы в течение времени t

где 7і — интенсивность отказов любого элемента.

В соотеєтстеии с (2.137) надежность есєй системы

Для второй схемы (рис. 2.20, б) на основании (2.201) надежность

Для ненагруженного резерва при 0< оо, конечных пг и kt также имеет место неравенство

Следует отметить, что при скользящем резервировании выигрыш в надежности системы по сравнению с раздельным или общим ре­зервированием уменьшается, если учесть ненадежность переключа­телей. Это связано с тем, что при скользящем резервировании нуж­но иметь возможность каждый элемент резервной группы включать вместо любого отказавшего основного элемента.

Проиллюстрируем возможности расчета показателей надежности систем с использованием полученных выше или приведенных по лите­ратурным данным точных и приближенных формул.

Пример 2.23. Рассчитать надежность схем со скользящим резервированием, представленных на рис. 2.20, а, б, при условии, что г — 2; пх — Пц = 1; 6, = = k2 — I; надежность всех элементов = 0,8, отказы всех элементов наступа­ют независимо, резерв нагруженный.

Для схемы, представленной на рис. 2.20, а, в соответствии с (2.205) и усло­виями задачи рассчитаем надежность одной подсистемы:

1 21 Pi = У С®0,82-* (1 — 0,8)* = 0,82 + —0,8 (1 — 0,8) = s=o 11 1 !

= 0,64 + 0,32 = 0,96.

Так как обе подсистемы имеют одинаковую надежность, то Р = Я? = = 0,962 = 0,9216.

Используя зависимости (2.203), (2.204) и (2.207), получим:

2 2

fii = 2, ~ 2,

l=i «’=і

2 4 і

Я = 2 C’0,84-*(l— 0,8)* = 0.84+ —— 0,83 0,2 +

s=0 1 ‘ ^ ‘

+ 0,82 • 0,22 = 0,4096 + 0,4096 + 0,1536 = 0,9728.

Пример 2.24. В условиях примера 2.23 рассчитать вероятность безотказной работы в течение t = 1000 ч систем, схемы которых представлены на рис. 2.20, а, б, если законы распределения времени жизни элементов экспоненциальные с — 0,2232 • 10’3 ч+

(1 . 0,2232 ■ КГ8 — 103)* s 1

—1-0,2232-10-*.10* Є

Для схемы, представленной на рис. 2.20, а, найдем надежность і-й подсис­темы в соответствии с (2.209), используя табл. П-7:

_ у 0.9756

s=0 s ^

а также надежность всей системы, состоящей из двух одинаковых подсистем, P(t) = 0.97562 « 0,9518.

Для схемы, представленной на рис. 2.20, б, в соответствии с (2.203), (2.204) и (2.211) найдем вероятность безотказной работы в течение 1000 ч, используя табл. П.7:

2 _ 2

= 2 h = 2= ч = 2 ч — 2;

i=i i=i

Заметим, что в этом примере была выбрана интенсивность отказов такая, чтобы вероятность безотказной работы элементов в течение 1000 ч составила 0,8 (е—о,2232-іо-*-іо» = 0,8). Таким образом, можно», сравнить результаты рас­четов в примерах 2.23 и 2.24. Анализ этих данных показывает преимущества вто­рой схемы (рис. 2.20, б), а также высокую надежность схем с ненагруженным ре­зервом.

Пример 2.25. Рассчитать вероятность Р безотказной работы в течение одного года системы, включающей в себя три последовательно соединенных элемента, работающих до первого отказа с равными вероятностями отказа в течение одного года; <2х = 0,01.

з

По (2.137) имеем Р = П (1 — 0,01) = 0,993 = 0,970299, или по (2.139) 1=1

Пример 2.26. Найти вероятность Р безотказной работы в течение одного года и среднее время жизни Т0 системы, включающей три последовательно сое­диненных элемента, работающих до первого отказа и имеющих экспоненциальное распределение времени жизни с одинаковыми интенсивностями отказов = = 10-° ч-1.

По (2.142) найдем интенсивность отказов системы: А = 3 • 10 6 ч-1 и ве­

роятность безотказной работы в течение одного года (8760 ч):

—3-10-‘-8760 —0,02628

Р = е = е

В соответствии с (2.143) имеем Т0 = 1/(3- 10“°) = 10°/Зч= 10°/(3 X X 8760) « 38,05 года.

Пример 2.27. Найти вероятность P[r(i) < 2] того, что система из 30 после­довательно соединенных элементов откажет не более двух раз в течение года, если каждый элемент мгновенно и полностью восстанавливается, а параметры потока отказов для всех элементов равны coj = 10_6 ч-1.

В соответствии с (2.147) плотность восстановления системы со = 30(Oj = 30 • 10"° ч-1. а для t = 8780 ч функция восстановления системы Q (<) = 30 • 10"* • 8760 = 0,2628.

Так как число элементов в системе достаточно велико, то можно считать поток отказов пуассоновским и использовать формулу (2.149). По таблице П.7 кванти­лей распределения Пуассона, интерполируя, найдем

Пример 2.28. Найти коэффициент готовности через 30 сут (т. е. 720 ч) ра­боты для системы с тремя последовательно соединенными элементами, имеющей независимые и одинаковые для всех элементов экспоненциальные законы време­ни жизни элемента с Тц = Ю4 ч и времени восстановления с Т2і = 50 ч, если при восстановлении любого элемента все остальные не работают и система в это время не работоспособна. *

По (2.152) и (2.153) найдем параметры потоков отказов и восстановлений^сис- темы:

_________ 1_________

U/(3.10-4)] • З • 50/104

В соответствии с (2.154) значение коэффициента готовности системы Кг (t = 720 ч) = (200,0 . 10-4 + 3 • 10- ^ ^+200,о.10-<> яоу(3 . ,0-4 +

+ 200,0 • 10-) = (200,0 ■ 10- + 3,00 • 10- е~ 14’62)/(203,0-10-) да 200,0/203,0 да 0,98522.

Таким образом, через 30 сут работы системы коэффициент готовности при­нимает стационарное значение, которое можно было бы вычислить и проще (2.155)1

/^,= 1/(1+ 3 • 50/104) = 0,98522.

Пример 2.29. Найти вероятность безотказной работы в течение 100 ч не — восстанавливаемой системы, включающей в себя один основной и два нагружен­ных резервных элемента, работающих независимо, если вероятность Pi безот­казной работы любого элемента в течение 100 ч равна 0,8.

По (2.159) имеем

Р = 1 _ (1 _ Pj)3 = і _ (і _ 0>8)? = о,992000.

Пример 2.30. В условиях примера 2.29 найти количество krp резервных элементов, при котором надежность системы будет не менее 0,999, если надеж­ность элемента Pi = 0,8.

В соответствии с (2.161) получим

krp = Е {1п(1 — 0,999)/1п(1 — 0,8)) = Е(4,292) = 4.

Пример 2.31. В условиях примера 2.29 найти вероятность безотказной ра­боты системы в течение 10000 ч и среднее время жизни, если все элементы име­ют экспоненциальное распределение времени жизни с интенсивностью Я-1 = = 10- ч1.

В соответствии с (2.163) найдем Р да 1 — (10 2)3 ■ 10 000 = 0,990000.

Так как Р(10 000 ч) =0,990, т. е. надежность системы высокая, то по (2.164) имеем

Т0 да 1/(10-)3 = 10е ч.

Пример 2.32. В условиях примера 2.29 найти вероятность безотказной работы системы, если резерв ненагруженный,

По (2.173) определим

Р% 1 — (1 — Р,)3/3 ! = 1 —(1 —0,8)3/6 = 0,998667.

Пример 2.33. В условиях примера (2.31) рассчитать надежность системы, если резерв ненагруженный.

На основании (2.166) получим

Р = 1 — 10 000(10~2)3/3! = 0,998337,

Пример 2.34. Для системы, состоящей из одного основного и двух резерв­ных элементов, работающих в основном режиме с Яр = 10’2 ч-1 и в облегченном с ^об = Ю’3 ч-1 при условии, что работа в облегченном режиме практически не влияет на отказы в основном режиме, найти вероятность безотказной работы в течение 100 ч.

По зависимости (2.178) имеем

„ ЮО3 — 10’2 (10-2 + 10-3) (10-2 _|_ 2 . 10-3) (10-2 — I — 3 • 10-3)

3 !

Пример 2.35. Найти надежность системы (см. рис. 2.18, с), включающей в себя один основной элемент с надежностью Рс = 0,8, от одного до пяти нагру­женных резервных с надежностью Рх = 0,8 и общий переключатель с надежно­стью срабатывания Ри = 0,9.

В соответствии с (2.182) получим

Р = 0,8 + 0,9(1 — 0,8)[1 — (1 — 0,8)*] =*0,8 + 0,18(1 — 0,2й).

Для k = 1, 2, 3, 4, 5 найдем значения Р = 0,944000; 0,972800; 0,978560; 0,979712; 0,979942. Наконец, при k -»- то значение Р= 0,980000. Следова­тельно, при сравнительно низкой надежности переключателя нецелесообразно вводить в систему большое количество резервных элементов (в условии задачи — больше трех-четырех).

Пример 2.36. Найти надежность системы (см. рис. 2.18, б), включающей в себя один основной элемент с надежностью Р0 = 0,8, от одного до пяти нагру­женных резервных элементов с надежностью Рх = 0,8, каждый из которых имеет свой переключатель с надежностью Рп = 0,9.

На основании (2.187) найдем

Р = 0,8 + (1 — 0,8)[1 — (1 — 0,9 • 0,8)*] = 0,8 + 0,2(1 — 0,28й).

Для k = 1, 2, 3, 4, 5 рассчитаем значения Р = 0,94400; 0,98432; 0,995610, 0,998771; 0,999656. При k -*■ оо значение Р— 1,000000. Таким образом, прн принятой схеме целесообразно увеличивать число резервных элементов, если требуется въюокая надежность системы.

Пример 2.37. Найти вероятность безотказной работы системы, состоящей из трех основных и двух нагруженных резервных элементов, если резервирова­ние скользящее, а надежность всех элементов Pj = 0,8.

В соответствии с (2.197) имеем

2 с |

Р=2 ф,85-5(1-0,8)* = 0,83+—— 0,8*. 0,2 +

s—0 1 1 41

5 !

+ — — 0,83.0,22 = 0,327680 + 0,40960 + 0,20480 = 0,94208.

— (5—slMO-MO4/, —2-ИГМО* s е (і-e ;

Пример 2.38. В условиях примера 2.37 найти вероятность безотказной работы и среднее время жизни в течение 100 ч системы, если все элементы имеют время жизни, распределенное по экспоненциальному закону с?^ = 2 • 10~3 ч_*. В соответствии с (2.199) вероятность безотказ