СТАТИСТИЧЕСКИЕ ОЦЕНКИ ПАРАМЕТРА ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ

Наиболее распространенным законом воз­никновения отказов изделий яеляєтся показательный или экспо­ненциальный (см. табл. П.1). Для неремонтируемых (невссстанаЕливае — мых) изделий параметр экспоненциального распределения принято обозначать X, а для ремонтируемых — оа. Далее для краткости изло­жения примем одно обозначение К для ремонтируемых и неремсктпруе — мых изделий.

До сих пор при определении оценок параметров распределений имели дело с выборками из бесконечной генеральной совокупности, полученными без каких-либо ограничений на условия их формирова­

ло

ния при независимых испытаниях. При определении оценок к важную роль играет принятый статистический план испытаний, включающий в себя условие окончания испытаний каждого образца и всей серии из­делий, а также возможность или невозможность замены отказавших образцов в ходе испытаний.

Различают следующие основные статистические планы независимых испытаний на надежность серии из п элементов: с заменой (восстанов­лением) отказавших элементов и прекращением испытаний в заданный момент времени Г [план (и, В, 7)1; с заменой отказавших элементов и прекращением испытаний после отказа заданного числа г элементов [план (п, В, /■)]; без замены отказавших элементов и с прекращением испытаний после отказа заданного числа г элементов [план (я, Б, г)]; без замены отказавших элементов и с прекращением испытаний в момент Т [план (я, Б, 7)1.

Кроме перечисленных выше планов применяются биномиальный, о котором речь шла выше, а также различные комбинированные планы, в которых для каждой группы элементов в серии могут назначаться свои условия окончания эксперимента.

Если генеральная совокупность конечна и выборка не возвраща­ется в совокупность (безвозвратная выборка), то можно использовать гипергеометрическое распределение вероятностей (см. табл. П. І, П. 12) и рассматривать этот случай как своеобразный план испыта­ний. Подробнее этот вопрос будет рассмотрен в § 5.7.

Применение того или иного плана приводит к своеобразному усе­чению (цензурированию) выборки, которое необходимо учитывать

• Л

при получении формул для расчета оценок к. Используя результаты, полученные в фундаментальном труде [191, а также их некоторое раз­витие автором в работе [17], запишем формулы для определения оце-

Л л

нок к, их дисперсий и односторонних верхних пределов >.)Б с коэффи­циентом доверия уі.

Для плана (я, В, Т) несмещенная оценка максимального правдо­подобия

к = т (7)/(я7), (5.49)

л

где т(Т) — общее число отказавших за время (0, 7) элементов из числа п поставленных на испытания.

Среднее квадратическое отклонение этой оценки

сг[х] =ах = V кЦпТ) « V к/{пТ) . (5.50)

Л Л

Оценка к линейно зависит от числа отказов т(7), которое как ред­кое событие распределено по закону Пуассона (5.14). Поэтому одно-

л

сторонний верхний доверительный предел к1в с коэффициентом до-

Л

исрия Yi Для оценки к (5.41) определяется выражением

л

где a4^Tl(m) —■ квантиль распределения Пуассона, определяемая по табл. П.7.

Квантили распределения Пуассона в соответствии с (5.14) находят­ся из уравнения

Л

е Vt,= 1-Vi* (5-52)

/г—О

Пример 3.10. Пусть в результате испытаний по плану (п, В, Т) в течение Т = 100 ч 50 изделий (п = 50), отказы которых подчиняются экспоненциальному

Л Л

закону, наблюдалось m = 5 отказов. Найти оценку Я, ее дисперсию и односторон­ний верхний доверительный Предел с коэффициентом доверия Yl = 0,95.

По (5.49) и (5.50) находим:

А = 5/(50 • 100) = 10~3 ч-1;

яг V 10~3/(50 • 100) * 0,447 — 10~3 ч1.

Л

По табл. П.7 при m = 5 находим квантиль ao, os(5) — 10,513 и по (5.51) имеем

А1В = 10,513/(50 ■ 100) ч=2,103 • 10~3 ч~1.

Для плана (п, В, г) несмещенная оценка параметра Я определя­ется по зависимости

Я = (7— )l(ntr) (г>1), (5.53)

Л

где t г — время наступления заданного заранее л-го отказа.

Среднее квадратическое отклонение этой оценки

о [я] = ах = Я /Vг — 2 лг Я /fг — 2, (5.54)

а односторонний верхний доверительный предел

L=a,_Ti(r-l)/(nt)- (5.55)

Пример 5.11. Пусть в результате испытаний по плану (л, В, г) 50 изделий

Л

(п = 50) до пятого отказа (/л = 5) зафиксировано время наступления этого от-

Л л

каза <5 = 100 ч. Найти оценку Я, ее дисперсию и односторонний верхний довери­тельный предел с коэффициентом доверия Yi = 0,95, если отказы элементов под­чиняются экспоненциальному закону.

По (5.53) и (5.54) находим:

Я= (5 — 1)/(50 ■ 100) =0,800 ■ Ю~3 ч-1;

<тх ча 0,800 • 10“3 / У5 — 2 « 0,462 • 10~3 ч *;

По табл. П.7 определяем ао,05(4) = 9,154. Тогда в соответствии с (5.55) по­лучим Л

Я1в = 9,154/(50 ■ 100) да 1,831 • 10^ ч-1.

Для плана (п, Б, г) несмещенная оценка параметра

Я = (г— 1)/S£(£r), (5.56)

л

где Бб^г) — суммарная наработка п элементов до заданного г-го отказа.

Величина суммарной наработки

SB(tr)= І fi + (n-r) /г, (5.57>

i=i

л

где ti — время наработки t’-ro отказавшего элемента.

Среднее квадратическое отклонение этой оценки определяется по

(5.54) , а односторонний верхний доверительней предел с коэффициен­том доверия Yi будет

Ч, = fl,_Tl(r- l)lSB(ir). (5.58)

Пример 5.12. Пусть в результате испытаний по плану (п, Б, г) 50 изделий (п = 50) до пятого отказа (г = 5) определены следующие моменты возникнове — л Л л л л

ния отказов: t1 = 19 ч, t2 — 43 ч, ta = 87 ч, t4 = 91 ч, t5 = 100 ч. Требуется най­ти оценку параметра Я, ее дисперсию и односторонний верхний доверительный предел с коэффициентом доверия ух = 0,95, если известно, что интенсивность отказов Я постоянна.

По (5.57) определяем суммарную наработку: Ss(tr) = 19+ 43 + 87 + 91 + + 100 + (50—5)100 = 4840 ч.

В соответствии с зависимостями (5.56) и (5.54) находим:

Я = (5 — 1)/4840 да 0,826 ■ 10~3 ч1;

с, да 0,826- 10~3 IY5 — 2 да 0,477- 10 3 ч-1.

По табл. П.7 при г — 1=5— 1=4 и 1 —yi=l — 0,95 = 0,05 находим 00,05(4) = 9,154 и по (5.50) имеем

Я1В =9,154/4840ч= 1,891 — 10~3 ч~+

Для плана (», Б, Т) обычно в литературе предлагается смещенная оценка максимального правдоподобия

k = m[T)/sB(T), (5.59)

л л

где ш(Т) — число отказов, наблюдаемых за время Т; Se (Т) — сумма р — иая наработка п элементов за время Т.

Величина суммарной наработки

л

m (Г)

W) = ^ Ъ + [п-т{Т) Т.

г5Г

Можно показать (см. [17]), что несмещенная оценка параметра Я при плане (п, Б, Т) имеет вид К = [т(Г> — 1 ]/Sfi(T) (m(T)> l). (5.61) Приближенное выражение для среднего квадратического отклоне- л ния оценки максимального правдоподобия Я записывают в виде

(5.63)

Л Л где Рih(Yi, ti, m(T)) — односторонний нижний доверительный предел оценки вероятности безотказной работы при биномиальном плане, определяемый по табл. П.10 или с использованием пуассоновского приближения [см. табл. П.7, выражения (5.41)—(5.43)], или по нор­мальному приближению [см. выражения (5.45) и (5.46)].

Пример 5.13. Пусть в результате испытаний по плану (я, Б, Т) 50 изделий Л (п = 50) в течение Т = 100 ч было зафиксировано m — 5 отказов, а суммарная л наработка составила Si;(T) = 4840 ч. Требуется найти оценку параметра Л, ее дисперсию и односторонний верхний доверительный предел с коэффициентом доверия у1 = 0,95, если известно, что интенсивность отказов Я постоянна. По (5.59) и (5.61) находим оценку максимального правдоподобия и несме­щенную оценку параметра Я: Я = 5/4840 « 1,033- Ю’8 ч"1; л0 = (5— 1)/4840 « 0,826 • 10"8 ч-1. В соответствии с (5.62) имеем ол « 1,033 • 1 (Гя/г5 « 0,462 • 10_3 ч-1. л Л л При ух = 0,95; п — m = 45 и m = 5 по табл. П. 10 находим Р1п = 0,801. При использовании пуассоновского приближения по табл. П. 7 находим «0,05(5) = 10,513, а по (5.43) получим Р1н = (2 • 50—5—10,513)/(2 • 50 — 5 + + 10,513) = 0,801. Для нормального приближения по (5.12) и (5.13) найдем: р= 1 —5/50 = 0,900; ар = V0.900 (1 — 0,900)/(50— I) « 0,043.

По (5.47) и (5.45) при «т, = 1,645 определим:

1 — 1,8/50 = 0,964; Рш = 0,964 (0,900 — 1,645 — 0,043) = 0,799.

^5о; 0.950

2,21 — 10~3 ч-1.

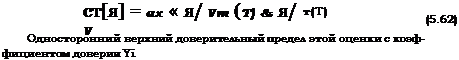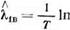
Для плана («, Б, Т) при наличии результатов неполных испытаний могут быть получены оценки параметра X, в которых учитывается вся опытная информация. Рассмотрим сначала, что представляют собой неполные испытания. При испытаниях по плану (п, Б, Т) часто возни­кает ситуация, при которой группа изделий работает безотказно, но

Л

в течение времени tj< T(j =1,2, …., пі). Например, при летных или стендовых испытаниях J1A из-за отказа системы управления, двигателя или другого агрегата испытание прекращается в случайный момент

л

tj. При этом ряд агрегатов и систем безотказно работали менее установ­ленного срока Т. Для этих агрегатов н систем данное испытание явля-

л

ется неполным, однако желательно учесть в оценке X дополнительную информацию, заключающуюся в том, что в неполных испытаниях изделие работало безотказно в течение каких-то случайных интервалов

Л

времени (0, tj).

Таким образом, после проведения п + щ испытаний статистиче-

л

ская информация представлена тремя группами данных: т{Т) отказов

л

в моменты времени tt ^ Т в ходе п полных испытаний; щ неполных

Л

испытаний, в которых изделия работали без отказа до моментов tj< Т;

Л

п — пг(Т) успешных испытаний при работе до момента Т.

Можно показать (см. [4, 17]), что оценка максимального правдопо­добия параметра X в этом случае должна рассчитываться по формуле

X=m(T)l %(Т) + ГДл], (5.64)

где А«1 — число дополнительных полных испытаний, эквивалентных неполным.

Величину Atii находят из следующих соображений. Составим отно­шение средней в щ испытаниях вероятности отказа на интервале (О, tj) к вероятности отказа на интервале (О, Т):

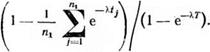(5.65)

Естественно считать, что при т] = 1 неполное испытание совпадает с полным (эквивалентно ему по информативности). Поэтому Дщ = = цщ. Обычно для достаточно надежных изделий XT< 0,1 и Ktj<Z0,l, что позволяет принять д

1 г ~ХІ і. Л

е ‘ я» 1 — XT и е » 1—X tj.

В этих условиях (5.65) упрощается:

(5.66)

ITS

Подставляем (5.66) в (5.64), после преобразований получим

к (Т) + 2 tjI = m (Т)ЦІБ (Т, /ц)], (5.67)

/=і J

л

где Se(T, пі) — суммарная наработка в п + /ц испытаниях.

Сравнивая (5.67) и (5.59), можно заметить, что они совпадают при Пі = 0 , что и следовало ожидать. Оценка (5.67), как и (5.59), является смещенной. Несмещенная оценка в этих условиях имеет вид, анало­гичный (5.61):

K=[m(T)~ i]/[s£(7 «,)] m(T)~> і]. (5.68)

Односторонний верхний доверительный предел оценок (5.67) и (5.68) приближенно можно рассчитывать по (5.63), полагая общее чис-

Л

ло испытаний, по которым находится величина Р1и, равным п 4- Ant. Приближенное значение среднего квадратического отклонения оце­нок (5.67) и (5.68) определяется по зависимости (5.62).

Пример 5.14. Пусть в ходе испытаний по плану (п, Б, Т) 50 изделий до

Л

времени Т = 100 ч наблюдалось m = 5 отказов и, кроме того, было щ = 13

Л

неполных испытаний. Суммарная наработка Sb (Т) = 4840 ч, а наработка в 13 неполных испытаниях составила 960 ч. Требуется найти оценку параметра X, ее дисперсию и односторонний верхний доверительный предел с коэффициентом доверия у, = 0,95, если интенсивность отказов постоянна.

По (5.68) и (5.62) находим: Я0 = (5 —1)/(4840 -|- 960) яг 0,690 • 1(Г3 ч-1; 0Х = 0,690 • 10~3/)/ 5 я; 0,309 ■ 10“3 ч-1.

В соответствии с (5.66) коэффициент г) = 960/(100 • 13) » 0,738, а величина Лпі = щч = 13 • 0,738 = 9,60.

Л л

При п — m — 50 |- 9,6 — 5 я? 55, ^ = 0,95, m = 5 по табл. П. 10 находим Л

Рт= 0 ,831, а по (5.63) рассчитываем

Л 1 1

А. „ = ——————— ІП——————-

1Е 100 0,831

Заметим, что условия примеров 5.13 и 5.14 совпадают при пг = 0, поэтому

уменьшение оценки Яі с 0,826 • 10’3 до 0,690 • 10~3 ч-1 и ее доверительного пре­дела с 2,21 • 10“3 до 1,85 • 10_3 ч-1 достигнуто только за счет учета информации неполных испытаний.